A vector field is considered spatially continuous if its magnitude and direction change smoothly with position, without any sudden variations or discontinuities.
Even though the electric field may be continuous in adjoining dissimilar media, it may well be discontinuous at the boundary between them. Boundary conditions specify how the components of fields tangential and normal to an interface between two media relate across the interface Here we derive a general set of boundary conditions for E, D, and J that is applicable at the interface between any two dissimilar media— be they two dielectrics or a conductor and a dielectric. Of course, any of the dielectrics may be free space. Even though these boundary conditions are derived assuming electrostatic conditions, they remain valid for time-varying electric fields as well.
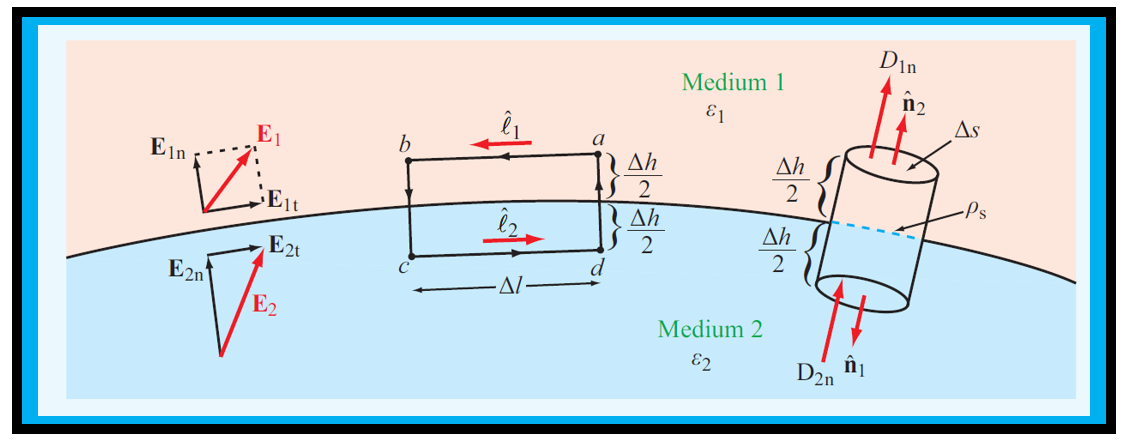
Above figureshows an interface between medium 1 with permittivity ε1 and medium 2 with permittivity
ε2. In the general case, the interface may contain a surface charge density s (unrelated to the dielectric polarization charge density). To derive the boundary conditions for the tangential components of E and D, we consider the closed rectangular loop abcda shown above and apply the conservative property
of the electric field expressed by Eq:
\[
\oint_C \mathbf{E} \cdot d\mathbf{l} = 0 \quad \text{(electrostatics)}
\]
which states that the line integral of the electrostatic field around a closed path is always zero. By letting Δh→0, the contributions to the line integral by segments bc and da vanish. Hence,
\[
\oint_C \mathbf{E} \cdot d\mathbf{l}
= \int_a^b \mathbf{E}_1 \cdot \hat{\ell}_1 \, dl
+ \int_c^d \mathbf{E}_2 \cdot \hat{\ell}_2 \, dl
= 0,
\]
where ˆℓ1 and ˆℓ2 are unit vectors along segments ab and cd andE1 and E2 are the electric fields in media 1 and 2. Next, we decompose E1 and E2 into components tangential and normal to the boundary.
$$
\mathbf{E}_1 = \mathbf{E}_{1t} + \mathbf{E}_{1n},
$$
$$
\mathbf{E}_2 = \mathbf{E}_{2t} + \mathbf{E}_{2n}.
$$
Noting that \( \hat{\ell}_1 = -\hat{\ell}_2 \), it follows that
$$
(\mathbf{E}_1 – \mathbf{E}_2) \cdot \hat{\ell}_1 = 0.
$$
In other words, the component of \( \mathbf{E}_1 \) along \( \hat{\ell}_1 \) equals that of \( \mathbf{E}_2 \)
along \( \hat{\ell}_1 \), for all \( \hat{\ell}_1 \) tangential to the boundary. Hence,
$$
\mathbf{E}_{1t} = \mathbf{E}_{2t} \quad (\text{V/m}).
$$
Thus, the tangential component of the electric field is continuous across the boundary between any two media.
Upon decomposing \( \mathbf{D}_1 \) and \( \mathbf{D}_2 \) into tangential and normal components (in the manner of Eq. (4.98)) and noting that
\( \mathbf{D}_{1t} = \varepsilon_1 \mathbf{E}_{1t} \) and
\( \mathbf{D}_{2t} = \varepsilon_2 \mathbf{E}_{2t} \),
the boundary condition on the tangential component of the electric flux density is
$$
\frac{\mathbf{D}_{1t}}{\varepsilon_1} = \frac{\mathbf{D}_{2t}}{\varepsilon_2}.
$$
Next, we apply Gauss’s law to determine the boundary condition on the normal components of \( \mathbf{E} \) and \( \mathbf{D} \).
Consider a small pillbox straddling the boundary with cross-sectional area \( \Delta S \) and vanishing height \( \Delta h \to 0 \).
The total outward flux of \( \mathbf{D} \) through the pillbox surfaces equals the charge enclosed.
The side flux tends to zero as \( \Delta h \to 0 \), so only the top and bottom faces contribute.
If \( \rho_s \) is the surface charge density on the boundary, the enclosed charge is \( Q = \rho_s \Delta S \). Hence,
$$
\oint_S \mathbf{D} \cdot d\mathbf{S}
= \int_{\text{top}} \mathbf{D}_1 \cdot \hat{n}_1 \, dS
+ \int_{\text{bottom}} \mathbf{D}_2 \cdot \hat{n}_2 \, dS
= \rho_s \Delta S.
$$
where ˆn1 and ˆn2 are the outward normal unit vectors of the bottom and top surfaces, respectively. It is important to remember that the normal unit vector at the surface of any medium is always defined to be in the outward direction away from that medium. Since ˆn1 = −ˆn2.