where you start learning everything about electrical engineering computing, electronics devices, mathematics, hardware devices and much more.
Linearly Independent Vectors: How to test the given vectors are linearly independent or not? The vectors v1,v2,v3,…vn in a vector space V are said to be linearly dependent if there exist constants c1,c2,c3,….cn not all zero such that: c1v1+c2v2+c3v3+……+cnvn=0 ————————-(i) Read More …
Numerical Methods for Engineers” (by Steven C. Chapra and Raymond P. Canale) is a widely used textbook that teaches computational techniques for solving problems in engineering and science. Here’s a summary of what the book covers: Modeling, computers, and error Read More …
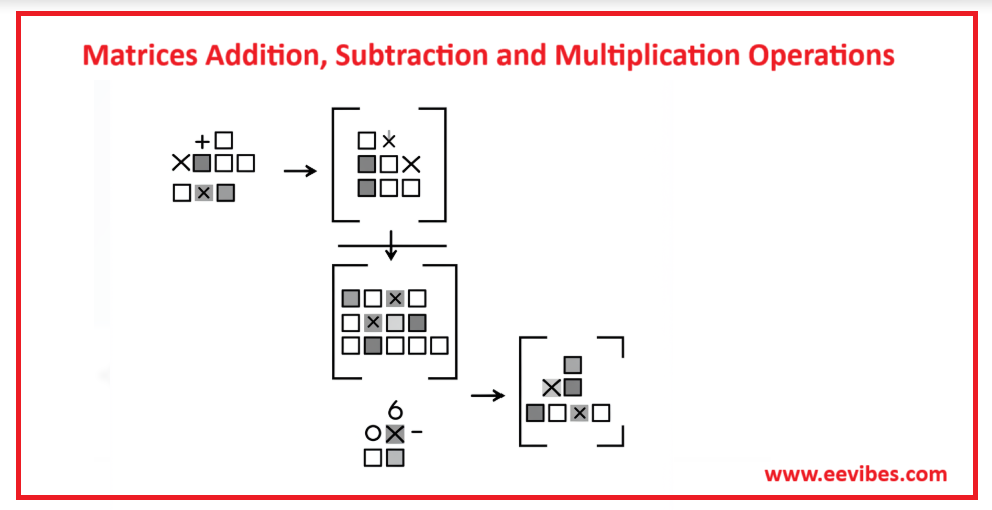
Introduction Power Method and Inverse Power Method for Eigen Values and Eigen Vectors. When looking for the greatest Eigen-pair, the power approach is usually used. The Inverse Power approach, on the other hand, is used to determine the smallest Eigen-pair. Read More …
Introduction In linear algebra, matrices are rectangular arrays of numbers, and operations like addition, subtraction, and multiplication follow specific rules. Below, I’ll explain each operation clearly and concisely, assuming you’re familiar with basic matrix notation. Matrix Addition Definition: Two matrices Read More …
Introduction to Principal Component Analysis In this article, you will learn about in depth about the Principal Component Analysis (PCA) technique which is used for reducing the dimension of data while preserving the variance. It is actually the transformation of Read More …
Introduction to eigen values and eigen vectors How to Find the Eigen Values and Eigen Vectors? explain with examples Eigen Values and Eigen Vectors has a great significance in many engineering problems specially in case of linear systems where we Read More …
Introduction to Matrix calculator This is an online tool that helps students for performing the arithmetic operations (addition, subtraction, and multiplication) online. It is simple and easy to use. You just need to select the order of matrices. In Matrix Read More …
Introduction to Secant Method What is the Secant method? Derivation of Secant method. The problem with the Newton Raphson’s method is that it requires the evaluation of the derivative for calculating each approximation of a root. Most of the times Read More …
Vector Space Definition in Linear Algebra what is the vector space in linear algebra? The collection of vectors (V1,V2,V3,…..) are said to form a vector space (V) if the following properties are satisfied For any two vectors u,v that belongs Read More …
Introduction to Linear system of equations How to solve system of linear equations in Linear Algebra? A linear equation in n variables x1,x2,x3,…..xn is an equation that can be written in the form of where b and coefficients are real Read More …