Introduction to Secant Method
What is the Secant method? Derivation of Secant method. The problem with the Newton Raphson’s method is that it requires the evaluation of the derivative for calculating each approximation of a root. Most of the times it is not that easy to calculate the derivative of a given function as the form of the function may be a complex expression. Also another ambiguity might be the derivative of the function at initial guess may be equal to zero. So considering both these constraints, there is another method which is called Secant Method.
There are two ways to derive the formula of Secant Method
- By substituting the definition of derivative in Newton Raphson’s Formula
- Using Graphical Approach
Derivation of Secant Method
Derivation using Newton Raphson method
As we know that the Newton Raphson method is given as

It can be noted that xi and xi+1 are two initial guesses. Since it is an open bracketing method so it is not necessary to bound the root of the original equation within the selected interval. The interval is updated using the most recent points. As will be shown in the example below.
Graphical Interpretation of Secant Method
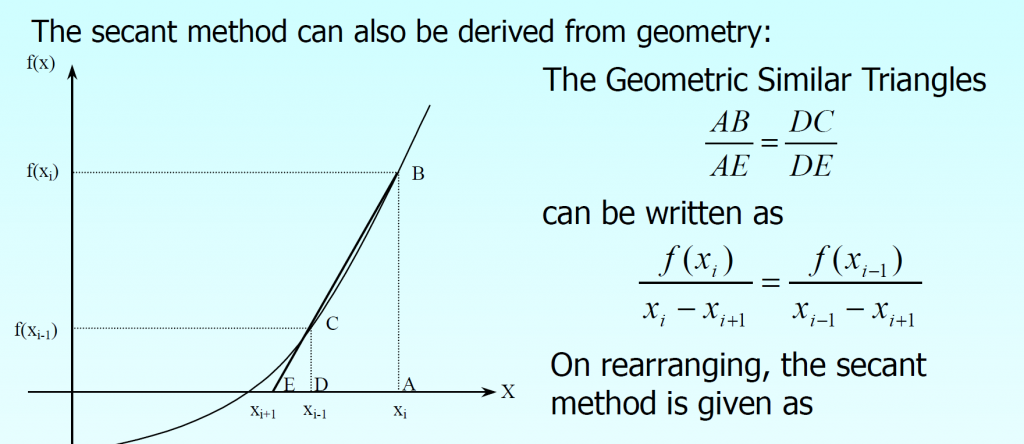
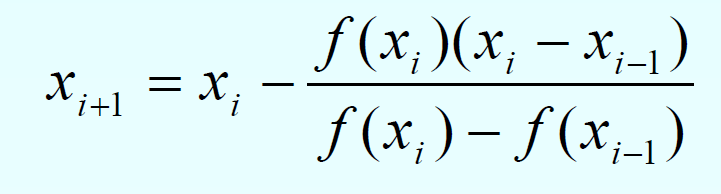
Advantages of Secant Method
- The first and foremost advantage of Secant method is that it converges very fast.
- We do not have to calculate the derivative of the function just like we need in Newton Raphson’s method.
- The interval is selected randomly. The condition f(a).f(b)<0 does not need to hold.
- The interval is updated using two recent values. Like x0 and x1, then x1 and x2 and so on.
Drawbacks of Secant Method
One of the drawbacks is when we start with two initial guesses at which function has same values. In this case the difference between two values of the function becomes zero. Hence the root is not updated.
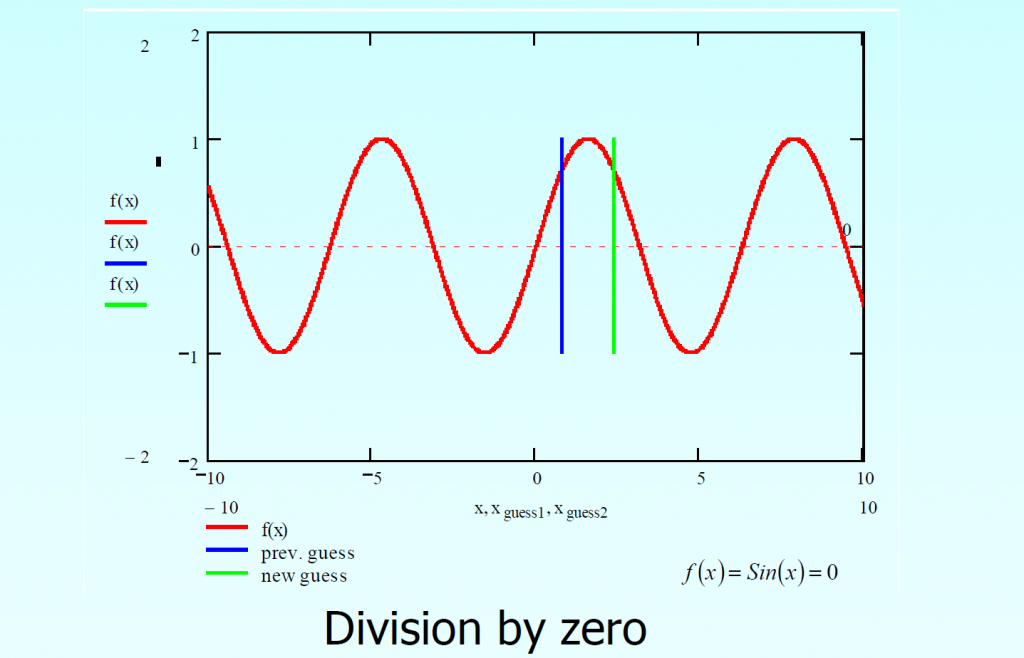
Second drawback is the jumping of root as shown below.
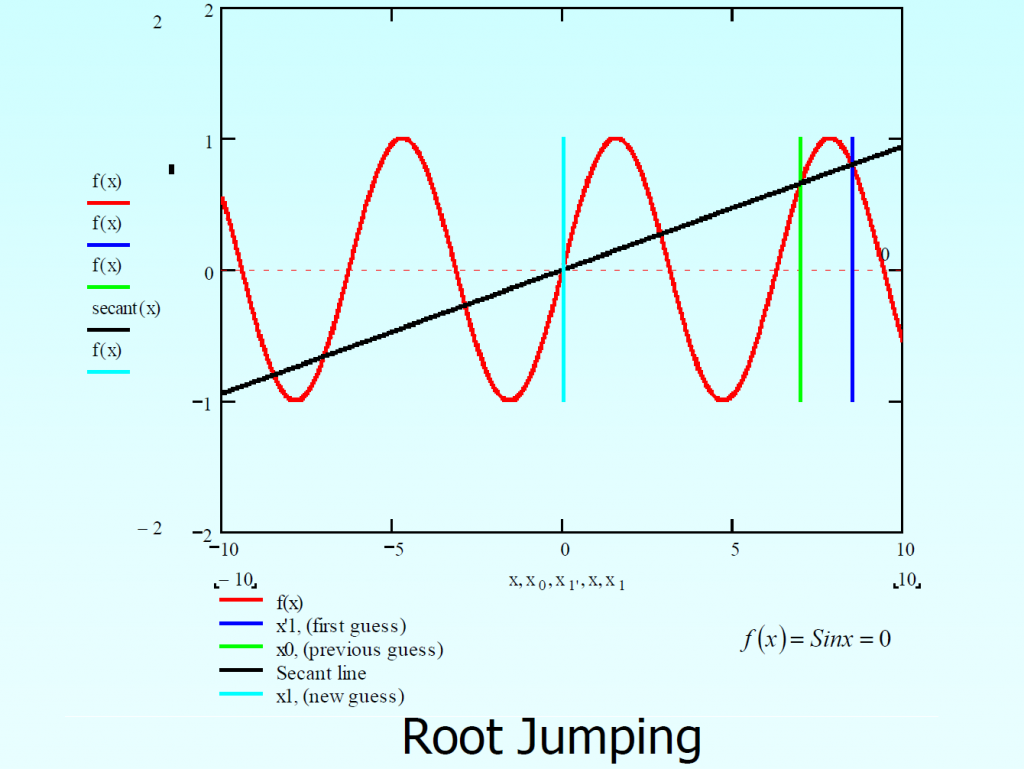
Algorithm for Secant method

Secant Method video lecture
https://www.youtube.com/watch?v=sEILMTuWZbk
Secant Method graphical derivation
https://www.youtube.com/watch?v=mX0stouUibI