Vector Space Definition in Linear Algebra
what is the vector space in linear algebra? The collection of vectors (V1,V2,V3,…..) are said to form a vector space (V) if the following properties are satisfied
- For any two vectors u,v that belongs to V, u+v should also belong to V.
Example
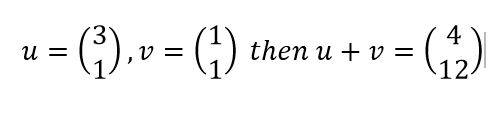
which means the resultant should also be present in the set of vectors V.
2. For any scalar a and v which belongs to V, a.v should also belong to V.
Example
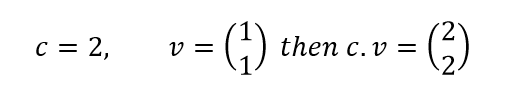
3. The third property is commutative property which is similar to the commutative property of real numbers. So, u+v=v+u.
4. For any three vectors u,v, and w, we always have u+(v+w)=(u+v)+w. This property associativity of additivity. This is also easy to interpret.
5. Zero vector must be the part of vector space (V). So, o+v=v and 0.v=0.
6. For any vector v, there exists a negative vector (-v) that satisfies v+(-v)=0.
7. c(u+v)=cu+cv for any scalar c and vectors u & v.
8. For two constants a and b it is always true ———> (a+b).v=av+bv
9. a(bu)=(ab).u for any two constants a and b and a vector u.
Generally speaking two properties are needed to be satisfied every time if we want to check the given set of vectors form a vector space or not.
- Addition
- Multiplication
If all the vectors of a given set satisfy these properties then they form space in V. The real numbers with zero vector form vector space.
what is the vector space in linear algebra?
Example of vector space
![]()
Example
For testing R^2 forms a vector space or not lets test both properties of vector space.
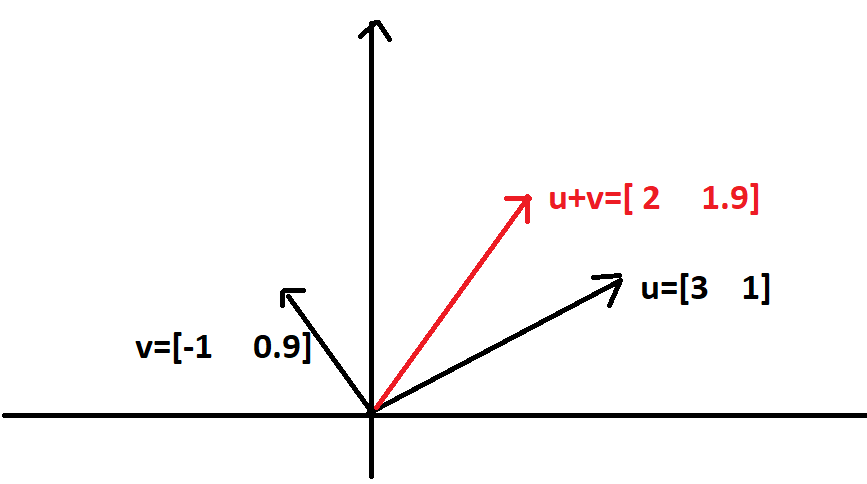
In this example it can be seen clearly that two vectors from R^2 gives the resultant of addition that is also representable in R^2. That is this is some vector that is presentable in first quadrant of R^2. That’s why u and v are closed under addition. Similarly if we multiply u with zero it becomes equal to zero. There is also a scalar 1 which results 1.u=u and so on. The same properties hold for higher dimensions R^n. For better understanding the concept of vector space, let us do another example.
Example
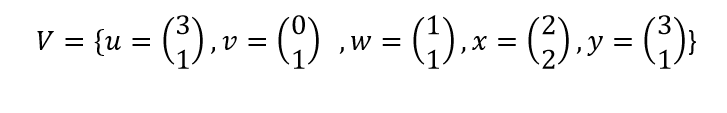
Now if we add any of the two vectors like x and v, then the resultant should lie within the set V.
so , x+v= [2 3]
so this set of vectors is not close under addition.
Vector Space Solved Example
NOTE: only one property is enough for making sure either the given set of vectors represent the vector space. We do not need to check multiplication property.
What is a Subspace in Linear Algebra?
Subspace is also some portion of a vector space V that is closed under addition and multiplication (just like vector space). If it does not satisfy both properties then it can not be a subspace of V.
Examples of Subspace in Linear Algebra
R^2 consists of four quadrants:
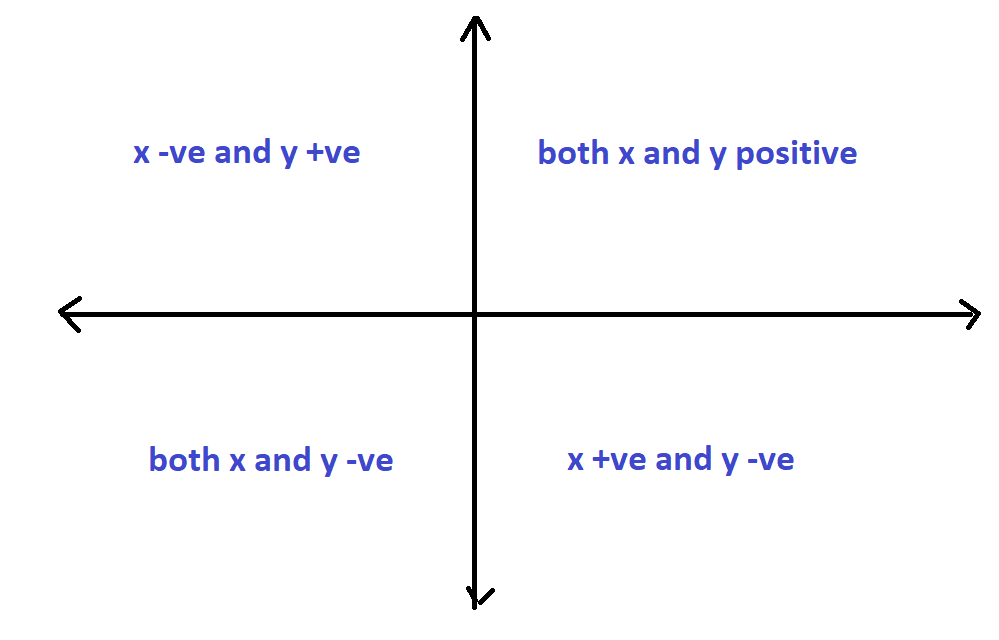
What are the possible subspaces of R2 ?
Explanation
- R2 is the subspace of itself.
- Any line passing through the origin is the subspace of R2
- zero vector is the subspace of every subspace.
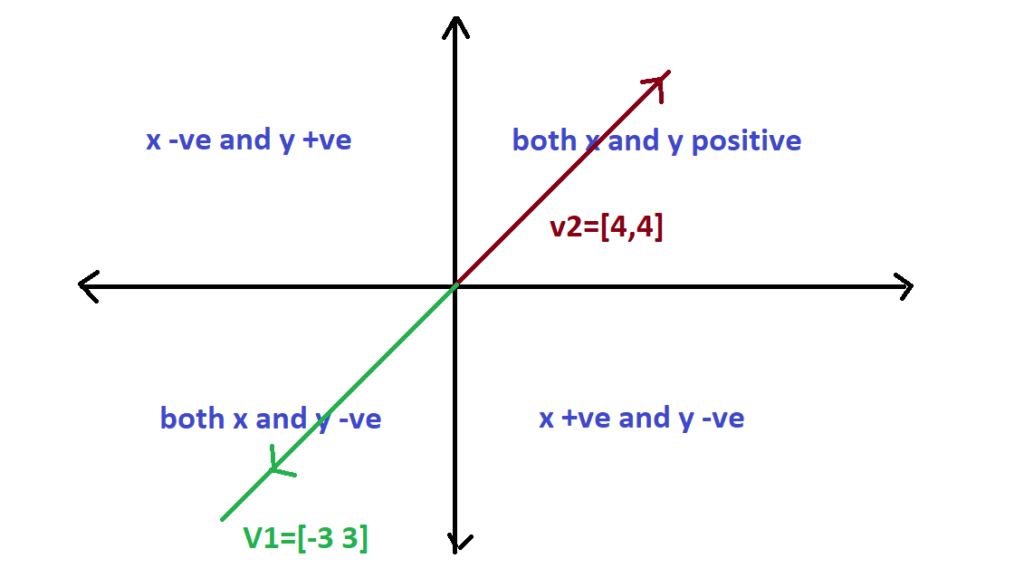
For understanding this we have selected two vectors v1= [-3 -3] and v2=[4 4]. Since the line must pass through the origin so 0.v1=0 and 0.v2=0. when these two vectors are added then resultant is =[1 1] that lies along this line. so line passing through the origin is close under addition. For multiplication, lets choose a constant k=3. So, k.v1=[-9 -9] that also lies along this straight line. Similarly any line passing through origin can be chosen as a subspace.
Is the first quadrant of R2 is the subspace of R2 ?
Answer: This is something very interesting for getting the more clear idea of vector spaces. As we know that in first quadrant, both x and y are positive. So, first additivity will be checked.
If we chose v1=[3 9]
v2=[1 10]
v1+v2=[4 19] that is representable in first quadrant. So, 1st quadrant is closed under addition. Now lets see either it is closed under multiplication or not?
If a positive constant is chosen then k.v1 will belong to first quadrant always. But if the constant is negative then the resultant will be shifted to the third quadrant.
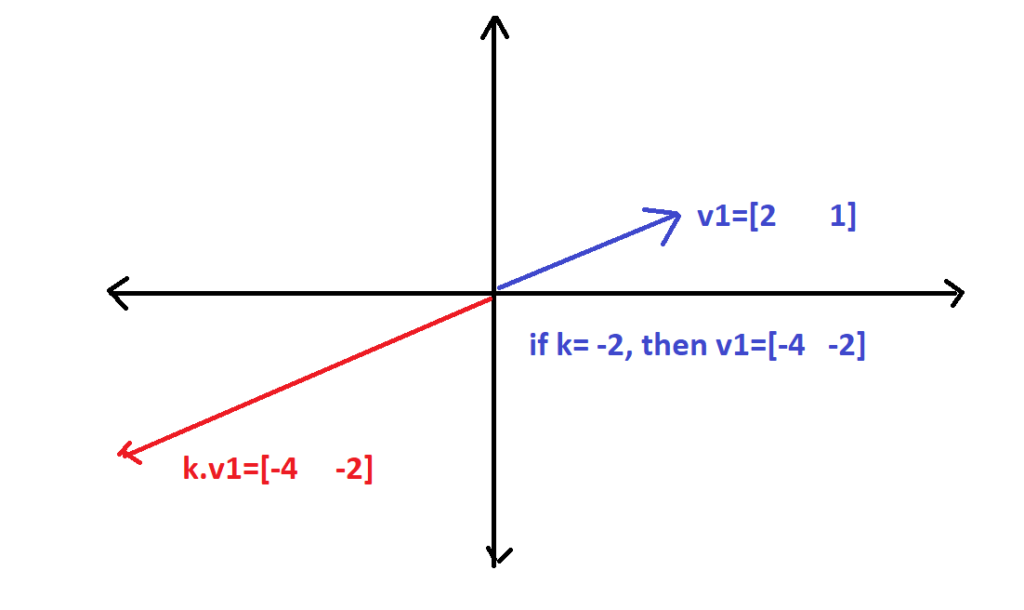
Since the resultant has moved out of 1st quadrant, so it is not the subspace of R2
Now, if we select third quadrant along with the 1st quadrant then lets see either they form the subspace of R2
or not?
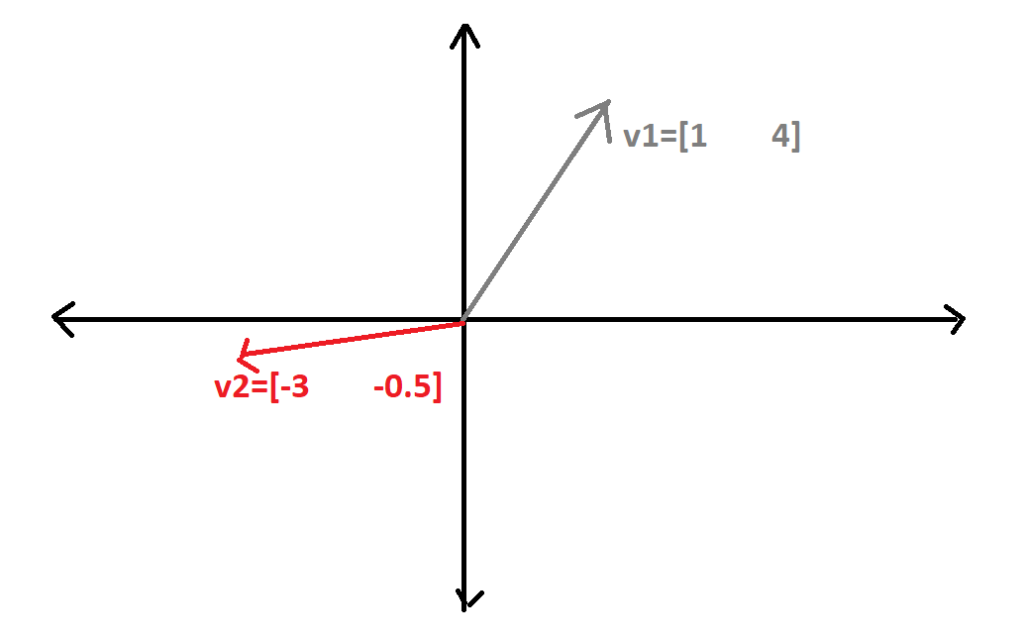
Here v1=[1 4], v2=[-3 -0.5] when we add v1+v2=[-2 3.5] that belongs to the 2nd quadrant. So the first and third quadrant do not form the subspace of R2
What are the possible subspaces of R3?
What are the possible subspaces of R3?
Also read here
what are the row spaces, column spaces and null spaces in Linear Algebra?

2 thoughts on “What are the Vector Space and Subspace in Linear Algebra ?”