Introduction to row spaces, columns spaces and null spaces
For any given matrix ‘A’ of order mxn, there are three types of spaces associated to them: row(A), col (A), and null (A). These spaces are linked with the solution of linear system of equations and have applications on larger scale.
Column space
The column space of a matrix Amxn is the subspace formed by the spanning of columns of A. The mathematical definition for this is
Col(A)={y ϵ Rm: y=Ax, for x ϵ Rn }
According to this definition, the column space of A is those vectors of A that can be expanded as Ax for some vectors x ϵ Rn . In such cases the column spaces is also referred as range of A or the image of A. The dimension of column space of A is determined by determining the linearly dependent column vectors of A which is also called the range of A. A system of linear equations Ax=b is consistent if b lies in the column space of A. When we say that b lies in the column space of A it means that b can be obtained by the linear combination of columns of A.
Row Space
For any matrix Amxn , the subspace of Rn spanned by the row vectors of A is called the row space of A.
Null space
Null space consists on all vector x for which Ax=0. It means we look for all values of vectors whose components will map our system coefficient matrix to origin (zer0).
Example
Lest find the basis for row space, column space and null space of the following matrix

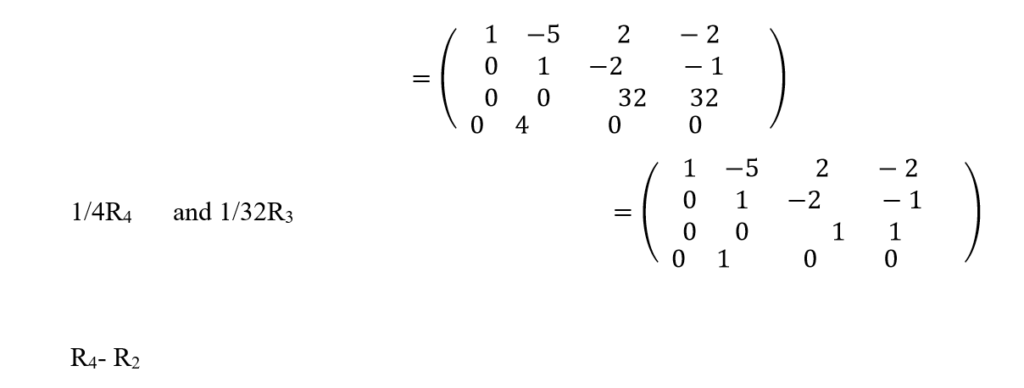

Dimensions of Row space and column space
Since there are four row/column vectors with leading 1’s. So, the dimension of row/column space is 4 in this above example. The same procedure can be followed for determining the null space of the above matrix. The only difference is that its augmented matrix will have form as shown given below
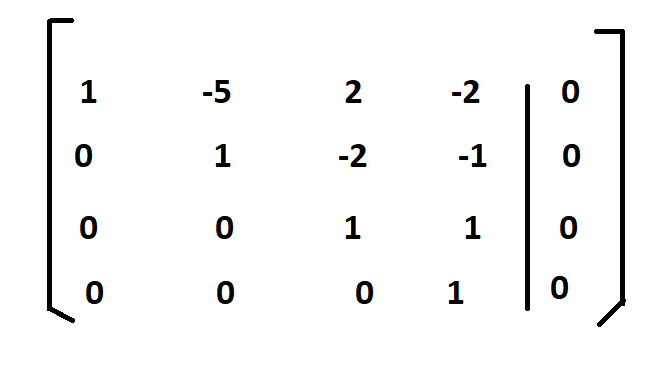
Now if the back substitution is performed we get
x4=0
x3+x4=0
——-> x3=0
x2-2×3-x4=0
——–> x2=0
x1-5×2+2×3-2×4=0
so all these variables are equal to zero. Hence null space of A consists of only zero vector. i.e., x=[0 0 0 0].
Examples of row space and column space
The following matrix is given in row-echelon form
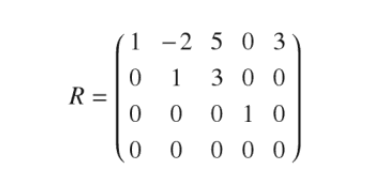

Find the basis for row space and column space

![]()

Properties of row spaces and column spaces
Suppose that the matrix A is obtained by the elementary row operations on some matrix B, then:
- The row space of matrix A is identical to row space of B.
- Any collection of column vectors of matrix A is linearly independent if the corresponding collection of column vectors of B is linearly independent.
A system of linear equations AX=B is consistent if and only if B lies in the column space of A. It means if b can be obtained or not as a linear combination of the column vectors of A.
Nullity:
Nullity can be characterized as the quantity of vectors present in the invalid space of a given network. All in all, the component of the invalid space of the grid An is known as the nullity of A. The quantity of straight relations among the ascribes is given by the size of the invalid space. The invalid space vectors B can be utilized to recognize these direct relationship.
Rank Nullity Theorem:
The position nullity hypothesis encourages us to relate the nullity of the information grid to the position and the quantity of characteristics in the information. The position nullity hypothesis is given by –
Nullity of A + Rank of A = Total number of columns of A matrix

Also read here
watch here for
How to find the row spaces and columns spaces of a matrix?
https://www.youtube.com/watch?v=3CMlUtlJ7xY
How to find the null space of a matrix?
https://www.youtube.com/watch?v=1ckjFQFwhSU
One thought on “what are the row spaces, column spaces and null spaces in Linear Algebra?”