
Introduction to Linear system of equations
How to solve system of linear equations in Linear Algebra? A linear equation in n variables x1,x2,x3,…..xn is an equation that can be written in the form of
![]()
where b and coefficients are real numbers and n is any positive integer. The equations
![]()
both are linear because they can be rearranged as:
![]()
Now test why the following equations are non-linear
![]()
System of Linear Equations
A system of linear equations is a collection of one or more linear equations that involve same variables in them like x1,x2,x3,…..xn. Generally a system of linear equations is defined as
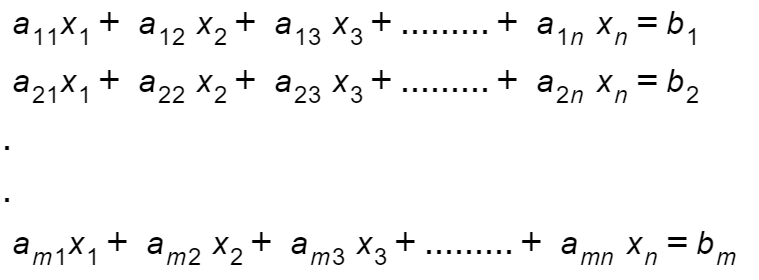
The above system is linear because each variable appearing in the equations in first power only. Now, Lets answer how to define and solve system of linear equations in Linear Algebra?
Homogeneous System:
If all bj=0, then the system is called a homogeneous system. If at least one bj is not equal to zero then the system is non-homogeneous. A homogeneous system has always a trivial solution (x1=0, x2=0,x3=0,…..xn=0). Since the zero vector always satisfies the linear equations in it. If a system is consistent then the solution set contains (a) a unique solution when there are no free variables or (b) infinitely many solutions when there is at least one free variable.
Classification of system
If m=n (well determined)
if m>n (over determined)
if m<n (under determined)
If at least one solution exists then the system is called consistent otherwise it is called inconsistent system. A system of linear equations has
- no solution or
- exactly one solution or
- Infinite many solutions
Whenever the system of coefficients of has the determinant equal to zero (a singular system) then it has either no solution or infinitely many solutions. If the determinant of a system is non-zero then the system has exactly one solution.
Properties of Determinant
We all know how to calculate determinant of a matrix of a 2X2 and 3X3 matrix. In order to calculate the determinant of higher order matrix we need to apply the Gauss Elimination for converting into upper triangular matrix. After Applying the row operations on it, the property of the determinant can be used which says ‘the determinant of a triangular matrix is the product of its diagonal entries’.
Other properties of determinant are as follows:
- A matrix is invertible only if its determinant is non-zero.
- For any two matrices A and B (of same order) det(A.B)= det(A).det(B).
- det(transpose(A)=det(A)
- If any two rows or column are same in a matrix, then determinant is equal to zero.
- The determinant is linear in each row.
- If any row or column of a matrix is equal to zero then determinant is also zero.
- Row operations do not change the value of determinant.
What is Rank in Linear Algebra?
The rank of a matrix is the number of leading ones in row-reduced echelon form rref(A) of a matrix. This form is obtained by applying the Gauss Elimination method. Consider the following example where I have assumed a matrix A and its rref form is shown as well. Since there are two leading 1’s in its rref form, so that’s why the rank of this matrix is 2.
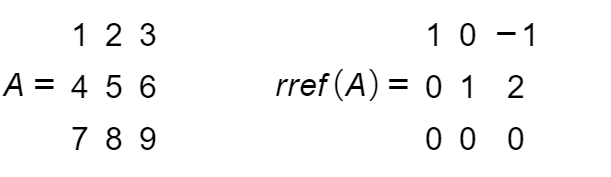
Consider a system of m linear equations in n variables, so the size of coefficient matrix is mxn. Then the following properties hold.
- If rank(A)=m, then the system is consistent.
- If rank(A)=n, then the system has at most one solution.
- If rank(A)<n then the system has either infinitely many solutions or none.
Gauss Elimination for solving system of linear equations
Write a Matrix as a Product of Elementary Matrices
In this video lecture I have explained how to express a matrix as a product of elementary matrices.
Solved example of a matrix as a product of elementary matrices
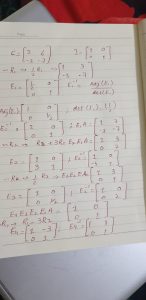
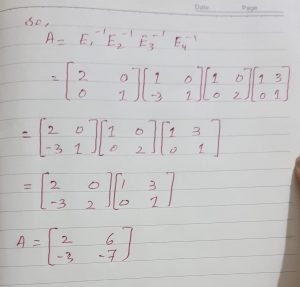
Also read here
https://eevibes.com/how-to-calculate-eigen-values-and-eigen-vectors/
2 thoughts on “Solution of Linear System of Equations using Gauss Elimination”