Introduction to eigen values and eigen vectors

How to Find the Eigen Values and Eigen Vectors? explain with examples Eigen Values and Eigen Vectors has a great significance in many engineering problems specially in case of linear systems where we want to study the “change”. In order to find the eigen values and eigen vectors a vector equation needs to be solved that is:

Ax=  λx.

where A is called the coefficient matrix of a linear system, x is the eigen vector corresponding to the value λ. One thing to be noted is that eigen values are always found of a square matrix. If the order of a matrix is n×n then at most ‘n’ distinct eigen values exist or at least one distinct eigen value can be found.  It can be seen clearly that x=0 is the solution of the above equation. But this solution does not give us the required information. So we are interested in some kind of non-zero eigen vectors so that we can interpret the obtained result.

Quiz for Eigen Values and Eigen Vectors

Before going into detailed discussion, let us see how much you know about eigen values and eigen vectors. Just try this quiz.

 

Spectrum and spectral radius:

The set of all eigen values of the system A is called the spectrum of A. While the maximum of absolute of eigen values is called the spectral radius of A. This concept will be shown in the later examples.

How to calculate eigen values and eigen vectors of a matrix?

For finding the eigen values and eigen vectors of a system the following steps are followed.

Ax=  λx

Ax -λx=0

(A- λI)x=0

det(A- λI)=0 gives a characteristic polynomial. The roots of this polynomial are called eigen values (they can be distinct or  repeated). Then the next step is to find eigen vectors corresponding to each eigen value. After finding the eigen values, the next step is to determine eigen vectors corresponding to them. This can be done by solving the equation (A- λI)x=0. For solving such system of equations, Gauss Elimination method can be used. So the answer is given How to calculate eigen values and eigen vectors of a matrix?

Algebraic Multiplicity

The order of an eigen value as a root of characteristics polynomial is called “algebraic multiplicity”. It mean how my many times an eigen value is repeated.

Geometric Multiplicity

It is defined as the number of linearly independent eigen vectors corresponding to λ. The difference between algebraic multiplicity and geometric multiplicity is called the defect of λ. The following figures depict the example which shows how eigen values and eigen vectors are determined. Also the defect has been calculated.

Here is the link of complete lecture

Application of eigen values and eigen vectors

Though eigen values have large applications in engineering and in many other fields. I have chosen a very interesting application that will elaborate more how their concept can be applied in real life.

Generally speaking eigen values tell about the amount of change and the eigen vectors show the direction of change or it can be said they depict in which the change is introduced.

Example:

An elastic membrane in x_1 x_2 plane with boundary circle x_1^2+x_2^2=1 is stretched so that a point p (x1,x2) goes over into the point Q(y1,y2) given by y1=5×1+3×2

y2=3×1+5×2

Find the principal directions, that is the direction of the position vector x of P for which the direction of the position vector y of Q is the same or exactly opposite. What shape does the boundary circle take under this deformation?

Solution:

 

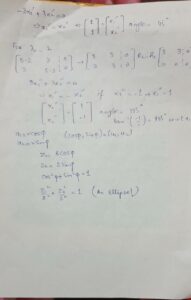
There are also some other applications of eigen values and eigen vectors. For example the growth of a particular community either increasing or decreasing can be decided by them. For this, all we need is to determine the eigen values of that community matrix. If eigen values are positive then their population is increasing otherwise its decreasing.

Similarly the NETFLIX uses singular values decomposition procedure of eigen values and eigen vectors for ranking the movies on its site.

How to check either the given vectors are the eigen vectors of a matrix?

https://www.youtube.com/watch?v=KQAQ76hv3dw&t=18s

How to calculate complex eigen values and eigen vectors of a matrix?

Power method for finding Eigen values and eigen vectors

The power method is an iterative method for finding the largest eigen value of a system. With little modifications, it can also be used for finding the intermediate and the smallest eigen values. The plus point of this method is that we obtain the corresponding eigen vector as well in this method.

Example of power method for finding largest eigen value

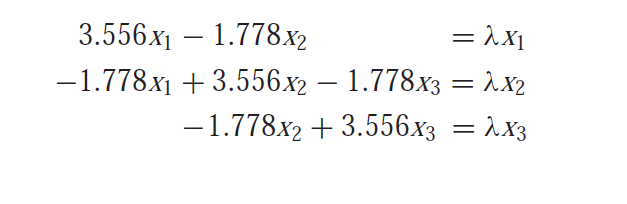
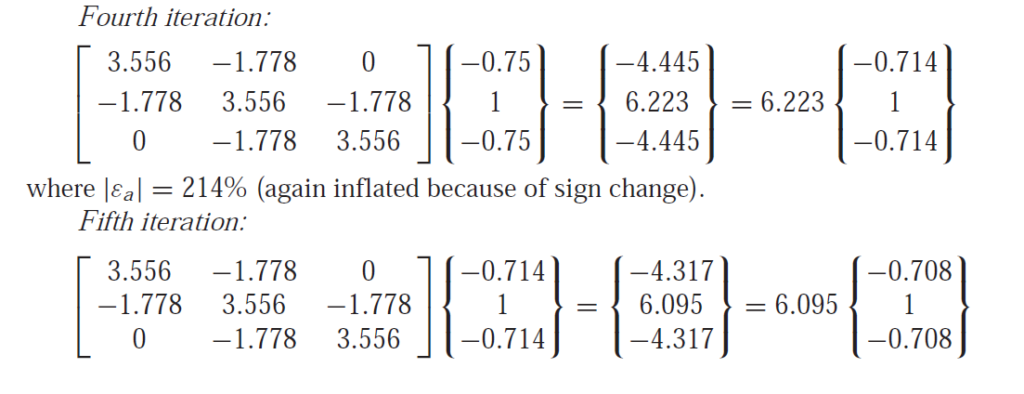
There are some cases where the power method will not converge to the largest value but to the second largest value.

How to determine the smallest eigen value using power method?

In order to determine the smallest eigen value of a system we just need to find the inverse of that system. Then we can apply the same power method as applied in the above example. This will determine the largest of 1/λ. Then  λ will be smallest eigen value. The following example illustrates this concept.

smallest eigenvalue power method example

Here 0.964 is the smallest eigen value of the above matrix A.

Watch here

Also read here

https://eevibes.com/mathematics/linear-algebra/what-are-the-linearly-dependent-and-independent-vectors/

How to test the given vectors are linearly independent or not?