
Table of Contents
Linearly Independent Vectors:
How to test the given vectors are linearly independent or not? The vectors v1,v2,v3,…vn in a vector space V are said to be linearly dependent if there exist constants c1,c2,c3,….cn not all zero such that:
c1v1+c2v2+c3v3+……+cnvn=0 ————————-(i)
otherwise v1,v2,v3,…..vn are called linearly independent, that is v1,v2,v3,….vn are linearly independent if whenever c1v1+c2v2+c3v3+……+cnvn=0 , we must have c1=c2=c3=0.
That is the linear combination of v1,v2,v3,….vn yields the zero vector.
How to determine either the vectors are linearly independent or not?
There are two ways to check either the vectors are linearly independent or not.
1-Graphically
2-Linear Combination Equation
Graphical Approach:
This approach is helpful for all those vectors that lie in 2D: means those vectors that have two components. Another point to consider is there should be nor more than three vectors for better understanding.
Lets consider an example:
V1=[1 2]
v2=[2 4]
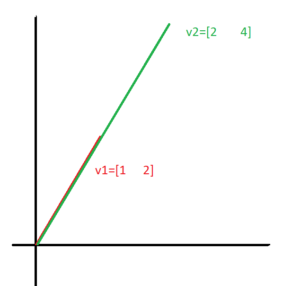
It can be seen clearly that V2 is obtained by multiplying v1 with 2 so v2=2.v1. So v2 is linearly dependent on v1.
now lets consider another example
v1=[1 3]
v2=[2 3]
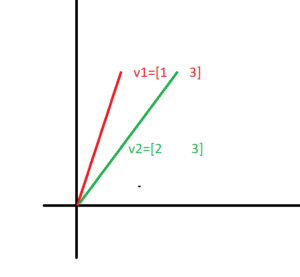
As it can be seen clearly that v1 does not depend on v2 nor does v2 depend on v1 because there is no constant whose multiple of v1 gives v2. In this case v1 is linearly independent of v2. Hence the linearity equation does not satisfy.
Mathematical Description
Now lets sole these two equations mathematically for verifying the graphical concept of linearly dependent and independent vectors.


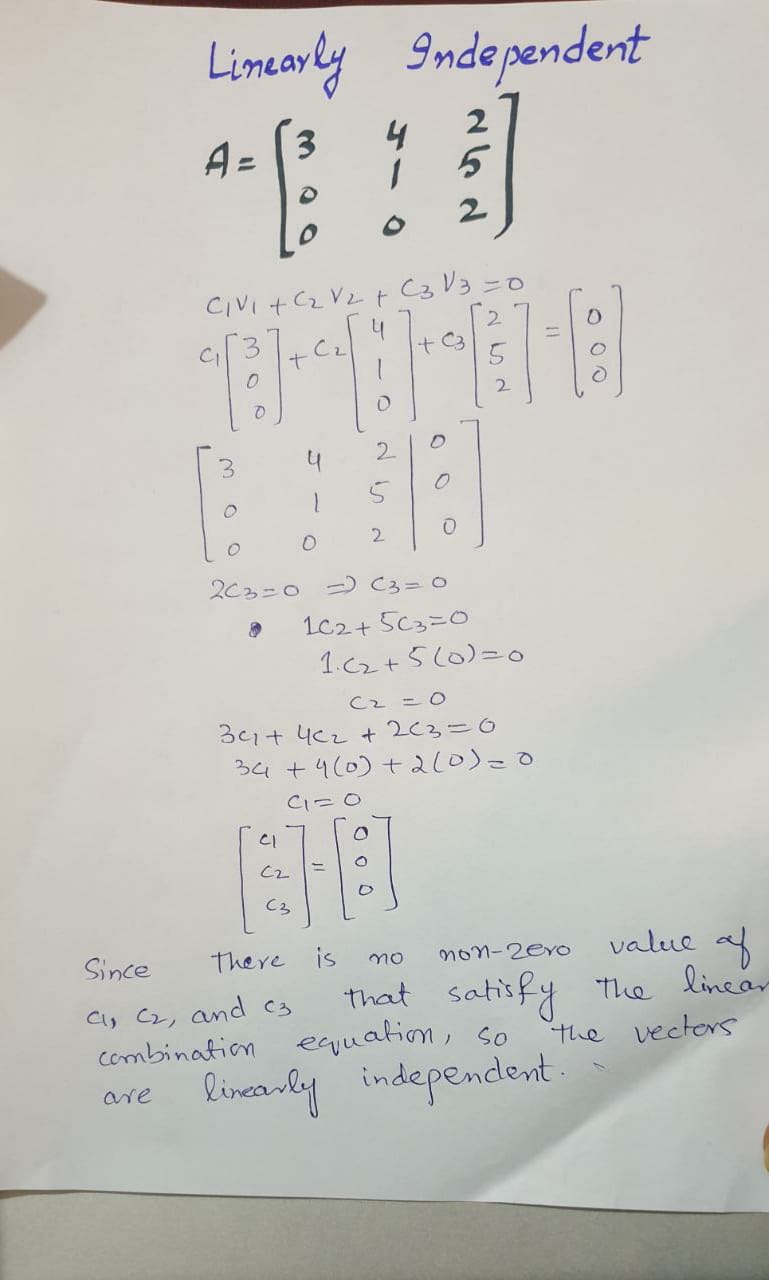
How to find the given set of vectors are linearly independent or not?
https://www.youtube.com/watch?v=wHVRwUl08Bk&t=469s
Example of finding linearly independent vectors
https://www.youtube.com/watch?v=vmsROZUgsEc&t=7s
For what value of h the vectors will be linearly dependent?
https://www.youtube.com/watch?v=1jAMJeeEHcw
watch here for more details
https://www.youtube.com/watch?v=PtRF6ZCqHWg
Also read here
https://eevibes.com/how-to-calculate-eigen-values-and-eigen-vectors/
3 thoughts on “How to test that the Given Vectors are Linearly Independent or Dependent?”