Introduction to span of a vector space

For the given set of vectors v1,v2,v3,……vn that belong to a vector space V and non-zero constants c1,c2,c3,….cn if they can generate another vector x(x1,x2) using the relation

c1v1+c2v2+c3v3+…….+cnvn=x

then we will say these vectors span in the vector space R2.

By spanning we mean that is it possible to generate another vector from the given set of vectors or not. If it is possible then the given vectors span in that vector space.

It has been observed that if the given vectors are linearly independent, then they span the vector space V.

Lets say hat we have a set of vectors u1,u2,u3,….un. Then it can be observed that every vector is a linear combination of itself and the remaining vectors as shown below.

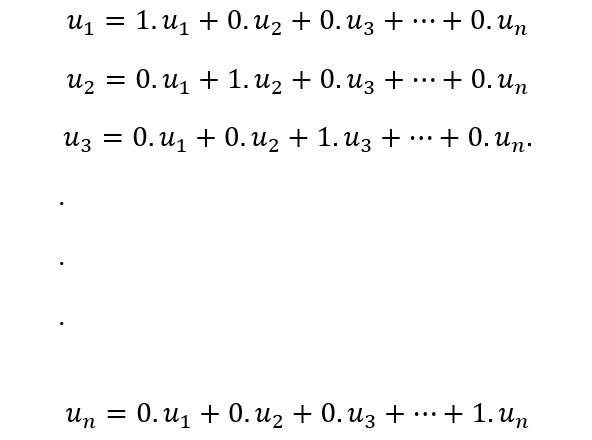
For more detail watch here 

span of u1=(2,4) is a line through the origin.

span of (u1,u2) is a plane through the origin keeping in mind that u1 is not the scalar multiple of u2.

Read here for more

https://eevibes.com/mathematics/linear-algebra/what-are-the-vector-spaces/