Table of Contents

Diagonalization of a matrix

How to diagonalize a matrix? Example of diagonalization. An nxn matrix A is said to be diagonalizable if there exists an invertible matrix P such that A=PDP^–.

Procedure for diagonalizing a matrix

For diagonalizing a matrix A, the first step is to find the eigen values of it. Then find the corresponding eigen vectors of it. All the eigen vectors should be linearly independent if you want to diagonalize a matrix A. Otherwise, A is not diagonalizable. If you get the distinct eigen values then by the theorem eigen vectors corresponding to distinct eigen values are linearly independent. But if the eigen values are repeated, then the corresponding eigen vectors can be or cant be linearly independent. The diagonal matrix we obtain after the process contains the eigen values in the main diagonal.

This is also called the method of eigen values. Since eigen vectors can be represented as a scalar multiple that’s why the diagonalization of matrices is not unique.

Example of diagonalizing a matrix.

The first example shows how we got repeated eigen value, but since the corresponding eigen vectors are linearly independent so A is diagonalizable. But in the second case again with the repeated eigen values, there were only existing two eigen vectors so that is why those vectors were linearly dependent. Hence that matrix was not diagonalizable.

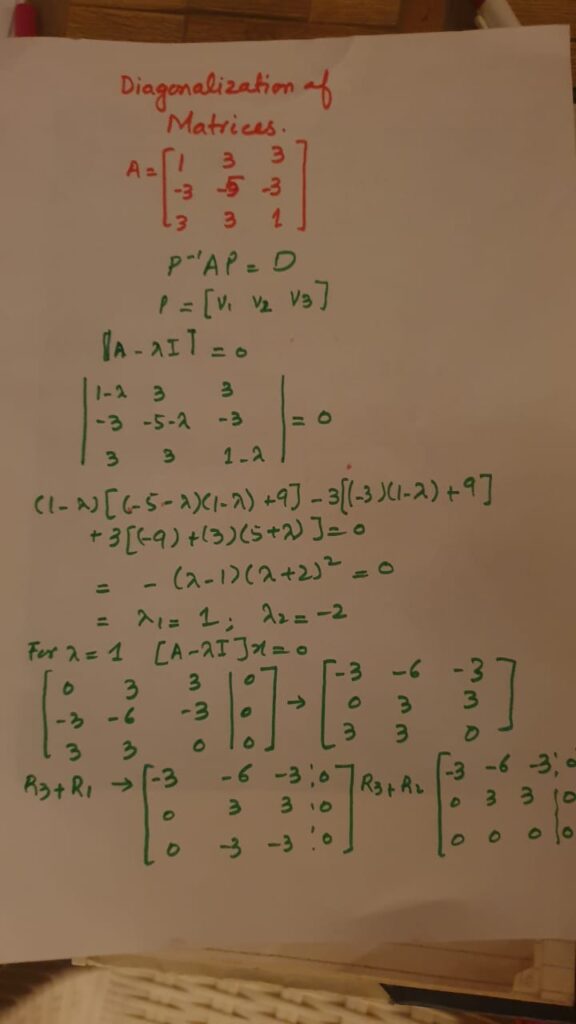
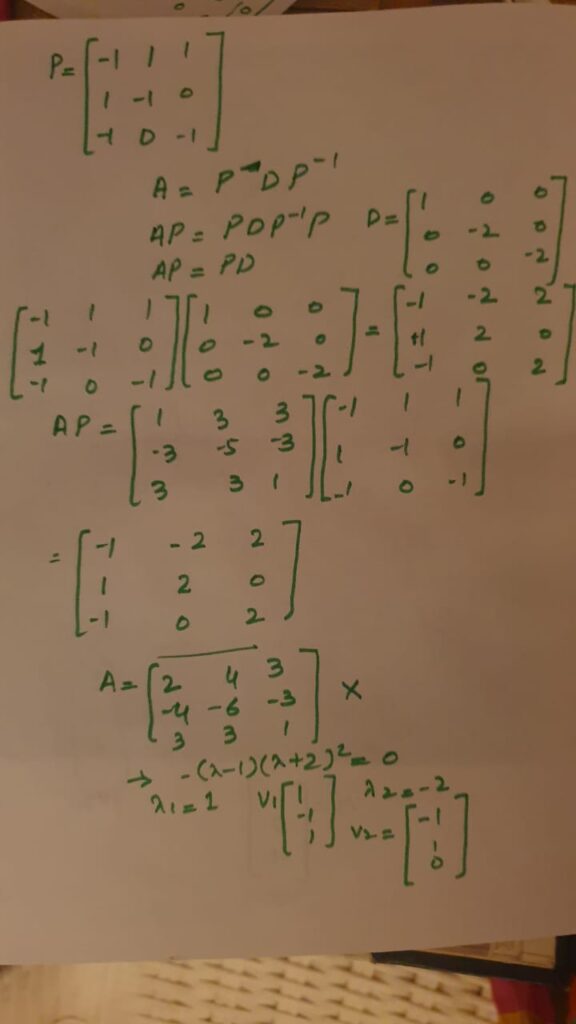
Video lecture for diagonalization of matrices-example

https://www.youtube.com/watch?v=ytF-gjmMG_k&t=6s

watch here

Diagonalization example for repeated eigen values

In case of the repeated eigen values, the diagonalization may be or may not be possible. It all depends on the dimension of the eigen space. If there is a defect present in the matrix, then diagonalization is not possible. Or in other words if there is the possibility of existing of linearly independent eigen vectors for the repeated eigen values, then it is diagonalizable.

Example of diagonalization of a matrix

Application of diagonalization

One of the applications of the diagonalization is to find the higher powers of a matrix. So, Lets assume that if we want to calculate

A², A³,……A^Kthen it can be done using the concept of diagonalization.

For example,

A²=(A)(A)=(PDP^-1) (PDP^-1)

=PD(P^-1 P)DP^-1

=PD²P^-1

Similarly,

A³=( A²)(A)=( PD² P^-1) (PDP^-1)

= PD²(P^-1 P)DP^-1

= PD³P^-1

A^k= PD^kP^-1

https://www.youtube.com/watch?v=ci4cZTBCnIs&t=4s