Why do we use linear algebra?
What are the matrices and their types ? Linear Algebra is the branch of mathematics in which we study about the all the physical systems that can be modeled as linear systems. Linear algebra deals with solving the linear system of equations that are developed from some chemical reactions or road map or from component manufacturing company. The word “algebra” is derived from the word “aljabar” meaning broken parts.
What are the matrices?
The matrices are the key unit or building of linear algebra. The general expression for matrix is
A=[aij ]m×n
where ‘a’ represent the entry of the matrix and ‘i&j’ are the subscript which shows the corresponding row and column of the matrix. A matrix can have any number of rows and columns which determine the order of the matrix. Here there are m number of rows and n number of columns and mXn define the order of the matrix.
What are the vectors?
Vectors are the special case of matrix. If there are m number of rows and a single column, then we say it as “column vector” . If there is only one one row and n number of columns then it is called “row vector”.
The following example illustrates the example of row vector and column vector.
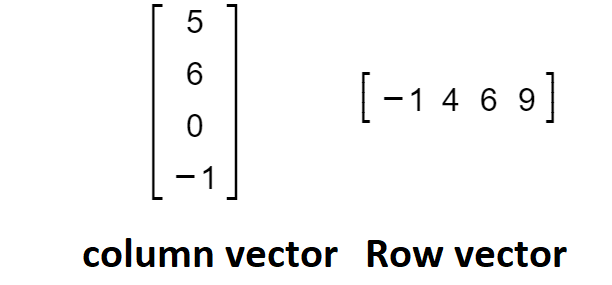
Types of matrices
There are various matrices and each of them has its specific characteristics. They are described below with an example.
Square matrix
If a matrix has equal number of rows and columns or if m=n, then such matrices are called the square matrices
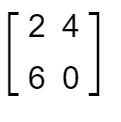
Rectangular matrix
If number of rows and columns of a matrix are not equal then such matrices are called rectangular matrices.

Symmetric matrix
if AT=A then such type of a matrix is called a symmetric matrix. The following example shows a symmetric matrix

Skew Symmetric matrix
If transpose of A is equal to negative of A i.e., AT=-A then such matrix is called skew symmetric matrix.
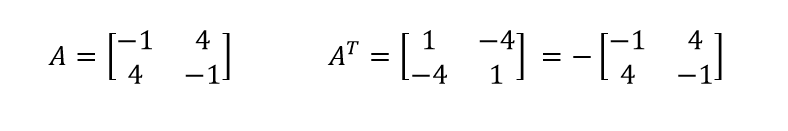
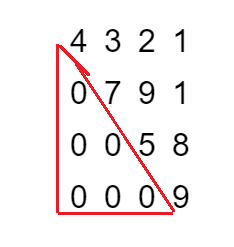
Upper triangular matrix
If a matrix has non zero entries above and on the main diagonal, then it is called an upper triangular matrix.
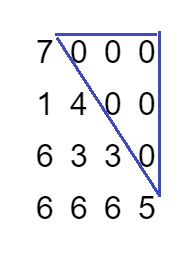
Lower triangular matrix
If all the entries of a matrix below and on the main diagonal are non zero, then we have a lower triangular matrix.
Diagonal matrix
If a matrix has only non-zero entries on the main diagonal then it will be called a diagonal matrix.
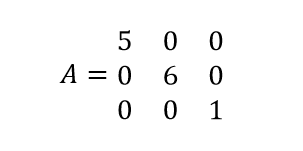
In linear algebra we might encounter with any of these matrices.
Scalar matrices
These are the diagonal matrices whose values are identical to each other. Consider the following matrix:
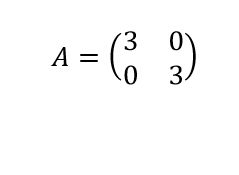
In this matrix, the scalar is 3.
The scalar matrices satisfy the following property
If S is any scalar matrix with scalar value= 2 and A is any other matrix then
AS=SA=cA.
For this consider the following example
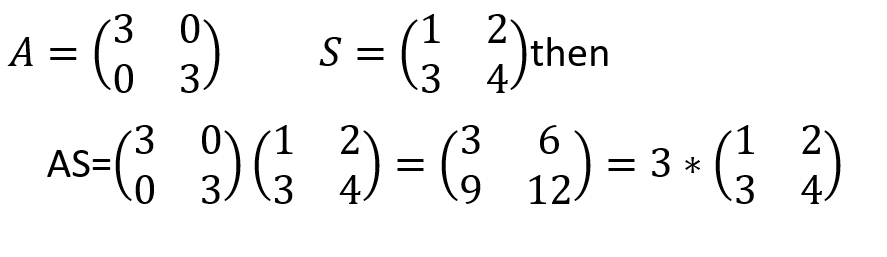
Also read here:
https://eevibes.com/how-to-define-and-solve-system-of-linear-equations-in-linear-algebra/
One thought on “What are the matrices and their types ?”