Introduction Finding extreme values of a function involves identifying the maximum and minimum values the function can achieve. These values can occur at critical points (where the derivative is zero or undefined) or at the boundaries of the domain. Steps Read More …
Category: Mathematics
How to find the basis of a vector space V?
How to find the basis of a vector space? How to find the basis of a vector space V? In order to find the basis of a vector space , we need to check two properties: The vectors should be Read More …
Complete List of Linear Algebra Video Lectures 2024

Here is the Complete List of Linear Algebra Course: Lesson 1: Matrix Basic Operation Lesson 2: Properties of determinant with example https://www.youtube.com/watch?v=Xl1FV6EVIQE&list=PLacdleb4rX6-ROG5FT-ijn74jRtrszIU4&index=40&pp=gAQBiAQB Lesson 3: Nodal Incident matrices for networks Lesson 4: Solving system of linear equations using Gauss Elimination https://www.youtube.com/watch?v=Q_NHw_RZsZs&list=PLacdleb4rX6-ROG5FT-ijn74jRtrszIU4&index=7&pp=gAQBiAQB Read More …
What is the Gram Schmidt Procedure? Explanation and Example
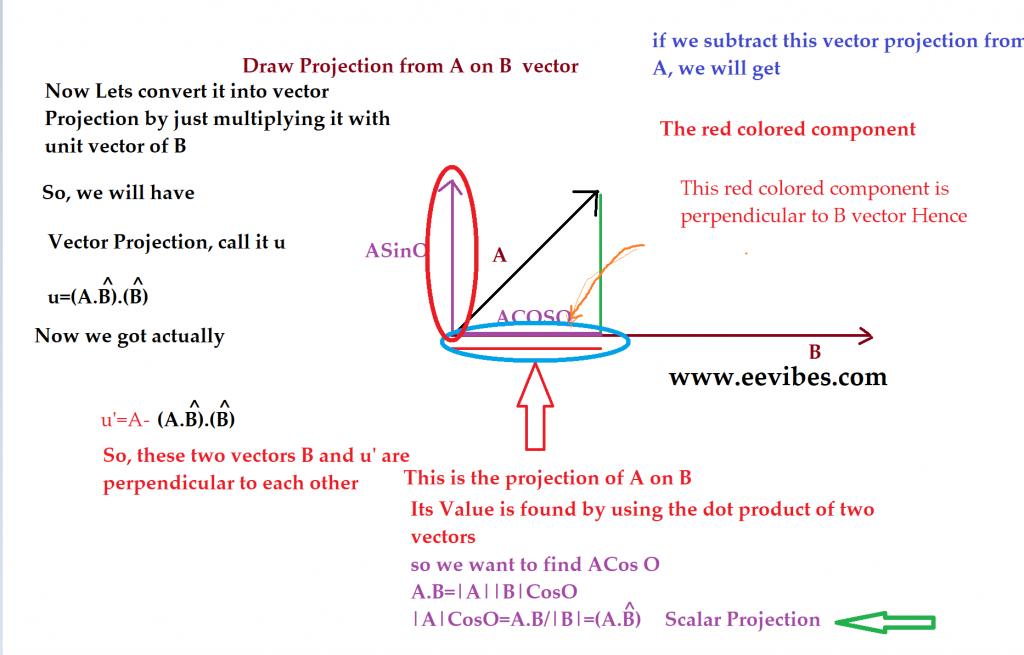
Since, by applying head to tail rule on the vectors components, we can generate the original vector A. After that we need to find the projections of one vector to another vector. This projection is subtracted from the other vector and hence these two vectors become orthogonal.
So, for two vectors A and B lets say we want to generate a new set of vectors W and Y that will be orthogonal to each other. We will assume
What are the Properties of Determinant?
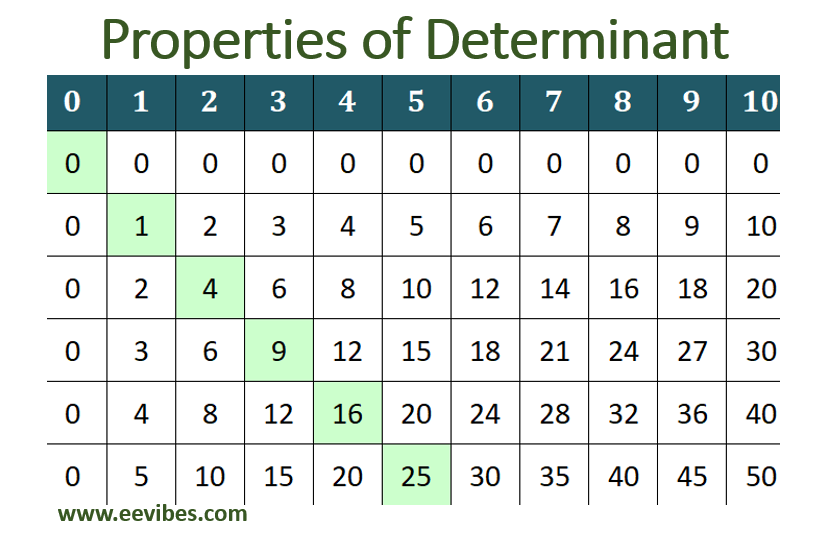
Properties of Determinant In this article, I have discussed some of the properties of determinant. Determinants are mathematical objects that are associated with square matrices. They have several properties that make them useful in various mathematical applications. Here are some Read More …
How to test that the Given Vectors are Linearly Independent or Dependent?

Linearly Independent Vectors: How to test the given vectors are linearly independent or not? The vectors v1,v2,v3,…vn in a vector space V are said to be linearly dependent if there exist constants c1,c2,c3,….cn not all zero such that: c1v1+c2v2+c3v3+……+cnvn=0 ————————-(i) Read More …
What is Linear combinations, Linear dependence and Linear Independence?
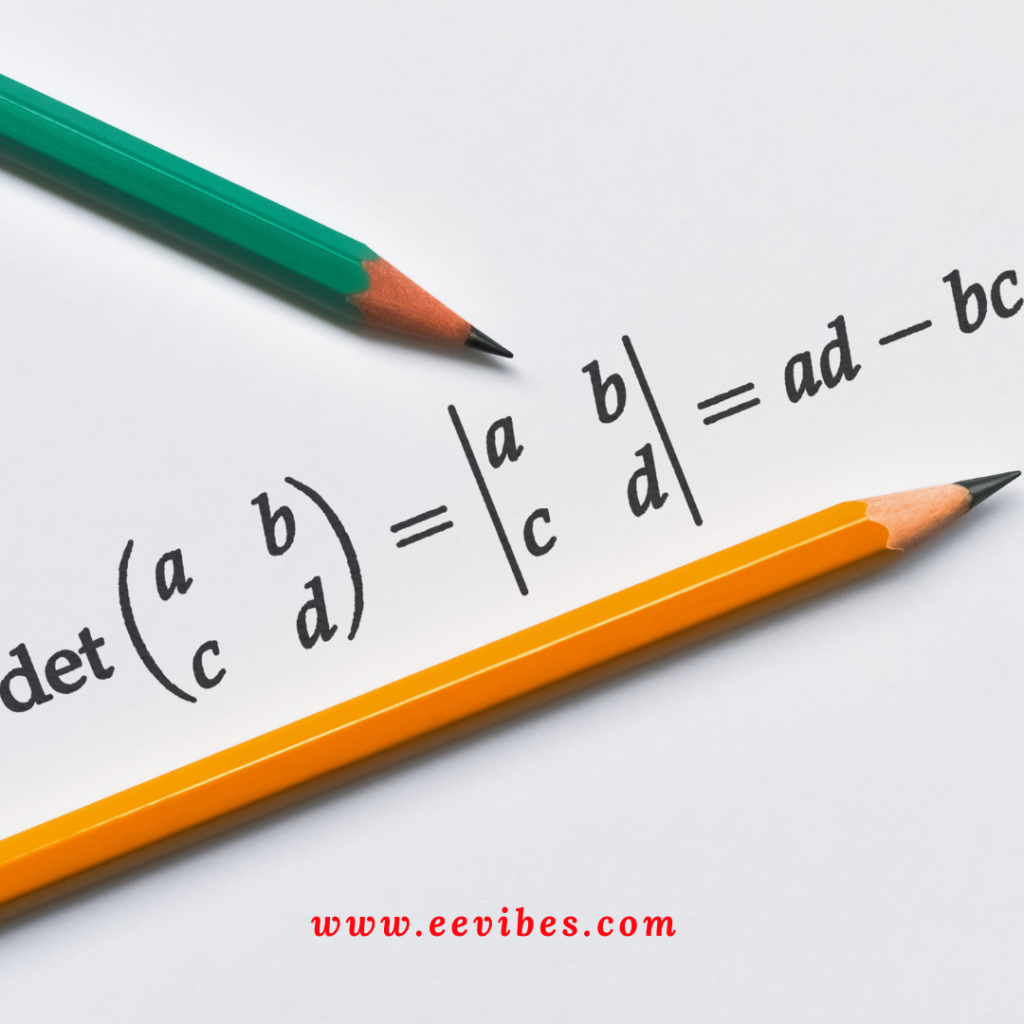
In this article you will get the idea of What is Linear combinations, Linear dependence and Linear Independence? Linear algebra is important for the turn of the mathematical branch. It is one of the main branches of math that can Read More …
Representation of Floats in Single Precision

Representation of floats in computer system In this article I have discussed about how to represent floats in computer system? Real numbers are stored as floats in computer system. The more bit size will provide us larger range of numbers Read More …
Integral calculus: Definition, formulas, types, and examples
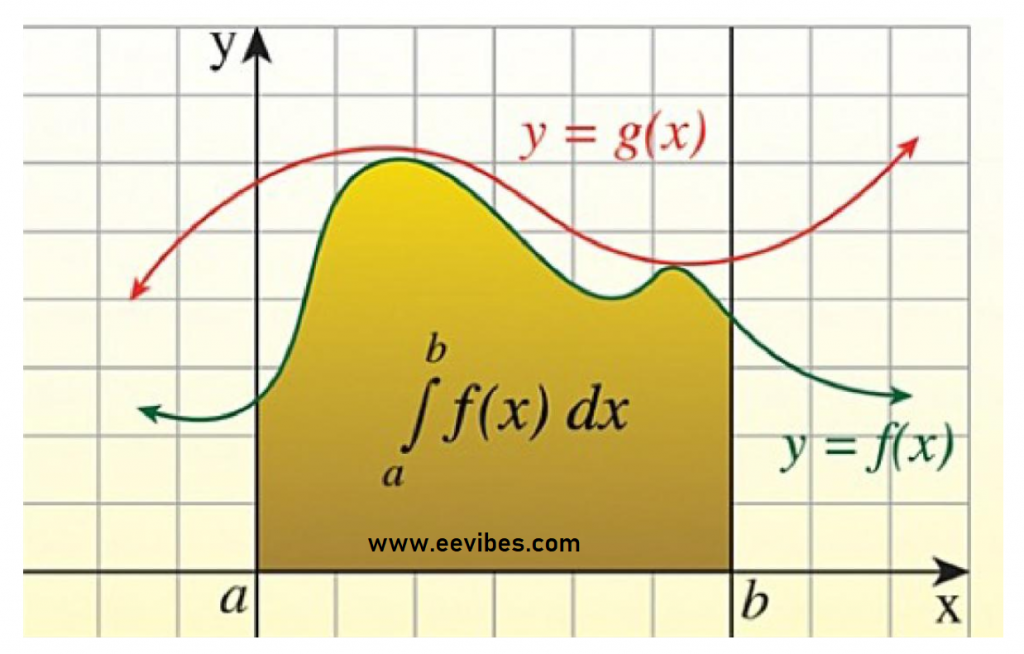
Introduction In calculus, integrals are used to find the volume and area of the region. This branch of calculus also provides graphs of the integral functions. Integral is used to solve the complex problems of calculus with respect to integrating Read More …
What are the shortcuts for finding the determinant of a matrix?
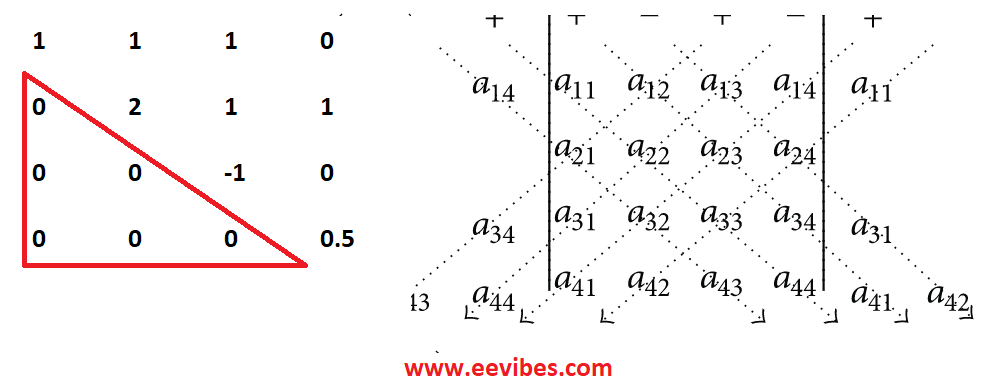
Introduction In this article, I will discuss the shortcuts for finding the determinant of a matrix. Determinant has great significance in linear algebra. There are many practical problems that can be modeled as a linear system. When the systems are Read More …