
Representation of floats in computer system
In this article I have discussed about how to represent floats in computer system? Real numbers are stored as floats in computer system. The more bit size will provide us larger range of numbers to be represented. We have two approaches for storing floats that are:
- single precision method
- double precision method
What is the single precision?
In single precision, we have reserved 32 bits for representing a single number. The distribution of 32 bits is as follows:

The 31-bit is reserved for representing the sign of the number. If we are representing a positive number then sign bit stores ‘0’ and if the negative number is being stored, then sign bit=1.
Here exponent has 8-bits. The exponent is always stored as a biased component. By biasing we mean that it is always stored by adding a constant ‘127’ in it. The purpose of biasing is to store the more small number in single precision. Since the more smaller number will have negative value of exponent. The value of the biased component is determined from the range of 8-bits signed numbers. (-128 to 127).
23-bits has been reserved for storing the mantissa: the fractional part of the number. There is a hidden bit ‘1’ that needs to be amended every time you read the stored number. The hidden ‘1’ indicates that the number is actually normalized.
What are the IEEE standards for single precision?
According to IEEE standards, some of the bit patterns have been reserved for representing the specific numbers. These are shown below
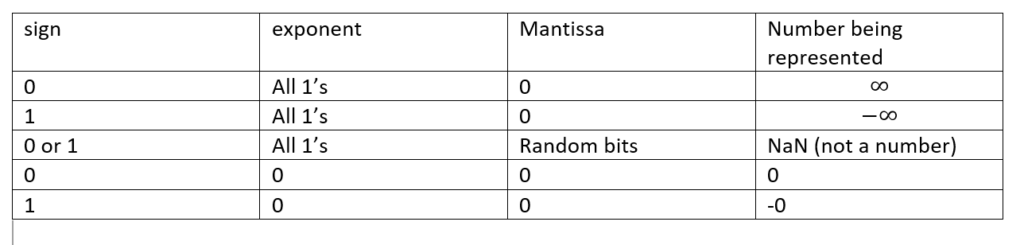
From here we conclude that two combinations of exponent i.e., 1111 1111 and 0000 0000 can not be used for storing the numbers as they are used for representing the special numbers (infinity and zero). The rest of the combinations that are available are from (1111 1110 and 0000 0001).
How to store a decimal number in single precision?
In order to store a decimal number 10.5 in single precision, follow these steps.
- First find the binary equivalent of the number which is 1010.10 in this case.
- Convert that binary equivalent into the scientific notation of binary representation: 1.01010 X 23
- From here you will get exponent=3.
- Add 127 into exponent (3+127=130)
- Find binary equivalent of 124 which is 1000 0010
- Store it in place of exponent
- Also drop 1 from mantissa and you will have remaining part that is 0101000000000…..
- Always start storing mantissa from left hand side i.e., from bit number 23. Since point is placed there.
- Since it is a positive number, that is why sign bit=0.
- The number is stored as follows

How to read a stored number in single precision?
In order to read which number is stored in the bit pattern follow these steps:
- First note down the sign bit, if it is zero, then the number is positive otherwise it is a negative number.
- read 8 bits of exponents, find its decimal equivalent. Whatever that decimal equivalent is subtract 127 from it.
- Then read bits from mantissa and place 1 before it.
- Lets do an example of reading a stored number.

sign=0 so its a positive number
exponent= 1000 0010 = 130
subtract 127 from it i.e., 130-127=3
mantissa=1.01010
So it can be written as
1.01010 X 23
convert it into decimal form
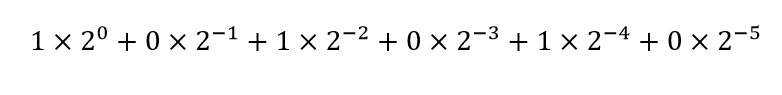
where 23 is equal to 8
so this becomes 1.3125*8=10.5 which was the actual number we stored.
Also watch here
https://www.youtube.com/watch?v=0SNjrlBC1C4
How to represent the largest and smallest positive number in single precision?
https://www.youtube.com/watch?v=WCxb8mxiSTw
What is the machine epsilon in single precision?
https://www.youtube.com/watch?v=DU2ZenZSLfs
Also read here
https://eevibes.com/computing/introduction-to-computing/what-are-number-systems/
What are the Different Types of Number Systems in Computing?