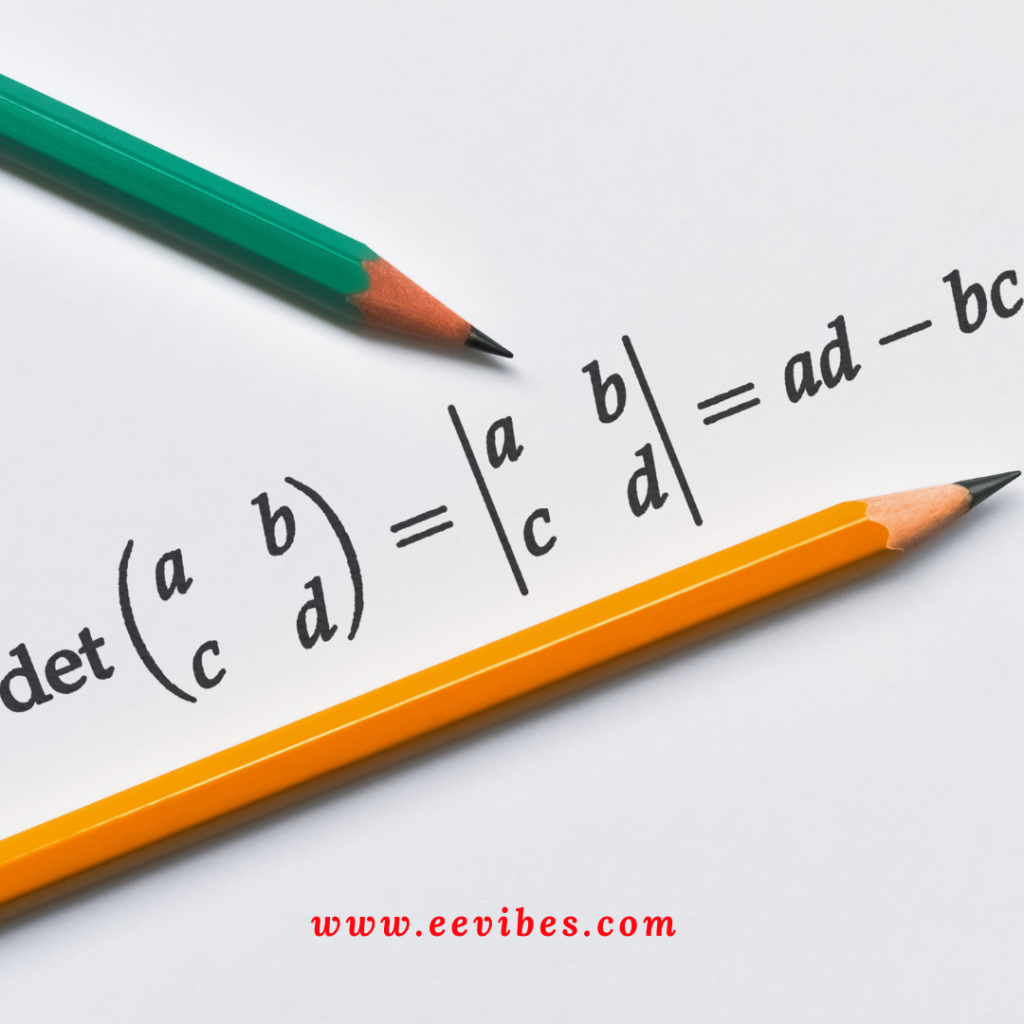
In this article you will get the idea of What is Linear combinations, Linear dependence and Linear Independence? Linear algebra is important for the turn of the mathematical branch. It is one of the main branches of math that can likewise allude to the mathematical designs contained under extra working and consolidates the augmentation of scalar numbers with the hypothesis of exact frameworks matric choices vector and linear spaces. Changes .The line algebra manages mathematical vectors and networks and particularly vector spaces and line transformations. Not at all like other mathematical regions, which are frequently comprised of new ideas. fields of material science to current algebra and its advantages to engineering and medical fields.

Table of Contents

Introduction

Linear algebra is quite possibly the most notable mathematical discipline because of its rich background and numerous helpful resources in the field of science and innovation .Solving line mathematical framework and computer-counting antonyms are two instances of issues we will make. handling the line algebra we have gained the most from this review .The Dutch mathematician got arrangement recipes in 1693 and in 1750 another mathematician presented a strategy for tackling different mathematical frameworks. This was the initial phase in the improvement of linear algebra and network hypothesis. of the appearance of computers the network strategy got a great deal of consideration .John von Neumann and Alan Turing were famous trailblazers in computer science and accomplished some work in the field of linear algebra too. Line .Current computer line algebra is extremely famous this is on the grounds that the field is presently perceived as a vital device in numerous computer branches .For instance, computer illustrations, robots and j model geometry and so on .

https://youtu.be/3-4KqqYB9KA

Linear Combinations

For the most part, statistics state that a composite component is a compound product (Poole, 2010). In this sense, for example, a combination of lines is the functions f (x), g (x) and h (x).

\begin{equation}
2 f(x)+3 g(x)-4 h(x)
\end{equation}

Definition of Linear combinations

If we have a set of vectors {v₁, v2, v3…v_n} in a space of vector v, any vector of the form

\begin{equation}
V=a_{1} v_{1}+a_{2} v_{2}+a_{3} v_{3}+\cdots a_{k} v_{k}
\end{equation}

For some scalars a1, a2——a_k is called a combination of linear v1, v2—v_k

https://youtu.be/tF-WSYCZjSA

Basic Vector Space

A few underpinnings of vector spaces are formally known, then again, actually it is conceivable that our own doesn’t know him by that name. For instance in three vectors I = (1, 0, 0) zeroing in on x-hub, j = (0, 1, 0) zeroing in on y-pivot, and k = (0, 0, 1) focused. close to the hub of z together from the ordinary design of every vector (x, y, z) inside is an uncommon mix of one line of standard fundamental vectors.

Definition

An (ordered) subset of a vector area V is a (proposed) premise of V if each vector v is authorized in V interestingly, may be represented as a linear mixture of vectors from β

\begin{equation}
V=v_{1} b_{1}+v_{2} b_{2}+v_{3} b_{3}+\cdots v_{n} b_{n}
\end{equation}

For a asked basis, the coefficients on this linear mixture are called the coordinates of the vector as for β.Later, while we observe arrays in extra detail, we can compose the coordinates of a vector v as a phase vector and provide it a unique notation.

\begin{equation}
v_{1}=\begin{aligned}
&1 \\
&2
\end{aligned}
\end{equation}
\begin{equation}
\begin{array}{r}
\mathbf{1} \\
v_{2}=\mathbf{0} \\
\mathbf{2}
\end{array}
\end{equation}

\begin{equation}
v_{3}=\begin{aligned}
&1 \\
&1 \\
&0
\end{aligned}
\end{equation}

THE VECTOR:

\begin{equation}
V=\begin{array}{r}
2 \\
1 \\
5
\end{array}
\end{equation}

is the linear combination of vectors v1, v2, v3, we can find real number a1,a2 and a3 so that

\begin{equation}
V=a_{1} v_{1}+a_{2} v_{2}+a_{3} v_{3}
\end{equation}

By subtracting we get

\begin{equation}
a_{1}\left[\begin{array}{l}
1 \\
2 \\
1
\end{array}\right]+a_{2}\left[\begin{array}{l}
1 \\
0 \\
2
\end{array}\right]+a_{3}\left[\begin{array}{l}
1 \\
1 \\
0
\end{array}\right]=\left[\begin{array}{l}
2 \\
1 \\
5
\end{array}\right]
\end{equation}
\begin{equation}
\begin{aligned}
a_{1}+a_{2}+a_{3} &=2 \\
2 a_{1}+a_{3} &=1 \\
a_{1}+2 a_{2} &=5 .
\end{aligned}
\end{equation}

By solving it we get the equations we get values a1= 1, a₂ = 2, and a₃ = – 1, which means that V is a linear combination of V_I, V₂, and V₃. Thus

\begin{equation}
\mathbf{v}=\mathbf{v}_{1}+2 \mathbf{v}_{2}-\mathbf{v}_{3}
\end{equation}

The Figure mentioned below show the linear combination of v1, v2, v3:

LINEAR INDEPENDENCE:

DEFINATION:

The vectors V1, V2 ……. Vt in a vector space V are called linearly dependent if there is one constants a1, a2, ……at, not all zero, so that

\begin{equation}
\sum_{j=1}^{k} a_{j} \mathbf{v}_{j}=a_{1} \mathbf{v}_{1}+a_{2} \mathbf{v}_{2}+\cdots+a_{k} \mathbf{v}_{k}=0
\end{equation}

Otherwise, V1, V2 …., Vk are known as linearly impartial. That is, V1, V2… Vk are linearly impartial if, each time a1V1 + a2V2 + … + akVk = 0,

a1 = a2 =……. = ak = 0.

If S = {V1, V₂,……,V_d },then we additionally say that the set S is linearly based or linearly impartial if the vectors have the corresponding property.

Example of Lineal Dependence

Determine whether the given vectors are linearly independent or not?

$$
\begin{gathered}
\mathbf{v}_{1}=\left[\begin{array}{l}
3 \\
2 \\
1
\end{array}\right], \quad \mathbf{v}_{2}=\left[\begin{array}{l}
1 \\
2 \\
0
\end{array}\right], \quad v_{3}=\left[\begin{array}{r}
-1 \\
2 \\
-1
\end{array}\right] \\
a_{1}\left[\begin{array}{l}
3 \\
2 \\
1
\end{array}\right]+a_{2}\left[\begin{array}{l}
1 \\
2 \\
0
\end{array}\right]+a_{3}\left[\begin{array}{r}
-1 \\
2 \\
-1
\end{array}\right]=\left[\begin{array}{l}
0 \\
0 \\
0
\end{array}\right] \\
3 a_{1}+a_{2}-a_{3}=0 \\
2 a_{1}+2 a_{2}+2 a_{3}=0 \\
a_{1}-a_{3}=0
\end{gathered}
$$
The desired augmented matrix is
$$
\left[\begin{array}{rrr:r}
3 & 1 & -1 & 0 \\
2 & 2 & 2 & 0 \\
1 & 0 & -1 & 0
\end{array}\right]
$$
The reduced row echelon form of the matrix is
$$
\left[\begin{array}{rrr:r}
1 & 0 & -1 & 0 \\
0 & 1 & 2 & 0 \\
0 & 0 & 0 & 0
\end{array}\right]
$$

Thus solution of matrix is non trivial

\begin{equation}
\left[\begin{array}{c}
k \\
-2 k \\
k
\end{array}\right], \quad k \neq 0 \text { (verify), }
\end{equation}

So the given matrix are linearly dependent.

Example:

Are the vectors

\begin{equation}
V_{1}=\left[\begin{array}{llll}
1 & 0 & 1 & 2
\end{array}\right] \quad V_{2}=\left[\begin{array}{llll}
0 & 1 & 1 & 2
\end{array}\right] \quad \text { and } \quad V_{3}=\left[\begin{array}{llll}
1 & 1 & 1 & 3
\end{array}\right]
\end{equation}

Linearly dependent or linearly independent?

\begin{equation}
\begin{aligned}
a_{1}+a_{3} &=0 \\
a_{2}+a_{3} &=0 \\
a_{1}+a_{2}+a_{3} &=0 \\
2 a_{1}+2 a_{2}+3 a_{3} &=0
\end{aligned}
\end{equation}

The desired augmented matrix is:

$$
\left[\begin{array}{lll:l}
1 & 0 & 1 & 0 \\
0 & 1 & 1 & 0 \\
1 & 1 & 1 & 0 \\
2 & 2 & 3 & 0
\end{array}\right]
$$
The reduced row echelon form of matrix is:
$$
\left[\begin{array}{lll:l}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0
\end{array}\right]
$$
Thus the only solution is the trivial solution $\mathrm{a}_{1}=\mathrm{a}_{2}=\mathrm{a}_{3}=0$, so the vectors are linearly independent.

VECTOR ROW DEPENDENCY TEST:

There are numerous circumstances where we might wish to know whether the Carrier Agreement is linearly free, that is to say, when one vector is a blend of another. Two vectors u and v are autonomous of line on the off chance that the indivisible numbers x and y fulfill xu + yv = 0 say x = y = 0.

$$
\begin{aligned}
\vec{u} &=\left[\begin{array}{l}
a \\
b
\end{array}\right] \\
\vec{v} &=\left[\begin{array}{l}
c \\
d
\end{array}\right]
\end{aligned}
$$
$\mathbf{x u}+\mathrm{y} \mathbf{v}=0$ is equivalent to
$$
0=x\left[\begin{array}{l}
a \\
b
\end{array}\right]+y\left[\begin{array}{l}
c \\
d
\end{array}\right]=\left[\begin{array}{ll}
a & c \\
b & d
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]
$$

For the situation where u and v are linearly autonomous, the principal reply for this plan is mathematical articulations is the inconsequential arrangement, x=y=0. This occurs in homogeneous frameworks if and provided that the determinant isn’t zero. We have now found a test to see if a given arrangement of vectors is linearly free: A bunch of n vectors of length n is linearly autonomous in the event that the grid with these vectors as segments has a non-zero determinant. The set is clear reliant assuming the determinant is zero

Conclusion

From this research we have reasoned that the vectors would be linearly dependent if the arrangement of vectors could be having a non-paltry linear mix of the vectors that would be equivalent to the zero and moreover they would be linearly independent if they could have an inconsequential linear blend of the vectors that would be equivalent to zero and a linear mix can be finished up for instance assuming we are having a mix of certain vectors and their linear mix can just be settled by utilizing two procedures possibly we essentially add them or utilize scalar multiplication the scalars are generally be called by the name of “weights”.

What is Linear combinations, Linear dependence and Linear Independence?