Introduction
In this article, I will discuss the shortcuts for finding the determinant of a matrix. Determinant has great significance in linear algebra. There are many practical problems that can be modeled as a linear system. When the systems are modeled as linearly:
AX=B
then the next step is to solve it. One way is to apply the Cramer’s rule that involves finding the determinants.
It is always easy to find the determinant of a 2X2 or 3X3 matrix. But when the order of the system increases, then it becomes cumbersome to find the determinant of it.
Ways to find a determinant
The first method is to expand the matrix by its first row or column in terms of its coefficients and minors. Lets do an example
e.g.,
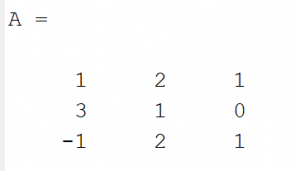
Expanding it by row 1, we get
=1[1-0]-2[3-0]+1[6+1]
=1(1)-2(3)+1(7)
=1-6+7
=2
Sarru’s Method for finding the determinant
In this method we write the first columns except the last one again and then join the diagonal entries just like shown below. The diagonals going down are written with the positive sign (starting from left that is marked in red) and the diagonals gong up that are marked in blue are written with negative sign and finally we simplify the expression.
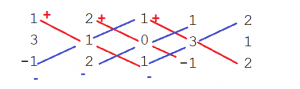
=1+0+6-(-1)-0-6
=2
Example of Sarru’s Method
Properties of determinant
There are several properties of determinant that are discussed below:
- The determinant of the identity matrix is always equal to 1.
- If two rows are interchanged then det(A)=-det(A).
- If any row of a matrix is equal to zero, then determinant is zero.
- If two rows of a matrix are same/ identical then determinant is zero.
- If we add the multiple of one row into another row then determinant remains unchanged.
- det(A-1)= 1/det(A)
- det(AB)=det(A).det(B)
- det(A2)= det(A). det(A)
- for an mxn matrix, det(2A)=(2m)det(A)
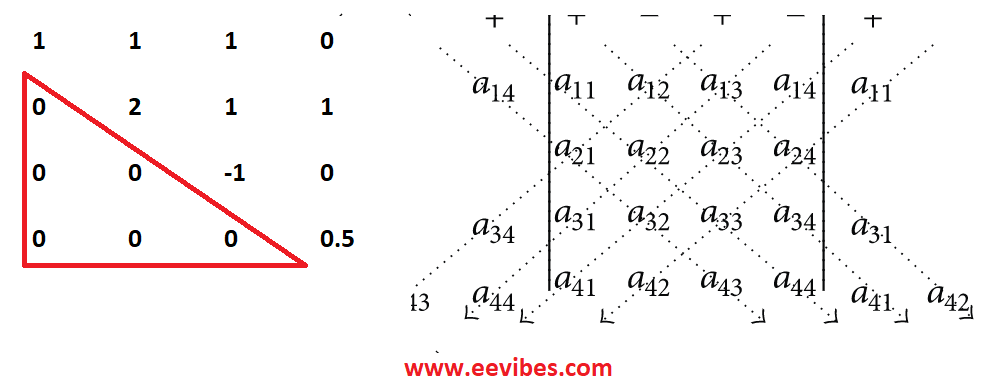
- The determinant of a triangular matrix is equal to the product of entries on the main diagonal.
How to find the determinant of higher order matrices?
In order to find the determinant of higher of higher order matrices, first you need to see either the given matrix follows any of the properties mentioned above? If so, then that would be quite easy to find the answer.
Most common method that is used these days is to convert the given matrix into an upper triangular matrix using the Gauss Elimination and then multiply all the entries on the main diagonal.
Example
Find the determinant of a 4×4 matrix

Solution

Now just multiply the diagonal entries and hence determinant of it is=(1)(2)(-1)(0.5)=-1.
Also read here