Types of Tree Traversal
Different Types of Tree Traversal. In data structure traversing the tree mean visiting each node in a particular manner. A binary tree is well known data structure where each node can have maximum of two nodes. Level order traversal is used for determining the depth between two nodes. Trees can be represented in the forms of array but for memory optimization purpose, we prefer to use structures and pointer form representation.
There are two types of tree traversal:
- Depth First Traversal
- Breadth First Traversal
- Pre-order Traversal
- Post-order Traversal
- In-order Traversal
Breadth First Traversal
It is also known as the level order traversal. Consider the following tree for understanding how Breadth First Traversal works.
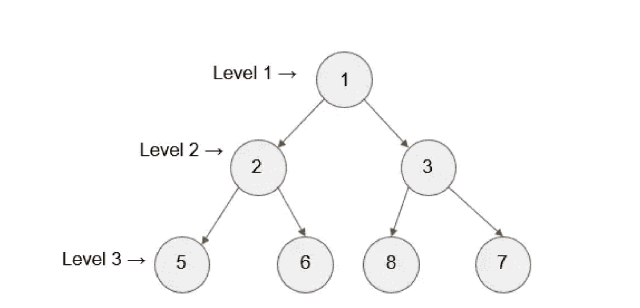
We will start from the root node 1 and it will be marked as level 1. Then we visit all the children of the root node in this algorithm. For this case, we will visit node 2 and 3 and mark it as level 2. Here are two nodes at level 2. All the children of nodes at level 2 will be visited now and hence we will mark this level as level 3.
We can simply represent this relation by using the following formula:
Level of node= Parent’s node level+1
The Pseudo code for level order traversal is given below:

In-order Traversal Binary Tree
In order traversal visits the left subtree first, then root (Parent Node) , and finally the right subtree. It can be remembered simply that way: (LPR)
We will consider the same example that we did previously. So, lets say that the Parent node is 1.
Visit the left subtree of node 1 which is 2 in this example as highlighted with red box in figure below:
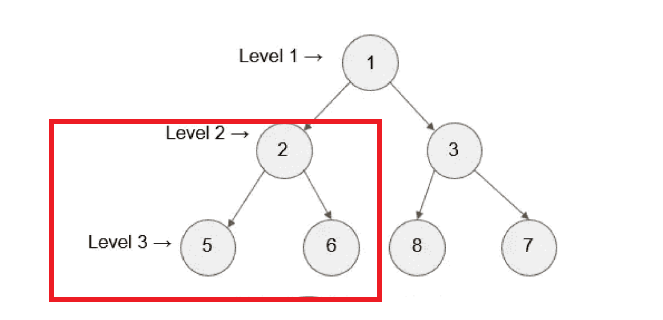
The current node will become now 2 as it is the left subtree. According to the LPR rule the next node will be 5. As 5 it has no more children s it will be marked as visited. Then 2 will be marked as visited node after sending 5. Now as per the sequence of LPR, the right node which is 6 will be visited. Hence the whole left subtree is visited. Now after visiting the left subtree, the parent node which is 1 will be visited.
After that we will move to the right subtree that is shown below:
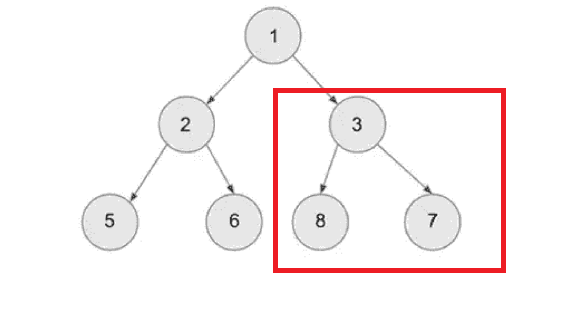
Here, the node 3 has left node 8 so it will be visited first, then 3 (parent node) and finally nod 7 will be visited.
The In-order Traversal Binary Tree will be like:
5-2-6-1-8-3-7
Here is the pseudo code for in-order tree traversal:

Post-Order Tree Traversal
In this traversal we first perform the left subtree traversal, then right subtree traversal after the root. Consider the following diagram:
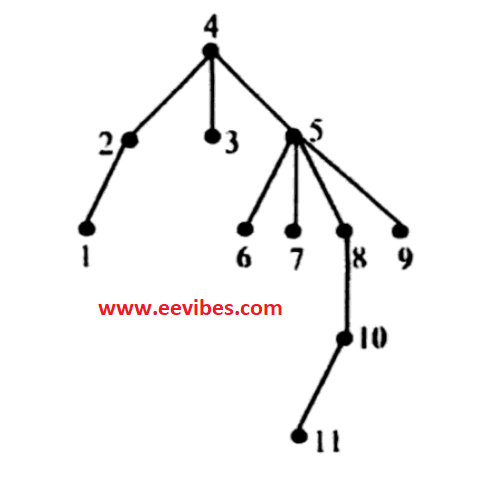
In this case 4 is the root and 2,3,5 are the children. The postorder traversal of this tree is:
1—2—-3—-6—7—-11—-10—-8—-9—-5—–4
The postorder numbering can be found using Euler circuit.
Preorder Traversal (VLR)
The preorder traversal visits the node first, then left subtree and finally the right subtree. It starts with the root node. If the root has left subtree then it is preorderly traversed first and then proceeds towards the right subtree in the same manner.
The Pesudocode is shown below:

Example of Preorder Traversal
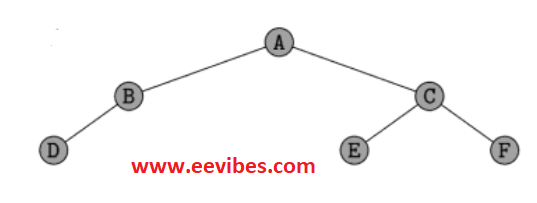
The preorder traversal will visit the root or vertex which is A in this case. Root has the left subtree so it will traverse the node B and then D. After completely visiting the left subtree, it will visit the node C, E and then F finally. The traversing path of preorder traverse is given below:
A–B—D—–C—-E—F
Aslo read here:
Adaptive Huffman Encoding in Data Compression | Unique Example