Drawback of Huffman Encoding

Adaptive Huffman Encoding in Data Compression | Unique Example. In Huffman encoding, it is necessary to already know the frequency or probabilities of source sequence. If it is unknown then Huffman encoding can be done is two passes:

In first pass, we calculate the statistics and in the second pass we encode the sequence. Faller and Gallagher developed adaptive algorithms to convert Huffman code into a single pass procedure based on the statistics of the symbols already encountered. Vitter and Knuth later on improved these algorithms. 

So, if we want to encode the (k+1)th symbol using the statistics of first k symbols, we could recompute the code using the Huffman coding procedure each time a symbol is transmitted.

However, this approach was not much appreciated because large computational was involved in it. Hence, the adaptive Huffman encoding scheme was introduced. 

Adaptive Huffman Encoding

Huffman encoding scheme is described in terms of the binary tree. We use squares for representing the external nodes or leaves and they correspond to the symbols in the source alphabets. The codewords assigned to each symbol can be determined by traversing the tree from root to leaf or node. Since it is a binary tree so we use 0 for the left branch and 1 for the right branch. 

Now if we add two other parameters to this binary tree:

1. The weight of each leaf which is actually the number we write inside each node.
2. A node Number. 

The weight of each external node represents the frequency or number of times a symbol is encountered in the list. The weight of internal nodes is equal to the summation of weights of  its offspring nodes. The node number that we assign to an external and internal node is a unique number y_i. 

Sibling Property of nodes in Huffman Coding

If the size of alphabet is n, then 2n-1 internal and external nodes can be numbered as y₁,y₂, y₃,……….., y_{2n-1. Also} y_j  y_{j+1 are offspring of same parent node or siblings and the node number will always be greater than this. These two properties are called the sibling property. Any tree possessing this property is called the Huffman Tree.} 

Adaptive Huffman Coding Procedure

In adaptive Huffman coding procedure, the statistics of  source sequence are unknown both at the transmitter and the receiving side. The three at the start of algorithm on both sides: transmitter and receiver start with a single node. This node is called “NOT YET TRANSMITTED (NYT)” node and its weight is 0.

As the transmission begins, nodes corresponding to the symbols are added in the tree and then an update procedure begins. In this way the tree is reconfigured.

Adaptive Huffman Encoding with Data Compression | Unique Example

How to Assign the Codes in Huffman Coding Scheme?

Before the beginning of transmission, a fixed code for each symbol is agreed upon between transmitter and receiver. A simple (short) code is as follows:

If size of the source alphabet is m (a₁, a₂, a₃,……….., a_n) then we choose e and r such that m=2^e+r. The range of r is given as: 

For encoding a letter a_k we first check the range of k. If k lies in the range:

then a_k is encoded as e+1 bit binary representation of k-1. Otherwise we encode a_k as e-bit binary representation of k-r-1. 

Example of Fixed Code Assignment

For example, suppose m = 26, then e = 4, and r = 10. The symbol a₁ is encoded as 00000, the symbol a₂ is encoded as 00001, and the symbola₂₂ is encoded as 1011. When a symbol is encountered for the first time, the code for the NYT node is transmitted, followed by the fixed code for the symbol. A node for the symbol is then created, and the symbol is taken out of the NYT list.

The transmitter and receiver begin with the same tree structure. The updating procedure also follows the same step. Hence encoding and decoding procedure is synchronized. 

Update Procedure in Huffman Coding

The nodes should be in the fixed order before starting the update procedure which is preserved by numbering the nodes. We assign the largest number to the root and smallest number to the NYT node.

If we start from the NYT node and move towards the root then numbers are assigned in the increasing order, moving from left to right. The updating procedure is shown in the figure below:

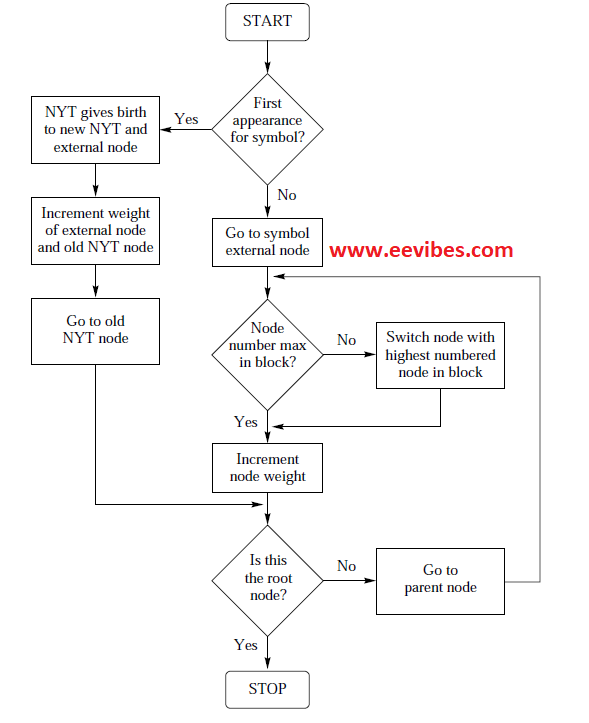
The purpose of update procedure is to preserve the sibling property. This procedure follows the same step at the transmitter and receiver when a symbol is encoded and decoded.

Steps in the Update Procedure

Once we encode a symbol, then we examine the external node corresponding to the symbol in the same block to check either it has the largest block number or not.

If the external node does not have the largest node number in the block, we will exchange it with the largest node number in the same block. We will continue it as long as the node with the higher number is not the parent of the node being updated. Then we increment the weight of external node.

If we did not exchange the nodes before the weight of the node is incremented, it is very likely that the ordering required by the sibling property would be destroyed. Once we have incremented the weight of the node, we have adapted the Huffman tree at that level.

We then turn our attention to the next level by examining the parent node of the node whose weight was incremented to see if it has the largest number in its block. If it does not, it is exchanged with the node with the largest number in the block.

Again, an exception to this is when the node with the higher node number is the parent of the node under consideration.

Once an exchange has taken place (or it has been determined that there is no need for an exchange), the weight of the parent node is incremented. We then proceed to a new parent node and the process is repeated. This process continues until the root of the tree is reached.

If a new symbol arrives for encoding or decoding, a new external node is assigned to the symbol and an NYT node is appended. They both are the offspring of old NYT.

We increment the weight of the new external node by one. As the old NYT node is the parent of the new
external node, we increment its weight by one and then go on to update all the other nodes until we reach the root of the tree.

Encoding Procedure of Adaptive Huffman

The following figure shows the flowchart of Adaptive Huffman encoding scheme.

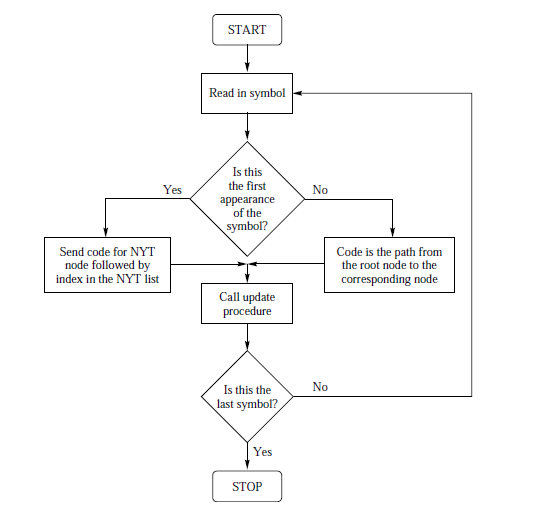
Initially we will have a single node, both at the encoding and decoding side which is called the NYT node. Therefore, a fixed code is assigned to the first encountering symbol. After that, when the next symbol arrives we assign it NYT code followed by the fixed code agreed-upon initially.

NYT code is obtained by traversing from the root to the NYT node. This alerts the receiver to the fact that the symbol whose code follows does not as yet have a node in the Huffman tree.

If the encountered symbol is already present in the tree, its node must be present already and we will just increment in its value by one and will assign the code by traversing from the root to that node.

Adaptive Huffman Coding Unique Example| Part 1

Adaptive Huffman Coding Unique Example| Part 2