Limits of Maxwell’s Equations
What are the Limitations of Maxwell’s Equations? Maxwell’s equations may have survived unscathed through the revolution of relativity; but the theory did not survive the discovery of quantum physics. The development of quantum physics have shown that Maxwell’s equations are an approximation, albeit a very good one. For many applications Maxwell’s suffice.
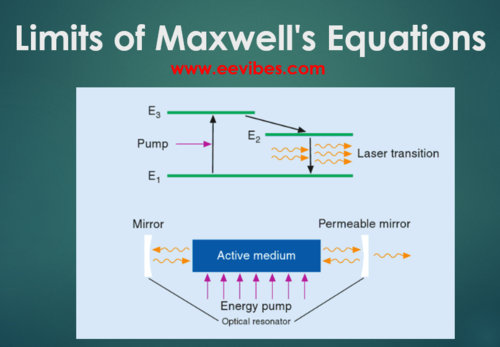
In addition to not being able to correctly predict the observations of quantum phenomenon such as thermal radiation and the operation of the laser, there is one inherit consistency in Maxwell’s equations. This inconsistency involves the self force of a charge and still has no known solution.
When a charge is accelerated, it radiates energy. The radiation energy comes from the force that causes the charge to move. For instance, imagine you have a charged ball and you move it back and forth. You must provide extra energy to move the field, which is observed as radiation.
Because energy is required to move the field, the filed has mass or inertia associated with it. The field mass is in addition to the mass of particle itself (i.e., the mass that particle would have were if not charged). Furthermore, since you must provide a force to move the field, the field must produce an equal but opposite force on you, as acquired by Newton’s third law.
How does the field convey this force?
The field is a distributed entity. How can it produce and immediate and concentrated force on you, the source of the force? One way around this problem is to suppose that when the charge is accelerated, it encounters its own retarded or delayed field. The interaction of the charge with its own field causes a force to act back upon the charge and consequently a force acts upon you.
This theory is in fact reasonable, but it causes other problems. Instead of talking about an arbitrary charge, consider an electron, the fundamental charge of nature. If the electron is assumed to be of finite, non-zero dimensions, then under acceleration different parts of the electron would feel different amounts of force, and the electron would deform.
The internal structure of electron becomes unstable unless another, non-electromagnetic, force is invented to hold it together and to maintain its shape and size. To get around this problem, the electron can be assumed to be a point particle with no size or dimension. However, assuming that the electron is a point particle causes a slew of additional difficulties such as infinite charge density and the existence of simple problems that have either multiple solutions or no mathematical solutions. The only known way out of this dilemma is through quantum electrodynamics.
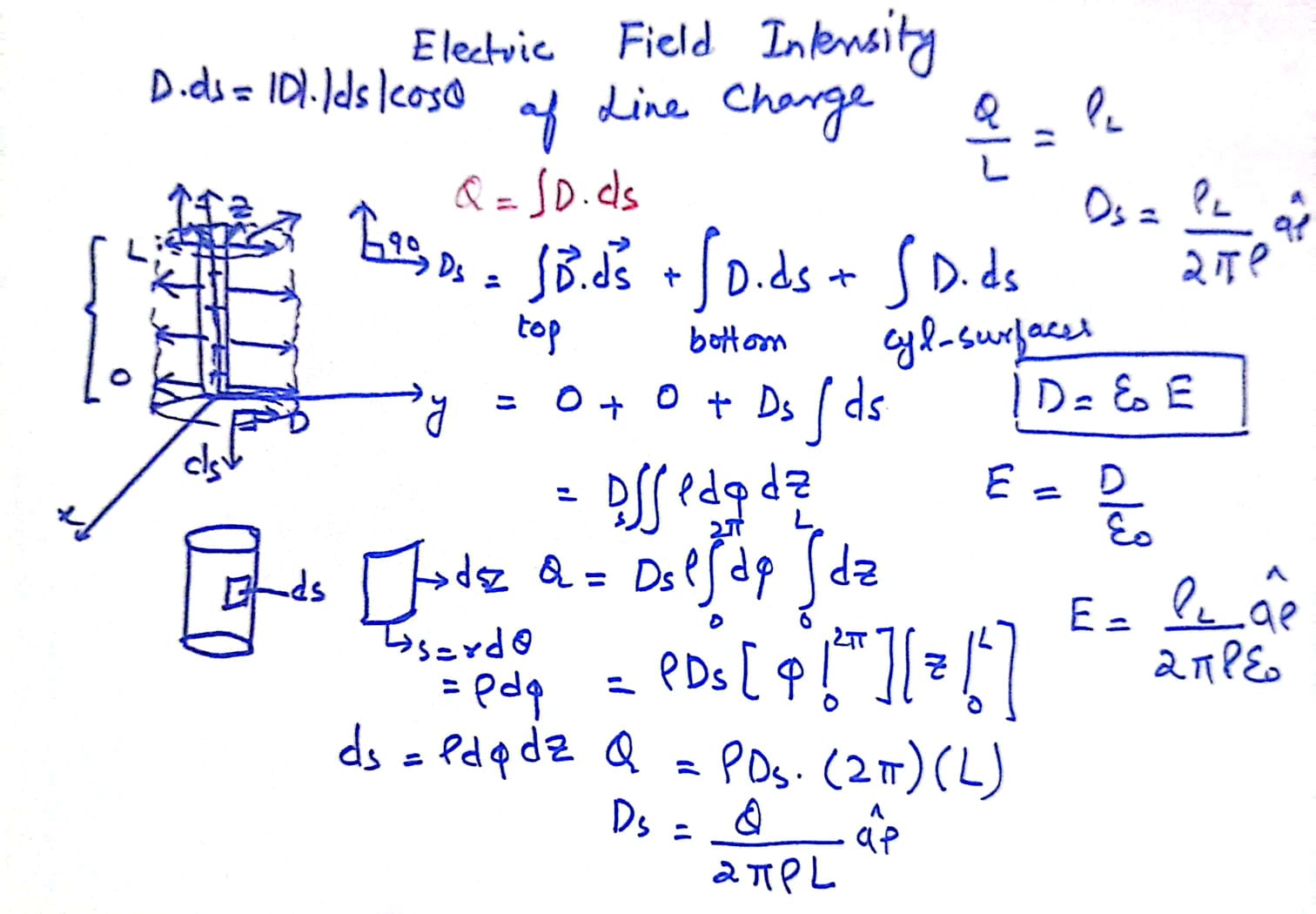
Application of Gauss’s Law for Calculating the Electric Field Intensity of a Line Charge
Also read here: