Table of Contents
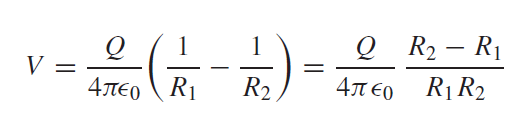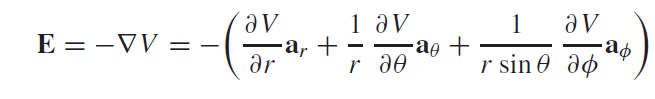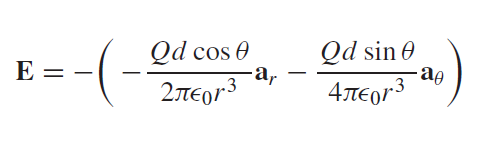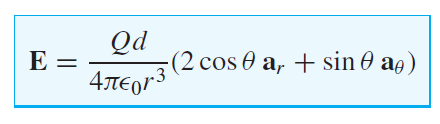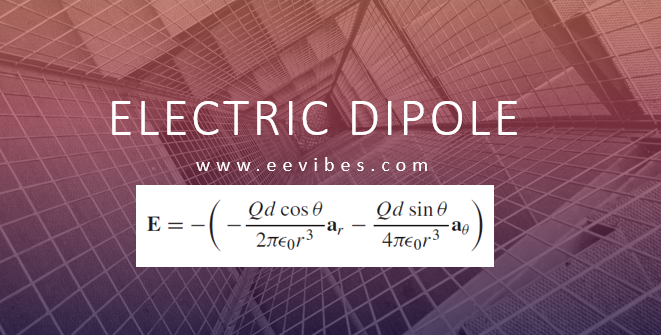
Introduction to Electric Dipole
What is an Electric Dipole? In order to understand the basis of behavior of dielectric materials in electric field, dipole fields are used. Dipole fields are also helpful for understanding the concept of imaging. When the two point charges of equal magnitude but of opposite signs are separated by the distance that is small as compared to the distance at which we want to measure the electric filed and potential, form a dipole. The electric dipole is shown in the figure below.
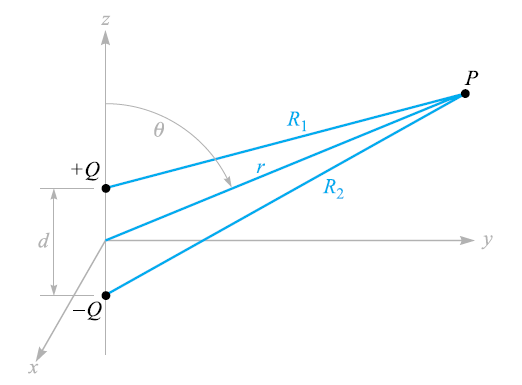
The point P will have its components in spherical coordinates r, θ, and φ = 90◦. It can be seen that the positive and negative charges are placed at the distance (0,0,1/2d) and (0,0,-1/2d) respectively. If we want to evaluate E first, then we need to find two components of E and φ component will be zero because of symmetry.
The electric potential V can be found by using the line integral of E considering the initial point is taken at infinity.
On the other hand determination of V is relatively easy first. This is because the potential is found as a function of position by simply adding the scalar potentials from two different charges. The direction of E is found as the negative of Gradient of V.
Considering the distance from Q1 and Q2 to point P as R1 and R2, we calculate the total potential as:
Note that the plane z = 0, midway between the two point charges, is the locus of points for which R1 = R2, and is therefore at zero potential, as are all points at infinity.
For a distant point, R1 =R2, and the R1R2 product in the denominator may be replaced by r2. The approximation may not be made in the numerator, however, without obtaining the trivial answer that the potential field approaches zero as we go very far away from the dipole. Coming back a little closer to the dipole, we see from the figure below that R2 − R1 may be approximated very easily if R1 and R2 are assumed to be parallel,
Hence the final expression for the potential is:
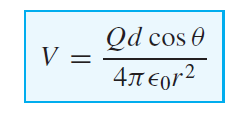If θ = 90◦ then electric potential becomes zero. Hence Z=0 is a zero potential plane. For finding the electric field intensity, we will take the gradient of the potential field V. Hence we have:
Finally we have
or
Also read here