What is Imaging?
In this article, we have explained about what is imaging? Since the focal point stands behind the lens, it is very easy to use lens for imaging. Suppose that you place a photographic plate in the plane of focal point as shown in the figure below.
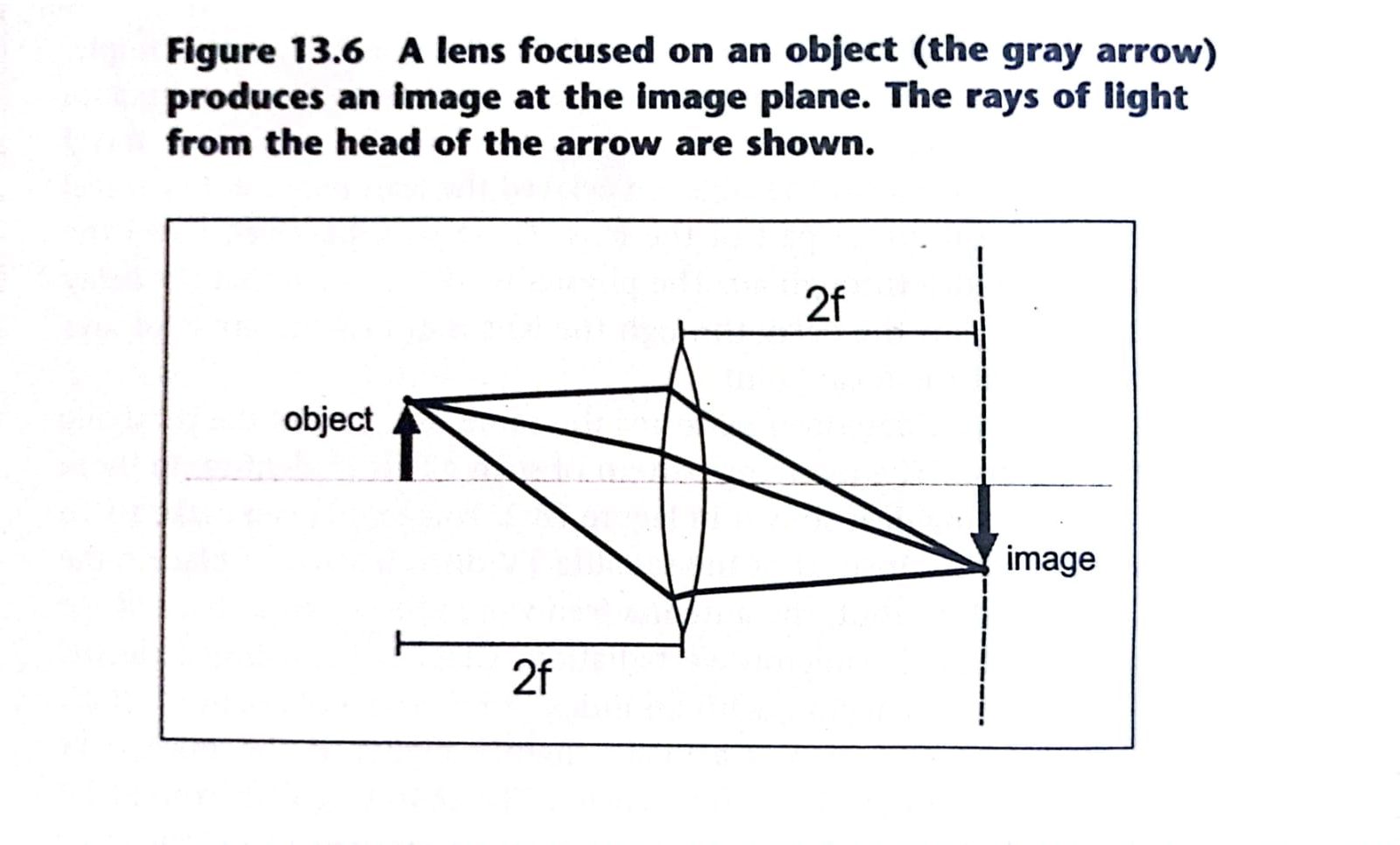
The plane where the plate is located is called the image plane. Assume that the diameter of the lens is of several wavelengths. Not only will rays perpendicular to the lens focus to a point at center of the image plane, but rays that arrive at slightly different angles will focus to points slightly offset from the center.
In fact, for every angle of incidence of a plane wave, there is corresponding point on the image plane where light from that direction will be focused. A photographic plate as well as the special receptor cells in our eyes can capture the light at all of the different image plane points simultaneously.
Thus, both systems (the camera and the eye) can produce images. The imaging system shown in the figure, which is focused at infinity, can be used to image objects at great distances such as stars in the sky or mountains in the distance.
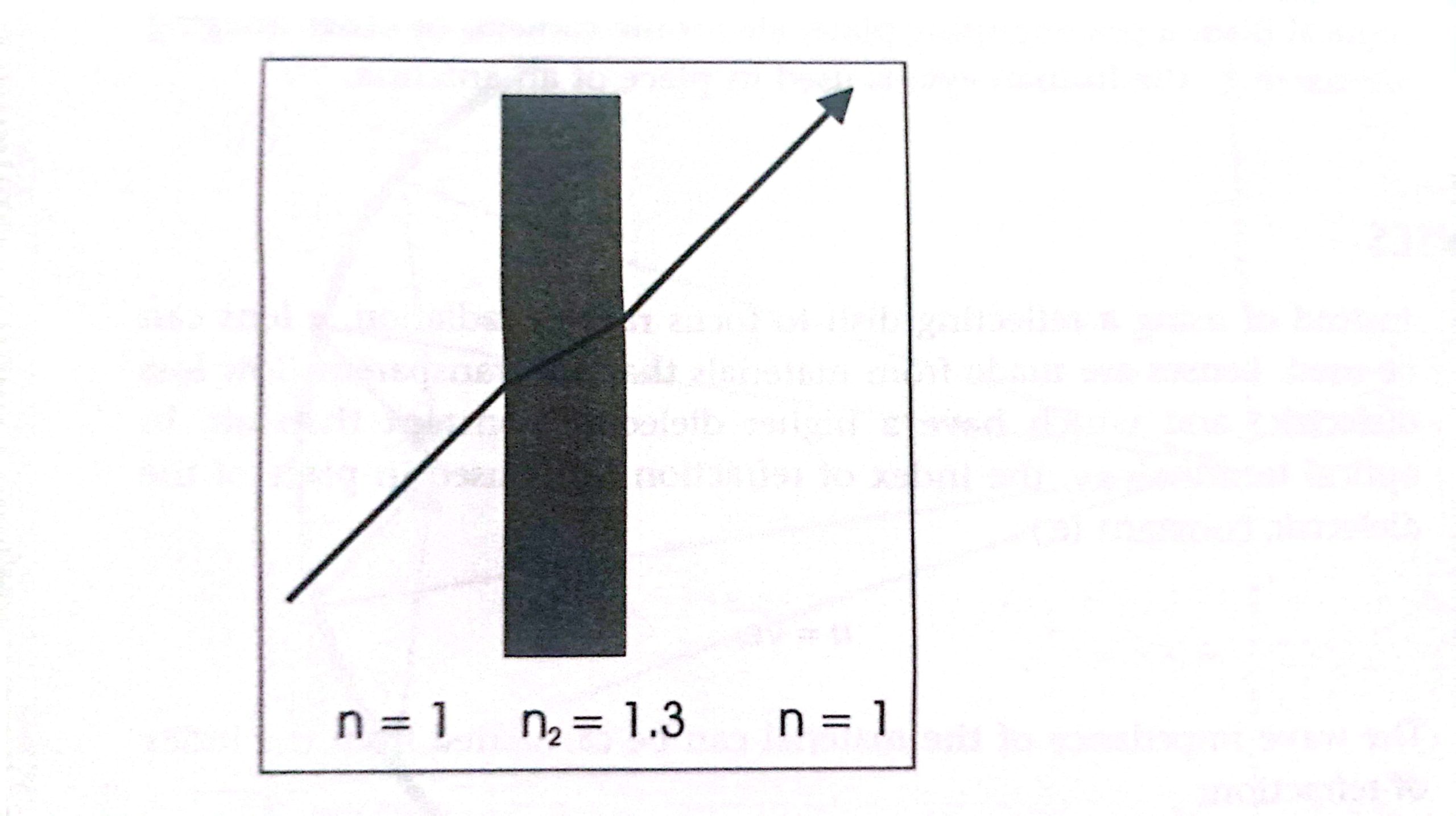
The distance, f, from the lens to the focal plane is a function of the lens material, index of refraction, and the shape of front and back surfaces of the lens.
In practice, lenses usually have spherical surface instead of parabolic surface because the spherical surface is easier to create. Some slight errors occur due to this shape. The focal length for thin spherical lens is a function of the radius of curvature of the two spherical surfaces, front and back.
Imaging is not limited to objects at very large and approximately infinite distances. Any imaging system can be easily changed to focus on near objects by increasing the distance from the lens to the imaging plane as shown below. This is how a camera is focused.
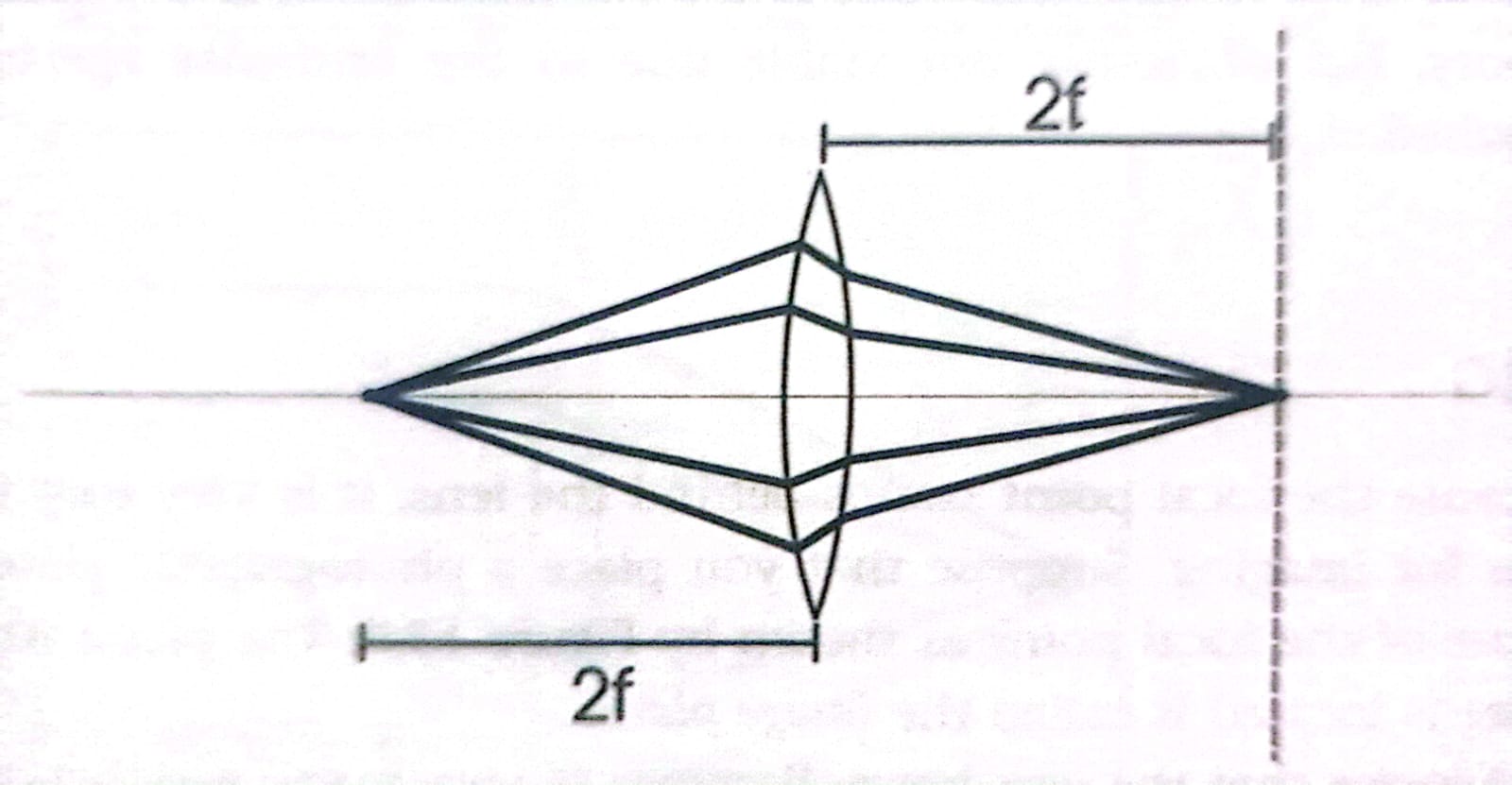
The lens is moved in relation to the imaging plane where the film resides. The human eye uses a different method to focus. The muscle of the eye can be tensed to change the shape of the lens, thus changing the focal properties of the lens.
What is Imaging Resolution?
All imaging devices are limited in the smallness and spacing of objects they can resolve. Objects smaller or more closely spaced than the device’s resolution become blurred. There are two limited factors of resolution. The first is the physical wavelength. Due to the phenomenon of diffraction, which is common to all wave types, you can not image smaller than about a half-wavelength in dimension. For this same reason transmitted wave energy is greatly diminished when incident upon the small apertures less than 1/2λ in both dimensions.
The waves cannot easily pass through such small opening. The complement to a small aperture is a small object. When waves are incident to a small disk, for instance, very little of the wave is reflected, The wave tends to diffract around the object instead. This property of waves defines the resolution limits for the microscopes.
Visible light microscopes can only resolve objects down to about one half of the shortest visible wavelength. The shortest visible waves are in the violet color range and have a wavelength of about 380 nm.
The same property limits the resolution of the photolithographic processes used in integrated manufacturing, although in the lithographic process radiation in the ultraviolet can be used because the process is not limited by the properties of human vision.
The second resolution limit is the angular resolution limit. The angular resolution limit defines how closely an imaging device can resolve two objects in terms of angular separation. The angular resolution of an imaging system is dependent on the electrical diameter of the aperture.
An aperture is in effect a window of the entire imaging signal. The resulting image is blurred in inverse proportion to the aperture’s electrical dimension. An aperture with an electrical radius tending to infinity produces an image tending to on finite resolution.
Angular resolution is defined by the Rayleigh criterion. The Rayleigh criterion defines the minimal angular resolution in terms of the electrical size of the aperture (e.g., lens, dish, or antenna array)
Ɵ=1.22/Dλ
where Dλ is the aperture diameter given in wavelengths. Smaller wavelengths and larger apertures provide better angular resolution. For this reason cameras with the larger lenses produce sharper images. This fact can be readily seen by examining the following figure.
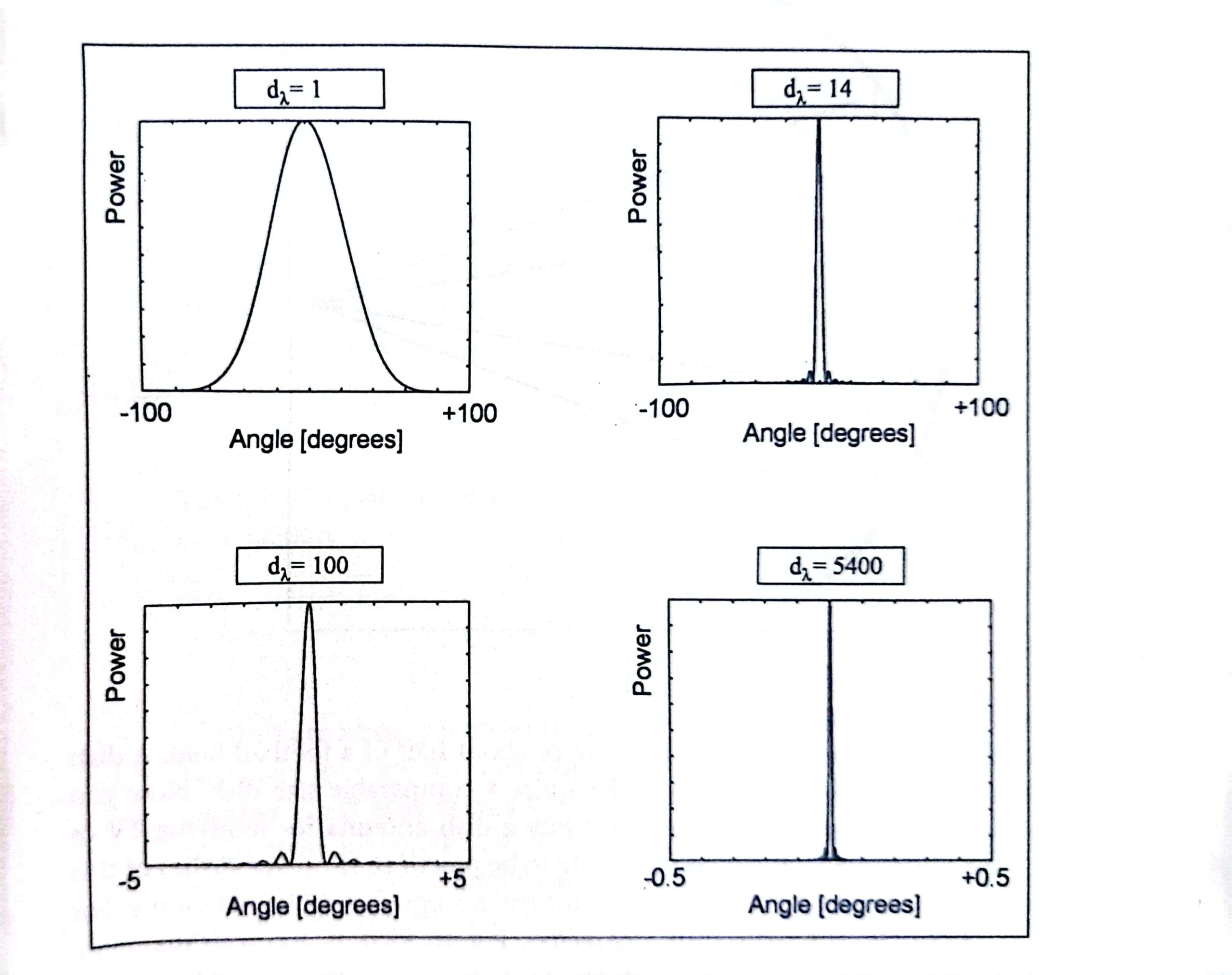
Apertures that are electrically larger produce sharper focal lobes. The human eye has an angular resolution of about 0.01 degrees. The angular resolution is what limits our vision in practice.
Larger telescopes have much larger optical apertures and can therefore provide much higher resolution images of the sky. Imaging becomes impractically large at radio frequencies. The eye has a diameter of about 5000 wavelengths. To create an image device of equal electrical diameter requires an aperture of diameter of 1600m at 100 MHz.
Microwaves can be used for imaging, but the resolution of the object it can measure is much less than in the optical range. Microwave imaging has several applications, including two dimensional radar imaging for aircraft identification. Traditional one dimensional radar just produces a single dot on the radar screen, whereas two dimensional radar produces an image of aircraft similar to a low resolution black and white photo.
Also read here: