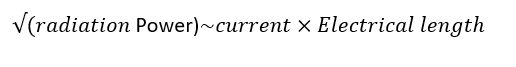The Electric Field of a Direct Current (DC)
The Electric Field of Direct Current (DC) and Alternating Current (AC). If a constant voltage is connected across a length of wire, the voltage will cause a proportional current governed by Ohm’s law (V=IR). The DC current travelling in a wire consists of the migration of electrons. Although the path of each individual electron is quite random and complex, the average movement of electrons, considered as a group, produces a constant drift of charge.
Therefore, at a microscopic level we can use an equivalent model that consists of fictitious charges travelling at a constant velocity, ignoring the specifics of each electron. Radiation, will not occur, because the effective charge is travelling at a constant velocity and experiences no acceleration. The following figure shows the electric field of DC current.
The randomness of the electron movement is caused by the collisions at atomic level. These fluctuations show up as noise in the circuit. These noisy variations of the individual electrons do in fact cause radiation, but due to the violent nature of the electron collisions, most of the radiation energy occurs in the infrared region, and is commonly known as heat radiation.
Some of this radiation is propagated at lower energies, in microwave and radio bands. The radio wave radiation shows up as white noise when received by an antenna because of its random nature.
Example
For example, when you tune your radio to a frequency where no broadcast is present, all you hear is the noise waves of thermal radiation.
The Electric Field of a Alternating Current (AC)
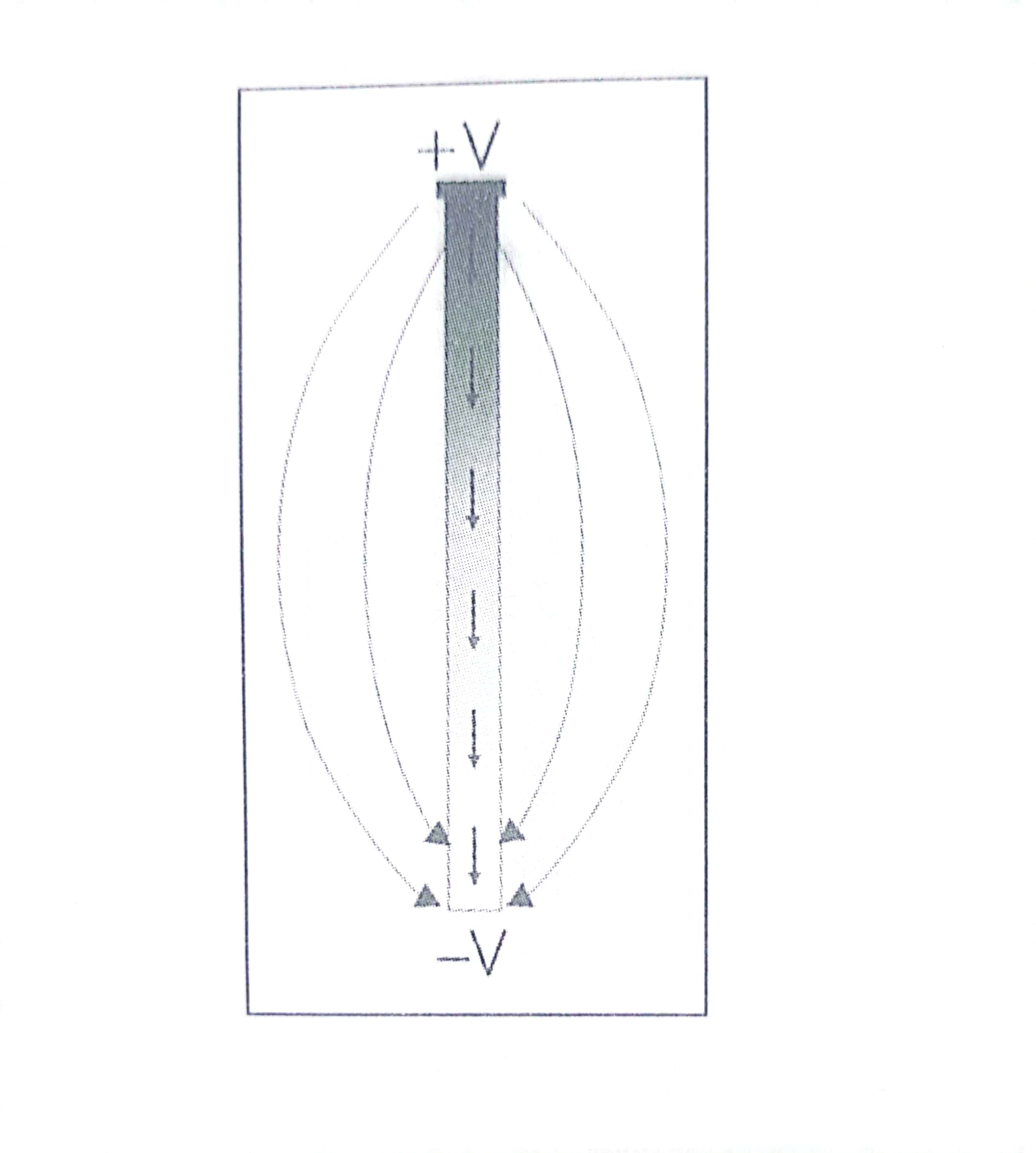
If we allow the voltage source across the wire to slowly oscillate in time at frequency,f0, the accompanying electric field will take the same form as that of the DC charge, except that the magnitude will vary between the positive and negative values.
If we relate frequency to the wavelength by λ=c/f, we define slow oscillation at any frequency whose corresponding wavelength is much greater than the length of the wire. This condition is often called quasi-static.
In this state, the current in the wire will vary sinusoidally, and the effective charge will experience a sinusoidal acceleration. As a result an oscillating charge will radiate the electromagnetic energy at the frequency f0.
The power (energy per time) radiated is proportional to the magnitude of the current squared and the length of the wire squared, because both parameters increase the amount of moving charge. The radiation power is also proportional to the frequency squared since the charge experiences a greater acceleration at higher frequencies.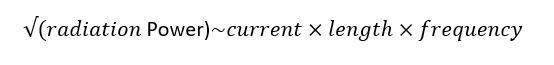
This expression shows why RF signals radiate more readily than the signals at lower frequencies such as those in the audio range. In other words, a given circuit will radiate more at higher frequencies. Because there is inverse relation between wavelength and frequency. An equivalent expression for the above one can be written as:
Hence at a given source voltage and frequency, the radiated power is proportional to the length of the wire squared. In other words, the longer you make an antenna the more it will radiate.
So far we have considered slowly oscillating fields. When the frequency of oscillating voltages is increased such that the wavelength approaches the length of the wire or less, the quasi-static picture no longer holds true. As shown in the following figure, the current is no longer equal throughout the length of the wire. In fact, the current is pointing in different directions at different locations.
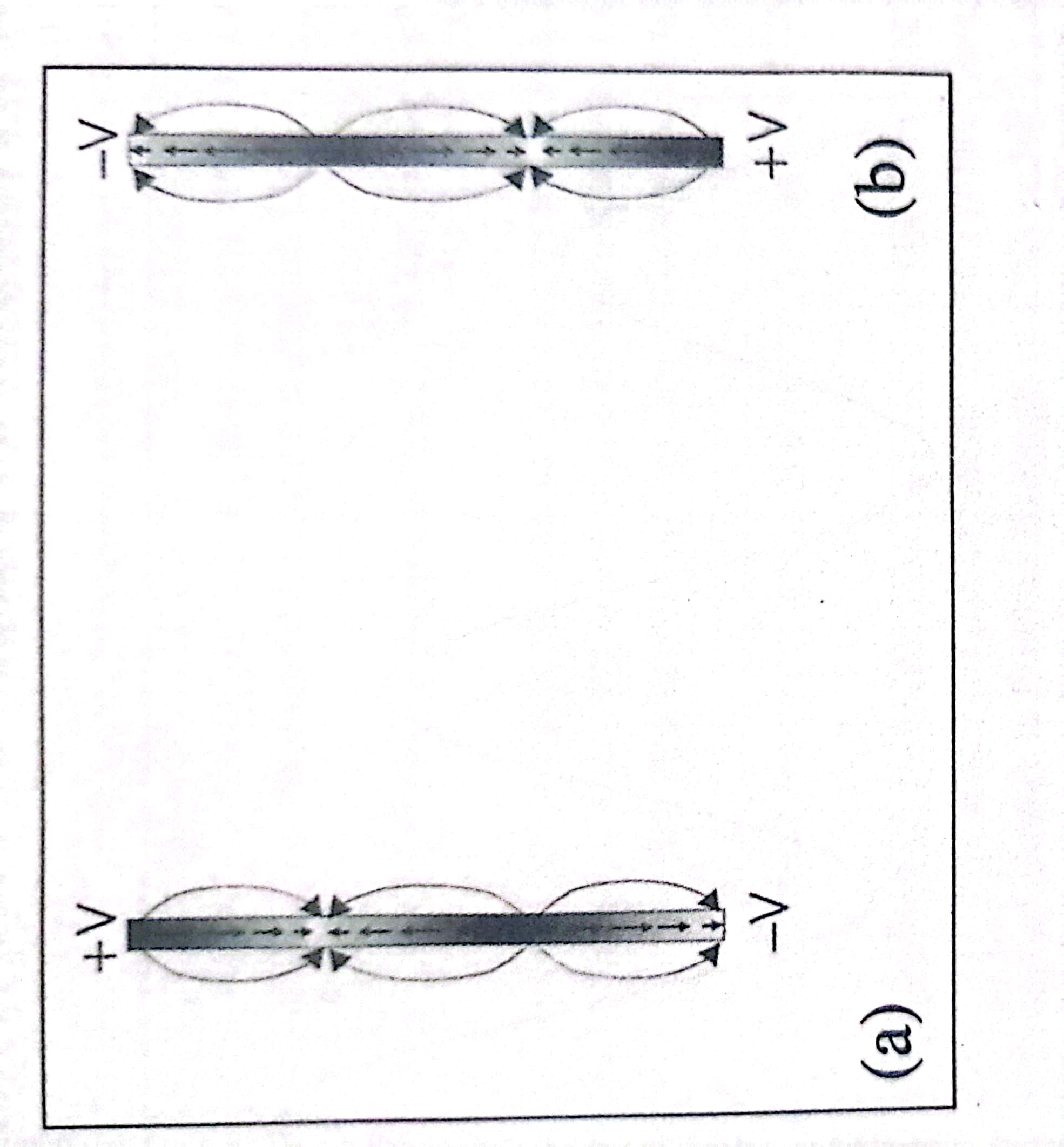
These opposing currents cause destructive interference just as water waves colliding from opposite directions tend to cancel out the effect of each other. The result is that the radiation is no longer directly proportional to the wire or antenna length squared.
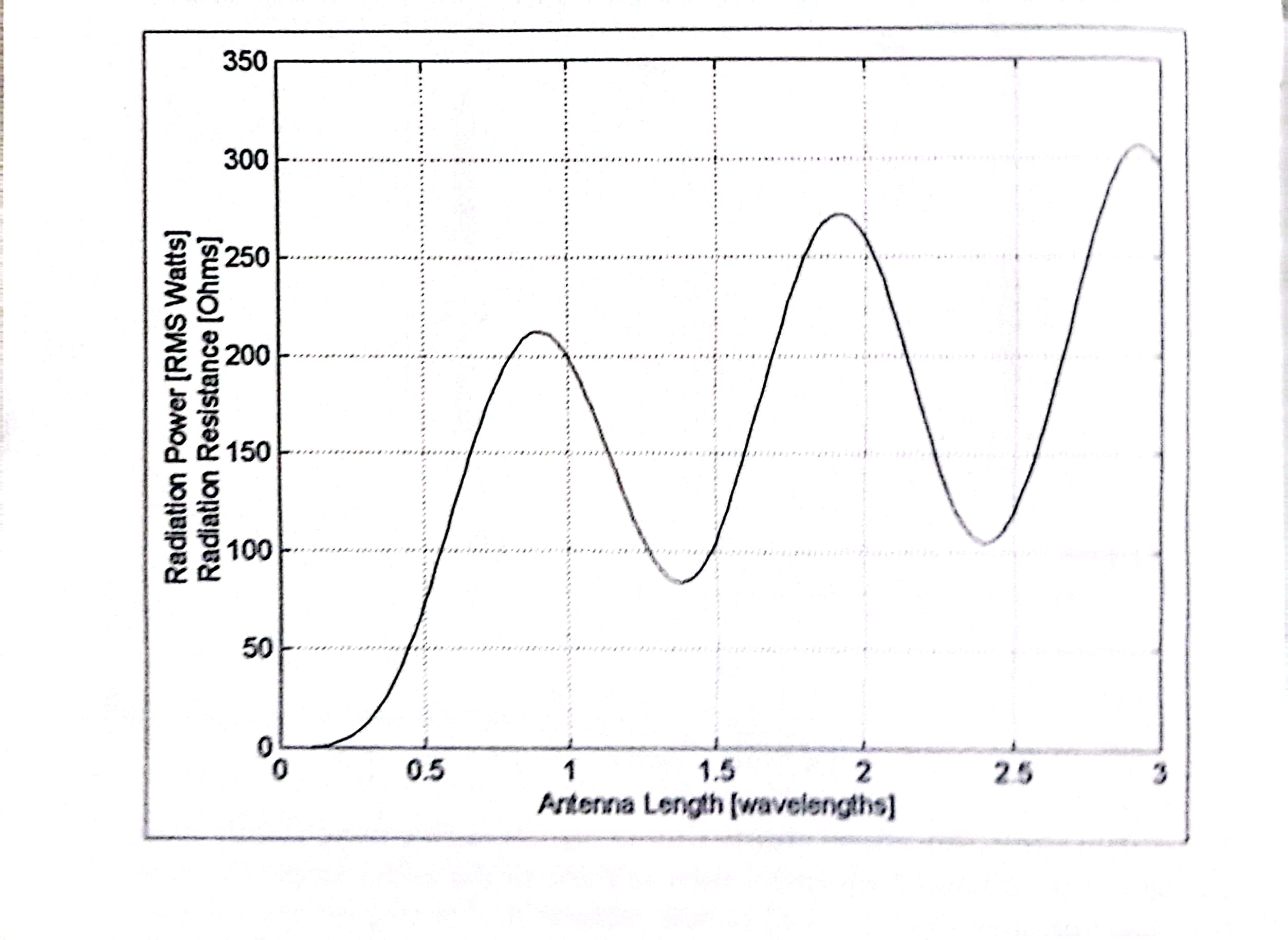
Above figure shows a plot of radiated power as a function of antenna length. When an antenna is much smaller as compared to wavelength, the radiation power is proportional to the length squared. However, for wire lengths near or above the wavelength, the radiated power relates as a slowly increasing and oscillating function.
This “diminishing returns” of the radiation power versus wire length is one of the reasons that λ/2 is usually chosen as the length for dipole antenna. (λ/4 for a monopole). The other reasons being that at length=λ/2, the electrical impedance of the antenna purely real (electrically resonant), and the radiation pattern is simple (single lobed) and broad.
Drill 2.6
Three infinite uniform sheets of charge are located in free space as follows: 3 nC/m2 at z = −4, 6 nC/m2 at z = 1, and −8 nC/m2 at z = 4. Find E at the point: (a) PA(2, 5,−5); (b) PB(4, 2,−3); (c) PC(−1,−5, 2); (d) PD(−2, 4, 5).
Solution
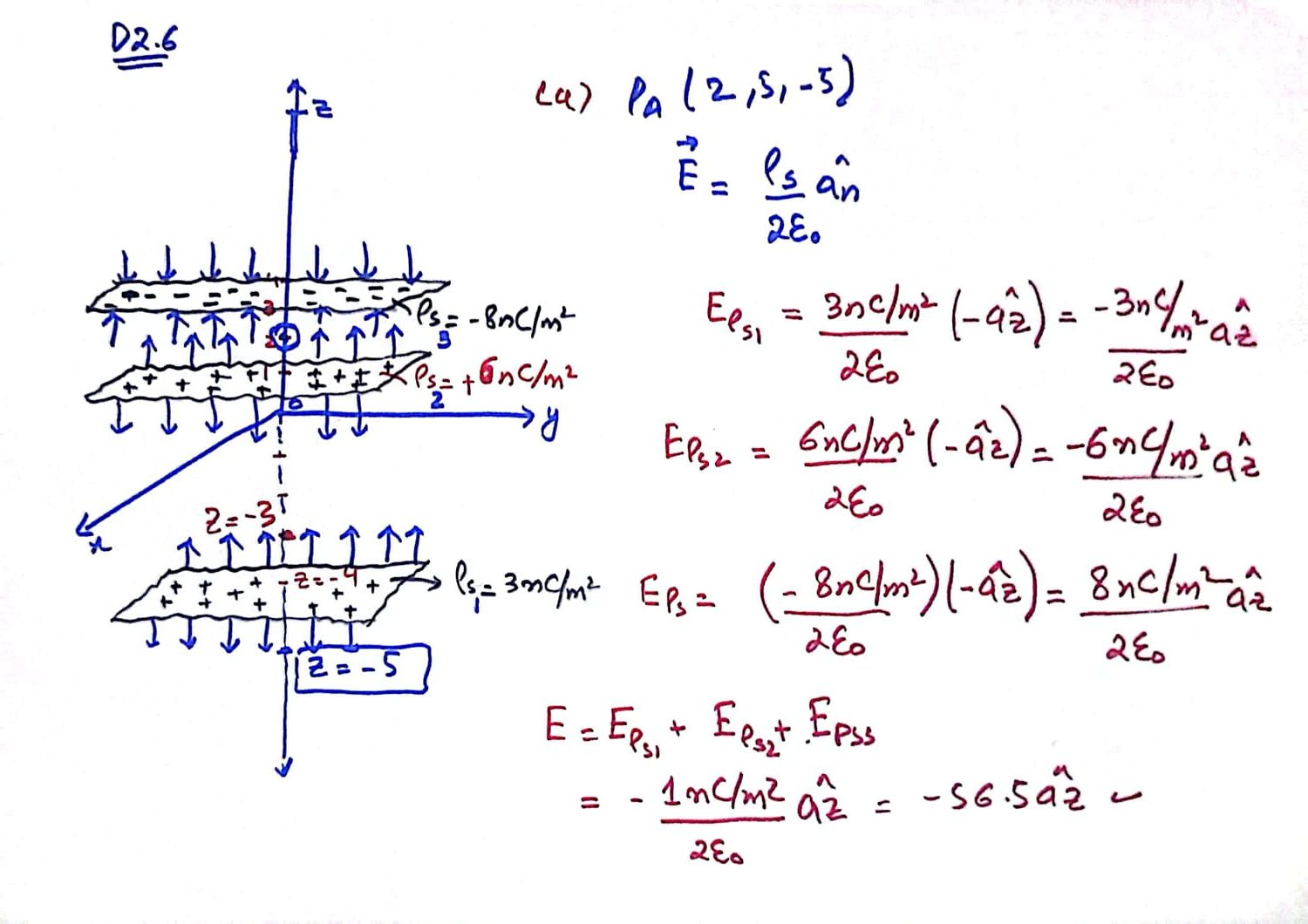
Also read here: