Introduction
In this article you will learn about the orthogonal and orthonormal vectors. Then you will see if the set of vectors are not orthogonal or orthonormal then how we can do that using the Gram Schmidt Procedure.
Orthogonal vectors
The vectors u1,u2,u3,…..,un in Rn are called the orthogonal vectors if the dot product of any of these vectors is equal to zero.
Mathematically,
if ui.uj=0 where i and j are not equal.
Example
Consider the vectors u and v such that u=(sinθ+cosθ) and v=(-COSθ+Sinθ) then u.v=-cosθsinθ+cosθsinθ=0. In this case u and v are orthogonal vectors. Similarly, there are many other examples of orthogonal vectors e.g., w=(1,1), y=(2,-2).
Orthonormal vectors
The vectors u1,u2,u3,…..,un in Rn are said to be orthonormal vectors if they are perpendicular to each other so that their dot product is equal to zero and their magnitude is equal to one.
Mathematically, we can write as:
The standard basis of Rn e1,e2,e3,…..en are actually orthonormal.
As e1=(1,0,0,…….)
e2=(0,1,0,0,……)
e3=(0,0,1,0,……)
.
.
.
.
en=(0,0,0…….1)
It can be noticed that the magnitude of e1,e2,e3,….en=1 and they all are perpendicular to each other.
Example of orthonormal Vectors
In the above example, the vectors u=(sinθ+cosθ) and v=(-COSθ+Sinθ) have magnitude=1. Also their do product is equal to zero so they are orthonormal vectors.
What is the magnitude/norm/length of a vector ?
The magnitude, length or norm are the different names for a same thing. The magnitude actually determines the distance of a vector from the origin. The magnitude of a vector u is denoted by ||u|| and it is equal to:
||u||=u.u (dot product of u vector with itself).
How to test the given vectors are orthogonal or orthonormal?
Here is the video lecture for testing either the given set of vectors represents the orthogonal or orthonormal vectors
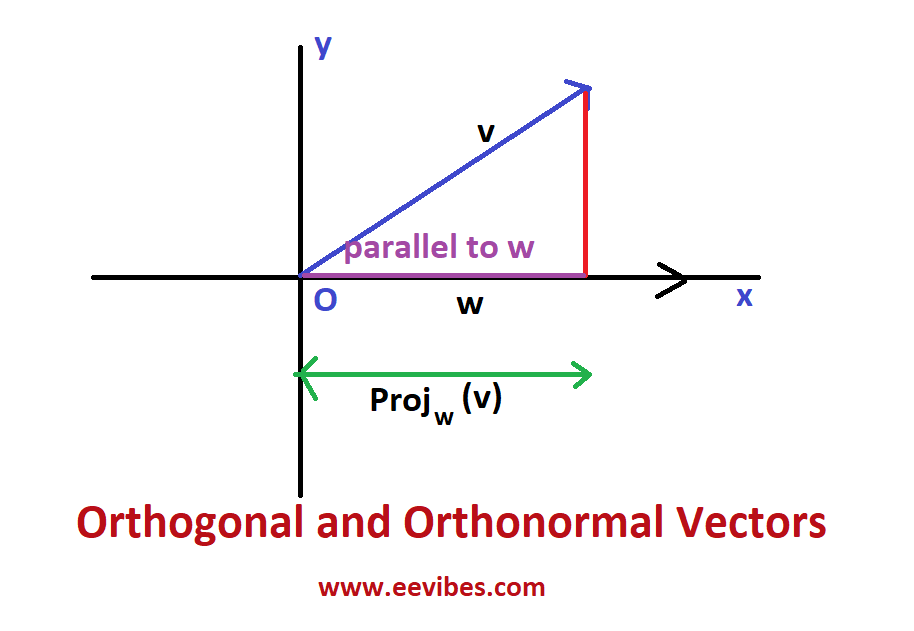
What is the projection of a vector on another vector?
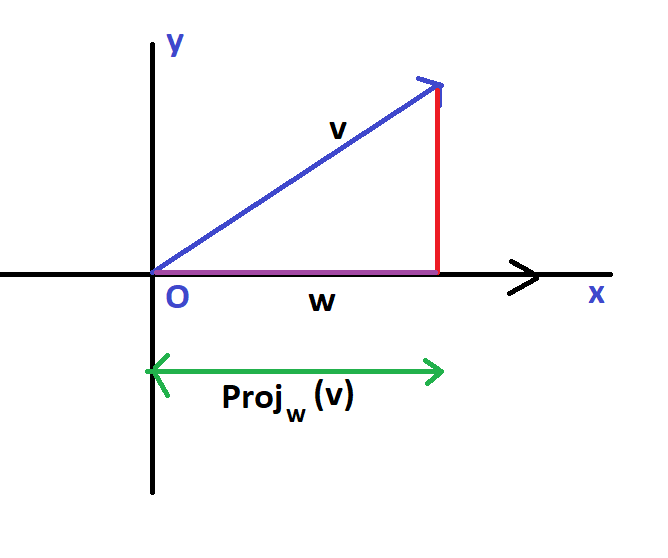
The projection of a vector v on the vector w is found by drawing the perpendicular of v on w as shown below.

So, Projection of vector v on vector w is shown using the purple line. This is called the scalar projection of vector v on w vector. It merely gives us the idea of how long vector v is on vector w. The scalar projection can be found using the property of dot product of two vectors.
Scalar Projection of a vector on another vector
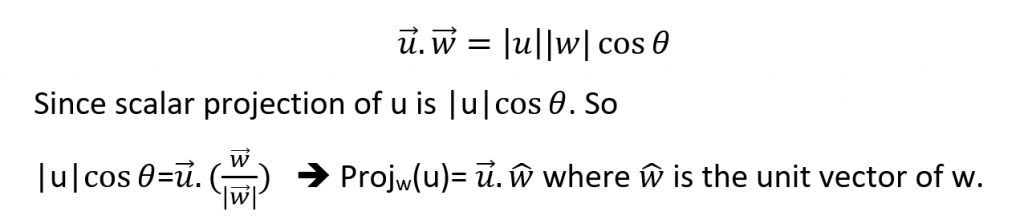
No, for the two vectors u=(1,2) and w=(3,1) the scalar projection of v on w = v. unit vector of w
=(1,2).(3,1)/sqrt(10)
=(3+2)/sqrt(10)
=5/sqrt(10)
In order to convert this scalar projection into vector projection, we need to add just direction to this projection. Since this projection has the same direction as that of w. so we will take dot product with the unit vector of w.
vector projection of v on w = [(3,1)/sqrt(10)][5/sqrt(10)]
=(15,5)/10
=(3/2, 1/2)
so this is the vector projection. It can be noticed that this vector projection is actually parallel to w. This is also called vector projection of v that is parallel to w.
How to find the scalar projection of a vector?
Here is the video lecture of how to find the scalar projection of a vector.
Projection of a vector video lecture
Here is the video link of how to find the vector projection
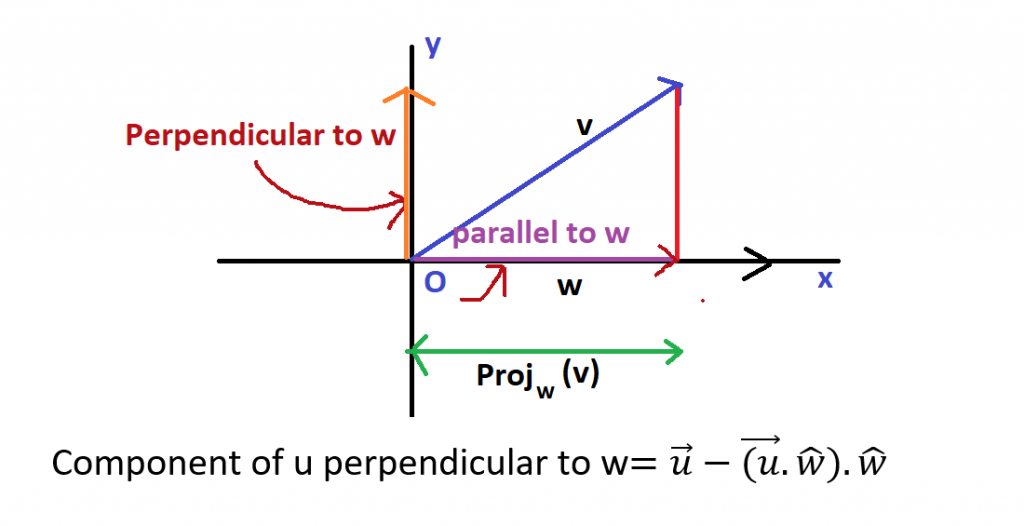
Component of a vector perpendicular to another vector
So far you have found how to determine the projection of a vector v that is parallel to the other vector w. Now lets just expand this concept. As we know that any vector can be represented as a summation of its two components (x and y).
Or
A=Ax+Ay
where
Ax= |A|cosθ
Ay=|A|sinθ
Simply if we subtract a parallel component of a vector from it, then we are left with only perpendicular component just like shown below
What is the Gram Schmidt Procedure?
The Gram Schmidt procedure is used for the set of vectors that are not orthogonal/ orthonormal. This Procedure will make them orthogonal/orthonormal using the above mentioned procedure.
So, let us assume that we have a set of vectors (v1,v2,v3,v4) and we want to orthogonalize/orthonormalize them.
Orthogonalizing the vectors
One of these vectors is selected as it is ……call it v1
v1=u1
u2=v2- (v2.u1).(u1)
v3’= v3-(v3.u1)(u1)-(v3.u2)(u2)
So in general we can write as:

Example of Gram Schmidt Procedure

What is the Gram Schmidt Procedure?
Here is the video lecture for Gram Schmidt Procedure
Also read here