Introduction to scalar and Vector quantities
what are the examples of scalar and vector quantities? All the physical quantities in our surroundings can be classified either as scalar or vector. For example the speed of light is a scalar quantity. The air pressure in a room, mass of a body, temperature at any point in a cup of tea are also a scalar quantities. Basically a scalar quantity is one which needs only magnitude for its complete description while a vector needs both magnitude and direction for its representation. The gravitational force is a vector quantity as it acts always downward and has a specific value. Other examples of vector quantities are: velocity of sound in air, flow of fluid, a straight line from positive to negative terminal of a storage battery.
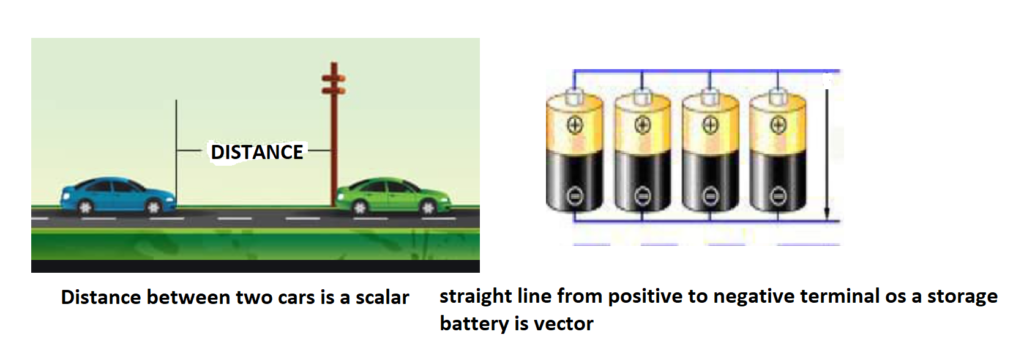
Representation of a scalar and vector
Mathematical Representation
Mathematically a scalar quantity only needs a real number for example x,y,and z are the letters that can be used for representation of any scalar. While the vectors quantities are represented in specific dimensions usually a 2D, 3D or nD.
Lets say A is some vector quantity then mathematically it is written as:
![]()
where A hat is the unit vector of A and |A| represents the magnitude of A.
Graphical Representation
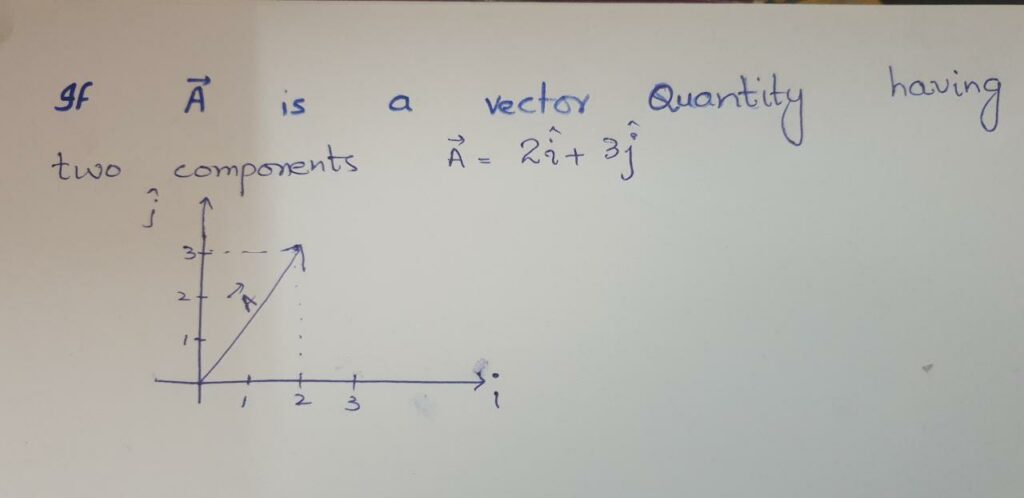
Vectors Algebra
All algebraic operations except (division) can be performed on vector quantities. For performing additions of any vectors it is needed to add their corresponding elements.
Addition
S0, if
![]()
Parallelogram Law is followed for any number of vectors. If we need to add multiple vectors graphically, then it is necessary to add one by one using head to tail rule.
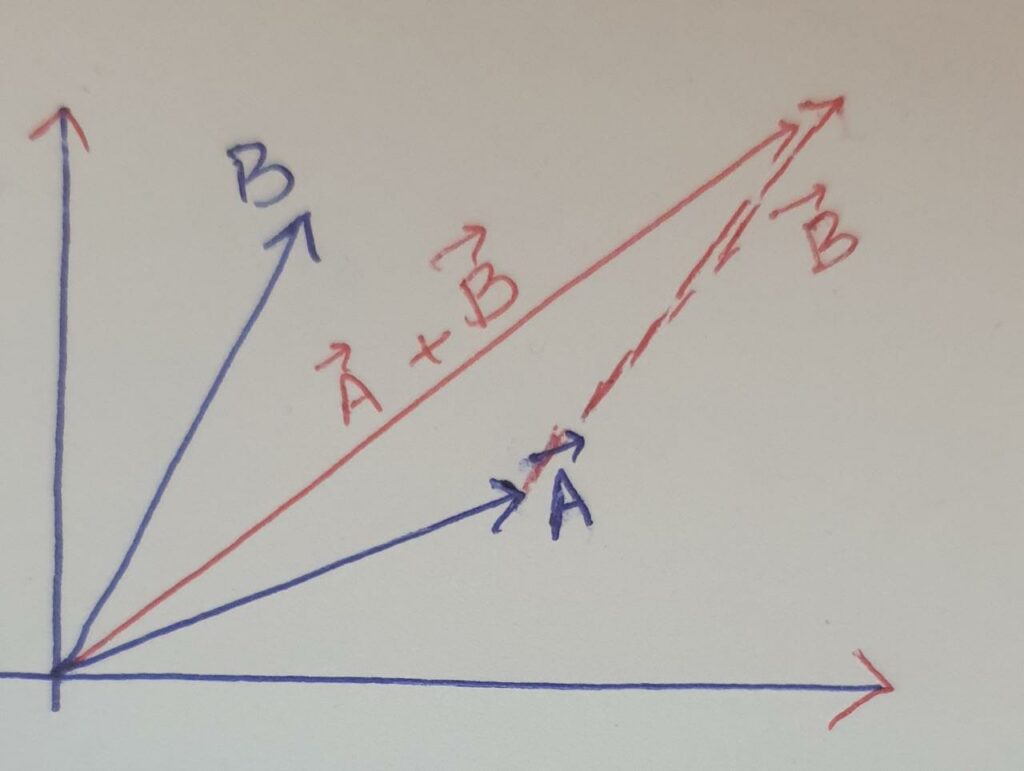
The above figure shows the summation of two vectors using head to tail rule. If two vectors need to be added then they must first join with each other such that the head of one vector combines with the tail of other. For this we draw a parallel vector of one vector as shown for vector B. then after drawing so, the head of one vector is joined with the tail of the second. Hence the resultant vector A+B is formed.
Subtraction
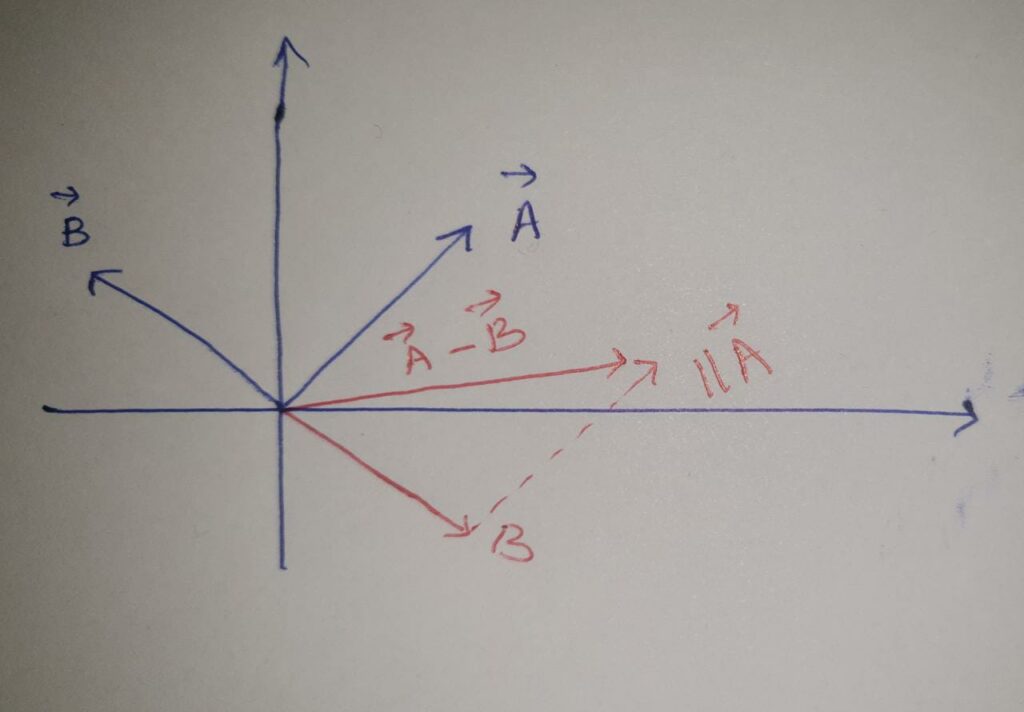
For performing the subtraction of two vectors the same head to tail rule is followed. The only difference is to invert the direction of a vector we want to subtract. So if A-B is to be performed then invert the direction of B and then add it int0 A. so A-B=A+(-B).
Multiplication of two vectors
The multiplication of vectors can result either a scalar quantity or a vector quantity. When the result is a scalar quantity it is called scalar or dot product and when the resultant is a vector quantity it is called a vector or cross product. So i hope the answer is given what are the scaler and vector quantities?
Watch here for more detail:
https://www.youtube.com/watch?v=GmOKt-6SgsA
Also watch:
Also read here :
https://eevibes.com/what-are-the-vector-spaces/
what is the vector space in linear algebra? vector space example