How to find the basis of a vector space?

How to find the basis of a vector space V? In order to find the basis of a vector space , we need to check two properties:

1. The vectors should be linearly independent.
2. These vectors should span in that vector space.

If both of these properties hold, then it means the given set of vectors form the basis otherwise not.

What are the standard basis of R²?

The standard basis of R² is composed of two vectors v1(1,0) and v2=(0,1). The reason is, these two vectors can be used for generating any vector having two components. These two vectors are actually the axes : x-axis and y-axis. The first component of v1 indicates the presence of x axis while y-axis is missing. Similarly in v2, the second component=1 indicating the presence of y axis and all x-component along it is equal to zero.

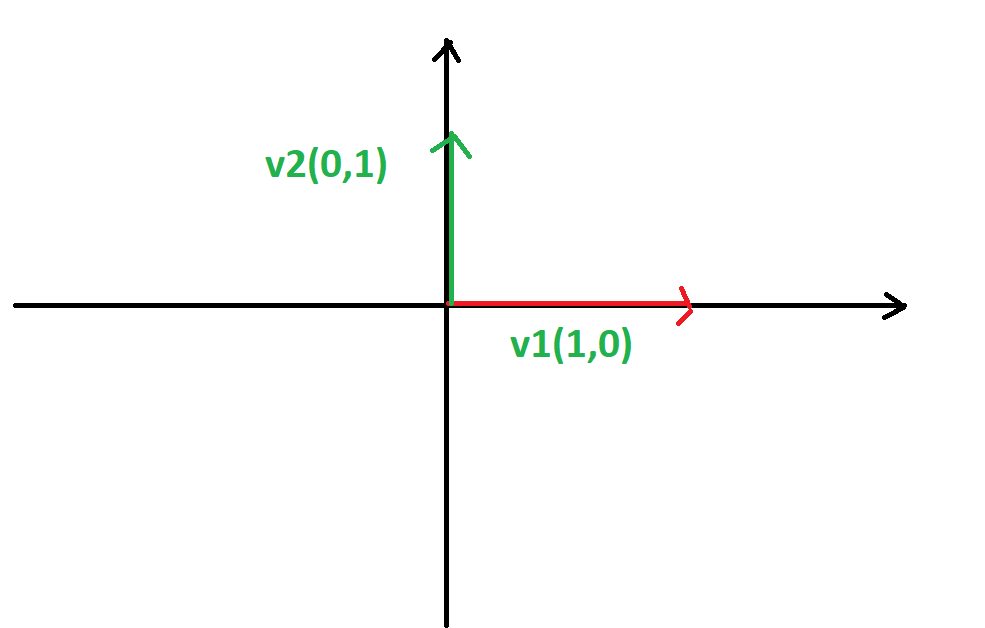
Lets say we want to see first property i.e., v1 and v2 are linearly independent or not. For this solve

c1v1+c2v2=0

c1(1,0)+c2(0,1)=(0,0)

It can be seen easily only c1=0 and c2=0. No other values of c1 and c2 satisfy the above equation. That is why v1 and v2 are linearly independent.

Now, check either they span the vector space R² or not?

For this we will try to generate any vector having components (a1,a2) using the linear combinations of these two vectors.

(a1,a2)=c1v1+c2v2

Lets say

a1=5, a2=6 so we will have

(5,6)=c1v1+c2v2

(5,6)=c1(1,0)+c2(0,1)

1.c1+0.c2=5

0.c1+1.c2=6

By solving these equations, we will get c1=5 while c2=6

As

(5,6)=5(1,0)+6(0.1)

So, it is clear that we can generate any vector in R² using these vectors. So v1 and v2 span the vector space V.

From the above explanation both properties of the basis are satisfied, that is why v1 and v2 form the basis in R²

The vectors e1=(1,0) and e2=(0,1) are called the standard basis of R². Similarly, the vectors e1=(1,0,0), e2=(0,1,0), and e3=(0,0,1) are said to form the standard basis of R³.

This is because of the fact that you can generate any vector having three components using these vectors. For example if we want to generate the vector A=(2,3,-1) as a linear combination of e1,e2,e3.

so,

A=c1e1+c2e2+c3e3

(2,3,-1)=2.(1,0,0)+3(0,1,0)-1(0,0,1)

where c1=2, c2=3, c3=-1

Hence we can write the standard basis of Rⁿ as:

e1=(1,0,0,……..0), e2=(0,1,0,0,…….0), e3=(0,0,1,0,…..0), en=(0,0,0,……..0,1)

Also watch this lecture for more details.

Basis and Dimension of a Vector Space

 

Find the Dimensions of Solution Space of the given matrix

 

what is the vector space in linear algebra? vector space example