Table of Contents

What is the Vector Algebra?

what is the vector algebra? vector algebra is the first part of vector analysis where we perform basic algebraic operations on vectors that are :

addition
subtraction and
multiplication.

How to add two vectors?

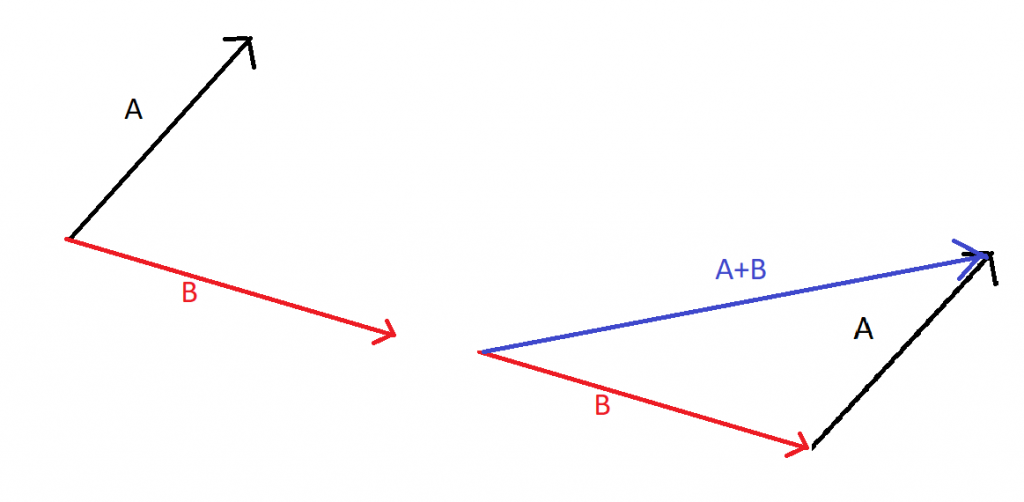
In order to add two or more vectors, we follow the head to tail rule that is implemented using parallelogram rule. If we want to add any two vectors A and B then it is necessary to join the head of one vector with the tail of another vector and after joining them together, the tail of one vector is joined to the head of another vector as shown below.

How to subtract two vectors?

The vectors subtraction can be performed just like the vectors addition. Because if you want to perform the operation A-B then it can also be written as A+(-B)=A-B. While performing the vectors subtraction you just need to invert the sign of the vector that is being subtracted and then add it into the first vector. Consider the following example.

Here it can been that two vectors A and B are subtracted. Fist step is to draw the negative of B that will be in opposite direction to B. Then draw a parallel vector of A on -B. Finally they are added using head to tail rule.

What is the vector multiplication?

There are three types of vector multiplication that are

simple multiplication
scalar or dot product
vector or cross product

simple product

In simple product, a vector is multiplied with a constant K which extends its magnitude and results in a new vector B. So, B=kA. If k is positive then the direction of B is same as that of A and if it is negative, then the direction of B is opposite to that of A.

scalar or dot product

If two vectors are multiplied such that the resultant is a scalar quantity or a number then it is called scalar or dot product. The scalar product of two vectors A and B is written as

A.B=ABCOSʘ

scalar product helps to determine the projection of one vector in the direction of another vector. So the scalar projection of vector A on B is given as

ACOSʘ=A.Ḃ

where Ḃ is the unit vector of vector B.

In order to convert this scalar projection into the vector projection you need to multiply it with unit vector of B again as shown below

ACOSʘ=A.Ḃ.Ḃ

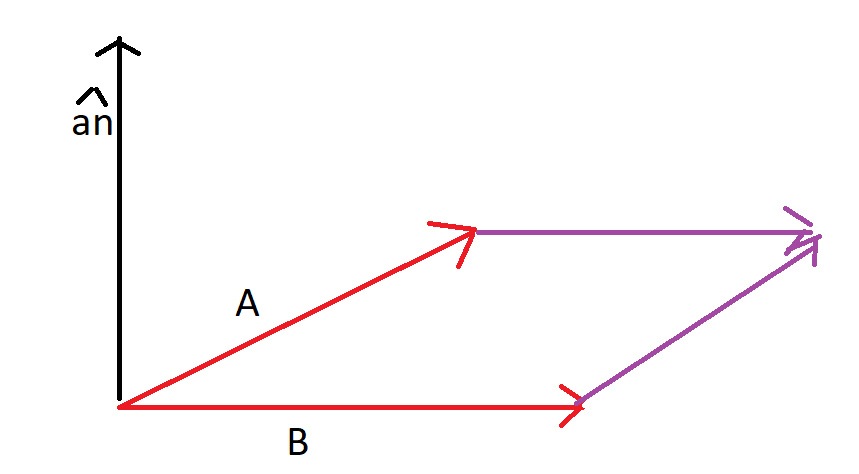
vector or cross product

If the multiplication of two vectors results in a vectors result in a vector quantity then it is called vector or cross product. The formula for cross multiplication of A and B is given as

AxB=ABSinʘ.an

where an is the unit vector perpendicular to the plane containing A and B.