Vector Multiplication

Vector multiplication refers to the ways in which two vectors can be multiplied, and in vector algebra, there are mainly two types of vector multiplication:

Scalar or Dot Product
Vector or Cross Product

Both operations are fundamentals but they produce different kind of results. One gives a scalar as resultant after multiplying the vector quantities, and the other gives a vector.

Scalar or Dot(.) Product of Two Vectors

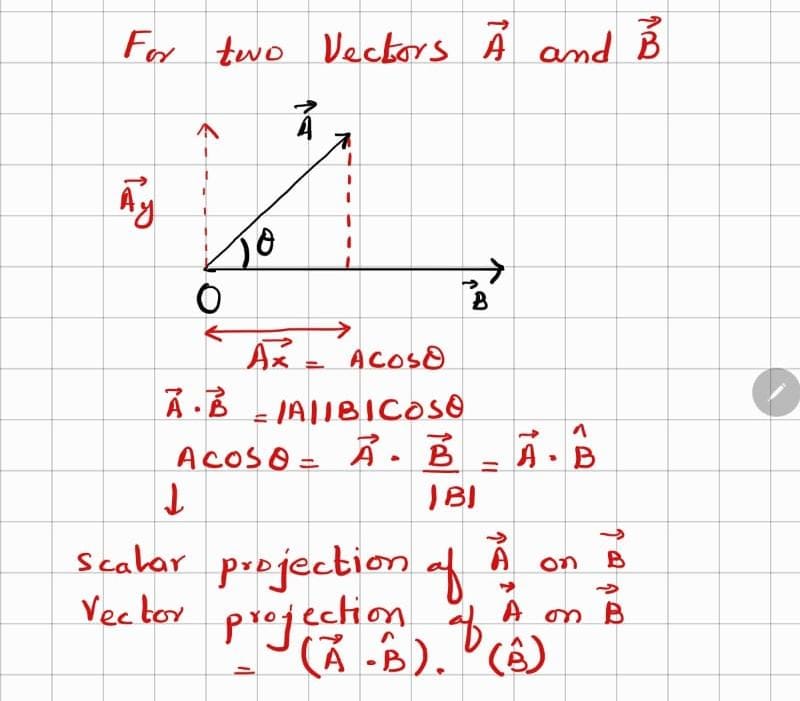
The scalar or dot product of two vectors is defined as:

A⋅B=∣A∣∣B∣cosθ

where $|A|$ and $|B|$ are the magnitudes of the vectors and $\theta$ is the angle between them. In component form, if $A = (a_1, a_2, a_3)$ and $B = (b_1, b_2, b_3)$ then

$A \cdot B = a_1b_1 + a_2b_2 + a_3b_3.$

It is also known as the inner product. The dot product is widely used to calculate work done (force multiplied by displacement in the direction of force). We can also use it to find the angle between vectors. It is also used to determine whether two vectors are perpendicular (since their dot product is zero in that case).

Projection of a vector on another vector

Properties of Scalar or Dot Product

The scalar product (also called the dot product) has several important properties that make it useful in mathematics, physics, and engineering. Here are the main properties explained in paragraph form:

Commutative Property:

The scalar product is commutative, meaning the order of multiplication does not matter. For any two vectors A and B,

$A \cdot B = B \cdot A$

since $\cos\theta = \cos(-\theta)$ . This ensures that the result remains the same regardless of the order in which the vectors are multiplied.

Distributive Property Over Addition:

It is also distributive over vector addition, which means that if we have three vectors A, B, and C, then

$A \cdot (B + C) = A \cdot B + A \cdot C.$ $This property allows us to expand and simplify expressions involving dot products just like algebraic multiplication.$

Another property is that the scalar product of a vector with itself gives the square of its magnitude:

$A \cdot A = |A|^2.$

This makes the dot product useful in defining vector lengths and in finding unit vectors.

Orthogonality:

The scalar product also has the property of orthogonality: if two vectors are perpendicular (at $90^\circ$ $9 0^{\circ}$ ), then

$A \cdot B = 0.$

This condition is often used in geometry and physics to test whether two directions are at right angles.

Finally, the scalar product is not associative with respect to three vectors. For example, $(A \cdot B) \cdot C$ does not make sense because $A \cdot B$ is already a scalar, and a scalar cannot be dotted with another vector. However, it is associative in combination with scalar multiplication, i.e., $(kA) \cdot B = k(A \cdot B)$ , where $k$ is a scalar.

Example of Scalar Product of Two Vectors

Find the scalar product of
\[
\mathbf{A} = (2, -1, 3), \quad \mathbf{B} = (4, 0, -2).
\]The scalar (dot) product is defined as:

\[
\mathbf{A} \cdot \mathbf{B} = a_1b_1 + a_2b_2 + a_3b_3
\]
Substituting the values:
\[
\mathbf{A} \cdot \mathbf{B} = (2)(4) + (-1)(0) + (3)(-2)
\]

Simplify each term:
\[
\mathbf{A} \cdot \mathbf{B} = 8 + 0 – 6
\]

\[
\mathbf{A} \cdot \mathbf{B} = 2
\]

The scalar product is
\[
\mathbf{A} \cdot \mathbf{B} = 2
\]

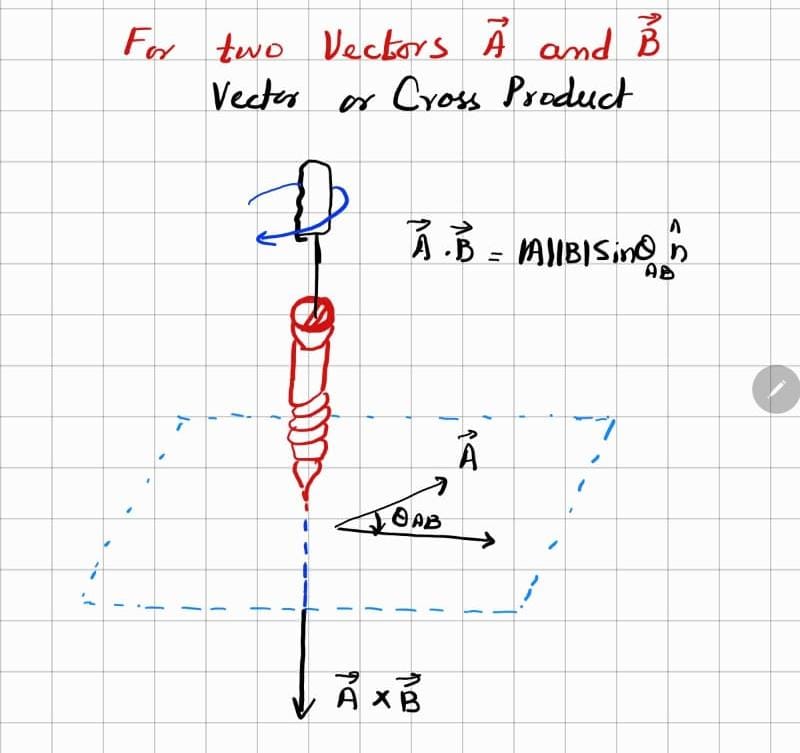
Vector or Cross(X) Product of Two Vectors

The cross product, on the other hand, is a vector quantity and is denoted by $A \times B$ . Its magnitude is given by:

$\times B| = |A||B|\sin\theta$

and the resulting vector is perpendicular to both $A$ and $B$ , with its direction determined by the right-hand rule. In component form, the cross product is expressed using a determinant and gives a new vector. This type of multiplication is useful for finding torque, angular momentum, and the area of parallelograms or triangles formed by two vectors.

Properties of Vector or Cross Product

The cross product (also called the vector product) has several important properties that distinguish it from the scalar (dot) product. These properties make it very useful in physics and engineering for describing rotational effects, torque, and directional relationships. Here are the main properties explained in paragraphs:

The cross product is anti-commutative, which means that reversing the order of the vectors changes the sign of the result. For any two vectors A and B:

$A \times B = – (B \times A).$

This property arises because the direction of the resulting vector depends on the right-hand rule.

It is also distributive over addition. If A, B, and C are vectors, then:

$A \times (B + C) = A \times B + A \times C.$

This allows expansion and simplification of expressions involving cross products in the same way as ordinary multiplication distributes over addition.

Another property is that the cross product of a vector with itself is always zero:

This allows expansion and simplification of expressions involving cross products in the same way as ordinary multiplication distributes over addition.

Another property is that the cross product of a vector with itself is always zero:

$A \times A = 0,$

because the angle between the same vector is $0^\circ$ and $\sin 0 = 0$ .

The cross product is also linked to magnitude and perpendicularity. The magnitude of $A \times B$ is:

$|A \times B| = |A||B|\sin\theta,$

where $\theta$ $θ$ is the angle between the vectors. This means the cross product is maximum when the vectors are perpendicular ( $\theta = 90^\circ$ $θ = 9 0^{\circ}$ ), and zero when they are parallel.

Additionally, the cross product is not associative. In other words:

$(A \times B) \times C \neq A \times (B \times C).$ $(A \times B) \times C \neq = A \times (B \times C) .$

This is an important distinction compared to scalar multiplication. However, it is associative with scalar multiplication, meaning:

$k(A \times B) = (kA) \times B = A \times (kB),$ $k (A \times B) = (k A) \times B = A \times (k B),$

where $\theta$ is the angle between the vectors. This means the cross product is maximum when the vectors are perpendicular ( $\theta = 90^\circ$ ), and zero when they are parallel.

Additionally, the cross product is not associative. In other words:

$(A \times B) \times C \neq A \times (B \times C) .$

This is an important distinction compared to scalar multiplication. However, it is associative with scalar multiplication, meaning:

$k(A \times B) = (kA) \times B = A \times (kB),$

where $k$ $k$ is a scalar.

Finally, the cross product is always perpendicular to both vectors. If $A \times B = C$ $A \times B = C$ , then $C$ $C$ is orthogonal to both $A$ $A$ and $B$ $B$ . This property makes the cross product extremely useful in defining normal vectors to surfaces and in calculating torque and angular momentum in physics.

where $k$ is a scalar.

Example of Vector Product of Two Vectors

Compute the vector (cross) product of
\[
\mathbf{A}=(2,\,-1,\,3), \qquad \mathbf{B}=(4,\,0,\,-2).
\]

By definition,
\[
\mathbf{A}\times\mathbf{B}=
\begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k}\\
2 & -1 & 3\\
4 & 0 & -2
\end{vmatrix}.
\]
Expanding the determinant,
\[
\mathbf{A}\times\mathbf{B}
= \big((-1)(-2)-3\cdot 0\big)\,\mathbf{i}
– \big(2(-2)-3\cdot 4\big)\,\mathbf{j}
+ \big(2\cdot 0-(-1)\cdot 4\big)\,\mathbf{k}.
\]
Simplify each component:
\[
\mathbf{A}\times\mathbf{B}=(2)\,\mathbf{i}-(-4-12)\,\mathbf{j}+(0+4)\,\mathbf{k}
= 2\,\mathbf{i}+16\,\mathbf{j}+4\,\mathbf{k}.
\]
Hence,
\[
\boxed{\;\mathbf{A}\times\mathbf{B}=(2,\,16,\,4)\;}
\]

Vector Triple Product

The vector triple product involves the cross product of a vector with the cross product of two other vectors. It is written as

$\mathbf{A} \times (\mathbf{B} \times \mathbf{C})$

and is different from the scalar triple product $(\mathbf{A} \cdot (\mathbf{B} \times \mathbf{C}))$ .

What is the BAC-CAB Rule?

Formula (BAC–CAB rule)

The vector triple product expands as:

$A \times (B \times C) = (A \cdot C) B - (A \cdot B) C .$

This is known as the BAC–CAB identity. Notice that the result is a linear combination of $\mathbf{B}$ and $\mathbf{C}$ , meaning it lies in the plane spanned by $\mathbf{B}$ and $\mathbf{C}$ . Importantly, the result is never perpendicular to both $\mathbf{B}$ and $\mathbf{C}$ , unlike a simple cross product.

\textbf{Example:} Let
\[
\mathbf{A} = (1,2,3), \quad \mathbf{B} = (2,0,1), \quad \mathbf{C} = (1,-1,2).
\]
Find $\mathbf{A} \times (\mathbf{B} \times \mathbf{C})$.

Using the vector triple product identity:
\[
\mathbf{A} \times (\mathbf{B} \times \mathbf{C}) = (\mathbf{A} \cdot \mathbf{C})\mathbf{B} – (\mathbf{A} \cdot \mathbf{B})\mathbf{C}.
\]

Step 1: Compute dot products.
\[
\mathbf{A} \cdot \mathbf{C} = (1)(1) + (2)(-1) + (3)(2) = 1 – 2 + 6 = 5,
\]
\[
\mathbf{A} \cdot \mathbf{B} = (1)(2) + (2)(0) + (3)(1) = 2 + 0 + 3 = 5.
\]

Step 2: Substitute into formula.
\[
\mathbf{A} \times (\mathbf{B} \times \mathbf{C}) = (5)\mathbf{B} – (5)\mathbf{C}.
\]

Step 3: Expand.
\[
= 5(2,0,1) – 5(1,-1,2)
\]
\[
= (10,0,5) – (5,-5,10).
\]

Step 4: Subtract.
\[
\mathbf{A} \times (\mathbf{B} \times \mathbf{C}) = (10-5, 0-(-5), 5-10) = (5,5,-5).
\]\[
\mathbf{A} \times (\mathbf{B} \times \mathbf{C}) = (5,\,5,\,-5).
\]

Thus, vector multiplication is not a single operation but rather a set of methods that extend the idea of multiplication to vectors, providing tools for solving a wide range of problems in physics, engineering, and geometry. The dot product emphasizes projection and magnitude in a particular direction, while the cross product emphasizes orientation and perpendicularity in space. Together, they form the backbone of many vector-based calculations.

Vector Multiplication: Scalar or Dot Product, Vector or Cross Product