Introduction

Game theory is a mathematical framework for analyzing strategic interactions among rational decision-makers. It studies how individuals or entities make choices that depend on the actions of others, aiming to predict outcomes in situations of conflict or cooperation. Here’s a concise overview based on your request:

Basic Elements in Game Theory

Players: Decision-makers (individuals, firms, countries, etc.).
Strategies: Possible actions or plans players can choose.
Payoffs: Outcomes (rewards or costs) resulting from chosen strategies, often represented numerically.
Games: Structured scenarios defined by players, strategies, payoffs, and rules.
Equilibrium: A state where no player can improve their payoff by unilaterally changing their strategy (e.g., Nash Equilibrium).

Types of Games in Game Theory

Cooperative vs. Non-Cooperative Games

Cooperative games involve players who can form binding agreements or coalitions to achieve joint outcomes, focusing on how groups can maximize collective payoffs and how to divide the resulting benefits. For example, in a business merger, firms collaborate to increase profits and negotiate how to share them. Non-cooperative games, by contrast, assume players act independently, each pursuing their own interests without enforceable agreements. The Prisoner’s Dilemma is a classic example, where two suspects decide independently whether to confess, often leading to suboptimal outcomes due to lack of trust. The distinction lies in whether players can commit to coordinated strategies, with cooperative games emphasizing coalition formation and non-cooperative games focusing on individual strategic choices.

Zero-Sum vs. Non-Zero-Sum Games

Zero-sum games are characterized by a fixed total payoff, where one player’s gain is exactly equal to another’s loss. Chess and poker are quintessential examples, as one player’s victory directly results in the other’s defeat. These games model pure competition. Non-zero-sum games, however, allow for outcomes where the total payoff can increase or decrease, enabling mutual benefit or mutual loss. For instance, in trade negotiations, both parties can gain from cooperation (e.g., lower tariffs) or lose from conflict (e.g., trade wars). Non-zero-sum games reflect real-world scenarios where collaboration can create value, unlike the strictly competitive nature of zero-sum games.

Simultaneous vs. Sequential Games

In simultaneous games, players make decisions at the same time, without knowledge of others’ choices. Rock-paper-scissors is a clear example, where each player chooses independently, and outcomes depend on the combination of choices. These games often rely on predicting opponents’ strategies. Sequential games, conversely, involve players taking turns, with later players observing prior moves. Chess exemplifies this, as each move informs the next. Sequential games often use backward induction to find optimal strategies, while simultaneous games may require mixed strategies to handle uncertainty, making the timing of decisions a critical factor.

Symmetric vs. Asymmetric Games

Symmetric games feature identical strategies and payoffs for all players, meaning no player has a unique role or advantage. Matching pennies, where both players choose heads or tails with identical payoffs, is a symmetric game. Asymmetric games, however, involve players with different strategies or payoffs, reflecting distinct roles or resources. For example, in a market entry game, an incumbent firm and a new entrant face different costs and benefits. Symmetry simplifies analysis, as players are interchangeable, while asymmetry introduces complexity due to differing incentives and strategic options.

Perfect vs. Imperfect Information Games

Perfect information games provide all players with complete knowledge of the game’s history, including all prior moves. Checkers is an example, as both players see the board’s full state before acting. These games allow precise strategic planning. Imperfect information games, however, involve hidden information, such as opponents’ choices or private data. Poker, where players conceal their cards, exemplifies this, forcing players to rely on probabilities and bluffing. The presence or absence of complete information significantly shape

Classic Examples

Prisoner’s Dilemma

Two criminals are arrested. If they both stay silent, they get light sentences. If one betrays, he goes free and the other gets a heavy sentence. If both betray, both get medium sentences.
Shows why rational people might not cooperate even if it’s in their best interest.

Chicken Game:

Two players head toward a collision. Swerving avoids disaster but looks weak; not swerving risks mutual destruction. Models brinkmanship.

Solution Concepts

Nash Equilibrium: Named after John Nash (played by Russell Crowe in A Beautiful Mind). It’s a stable state where no player can benefit by changing strategy if the others keep theirs unchanged.
Dominant Strategy: A strategy that’s best regardless of others’ actions.
Pareto Efficiency: An outcome where no one can be better off without making someone worse off.
Subgame Perfect Equilibrium: Used in sequential games to ensure strategies are optimal at every stage.

Solved Example: Prisoner’s Dilemma

Problem Setup

Two suspects, Alice and Bob, are arrested and interrogated separately for a crime. They cannot communicate, so they must decide independently whether to Confess or Stay Silent. The payoffs (in years of prison time, where lower is better) depend on their combined choices, as shown in the payoff matrix below:

Alice \ Bob	Stay Silent	Confess
Stay Silent	(-1, -1)	(-10, 0)
Confess	(0, -10)	(-5, -5)

Payoffs: (Alice’s prison time, Bob’s prison time). For example, (-1, -1) means both get 1 year in prison.

Interpretation: If both stay silent, each gets 1 year (light sentence due to lack of evidence). If one confesses and the other stays silent, the confessor goes free (0 years), while the silent one gets 10 years. If both confess, each gets 5 years (reduced sentence for cooperating with police).

Objective

Find the Nash Equilibrium, where no player can improve their payoff by unilaterally changing their strategy, and analyze the outcome.

Step-by-Step Solution

Understand the Strategies:
- Alice’s strategies: Stay Silent or Confess.
- Bob’s strategies: Stay Silent or Confess.
Analyze Alice’s Best Response:
- If Bob Stays Silent:
  - Alice chooses Stay Silent: Payoff = -1 (1 year in prison).
  - Alice chooses Confess: Payoff = 0 (no prison time).
  - Best choice: Confess (0 > -1).
- If Bob Confesses:
  - Alice chooses Stay Silent: Payoff = -10 (10 years in prison).
  - Alice chooses Confess: Payoff = -5 (5 years in prison).
  - Best choice: Confess (-5 > -10).
- Conclusion: Confess is Alice’s dominant strategy (best regardless of Bob’s choice).
Analyze Bob’s Best Response:
- Since the game is symmetric, Bob’s payoffs mirror Alice’s.
- If Alice Stays Silent:
  - Bob chooses Stay Silent: Payoff = -1.
  - Bob chooses Confess: Payoff = 0.
  - Best choice: Confess.
- If Alice Confesses:
  - Bob chooses Stay Silent: Payoff = -10.
  - Bob chooses Confess: Payoff = -5.
  - Best choice: Confess.
- Conclusion: Confess is Bob’s dominant strategy.
Find the Nash Equilibrium:
- A Nash Equilibrium occurs when neither player can improve their payoff by changing their strategy unilaterally.
- Check the (Confess, Confess) outcome:
  - Payoff: (-5, -5).
  - If Alice switches to Stay Silent (while Bob confesses): Payoff = -10 (worse than -5).
  - If Bob switches to Stay Silent (while Alice confesses): Payoff = -10 (worse than -5).
  - Neither can improve by switching, so (Confess, Confess) is a Nash Equilibrium.
- Check other outcomes:
  - (Stay Silent, Stay Silent): Both get -1, but Alice can switch to Confess (0 > -1), so not stable.
  - (Stay Silent, Confess): Alice gets -10, Bob gets 0. Alice wants to switch to Confess (-5 > -10).
  - (Confess, Stay Silent): Bob gets -10, Alice gets 0. Bob wants to switch to Confess (-5 > -10).
- Result: The only Nash Equilibrium is (Confess, Confess), with payoffs (-5, -5).
Pareto Efficiency:
- The outcome (Stay Silent, Stay Silent) gives (-1, -1), which is better for both (1 year vs. 5 years).
- However, it’s not a Nash Equilibrium because each player is tempted to confess.
- (Confess, Confess) is Pareto inefficient, as both could be better off with cooperation.

Interpretation

Outcome: Both Alice and Bob confess, resulting in 5 years in prison each.
Insight: The Nash Equilibrium (Confess, Confess) is suboptimal compared to mutual cooperation (Stay Silent, Stay Silent). This highlights the tension in non-cooperative games, where individual rationality leads to collective inefficiency due to lack of trust or communication.
Real-World Relevance: This models scenarios like business price wars, arms races, or environmental agreements, where mutual cooperation yields better outcomes, but self-interest drives suboptimal choices.

Visualizing Payoffs

The chart below visualizes Alice’s payoffs (prison years) for each strategy combination in the Prisoner’s Dilemma. The matrix chart shows Bob’s strategies on the x-axis and Alice’s on the y-axis, with cell colors and values indicating Alice’s prison time.

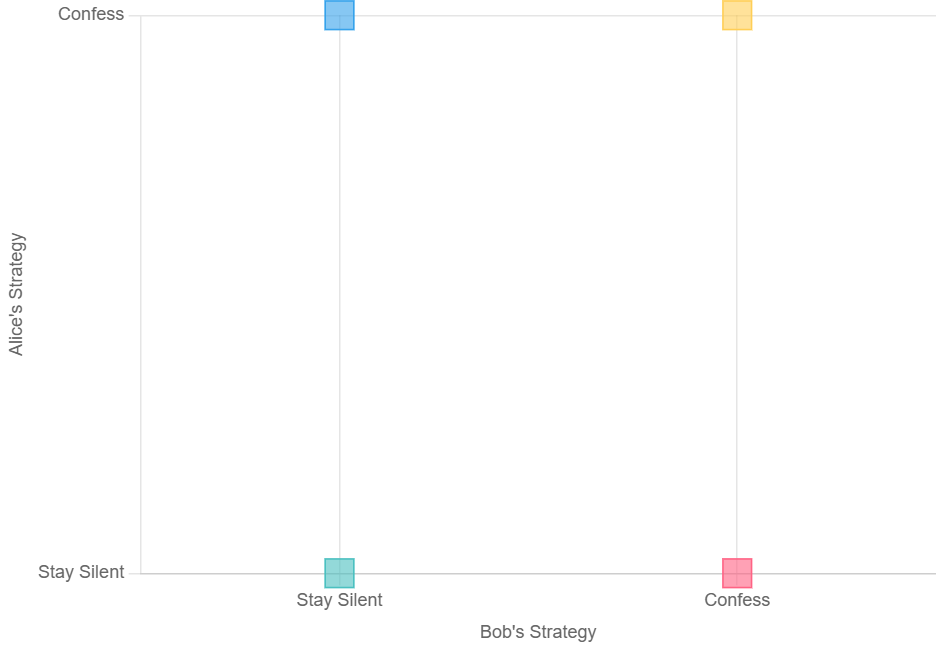
Chart Explanation

Type: Matrix chart, showing a 2×2 grid of Alice’s payoffs.
X-Axis: Bob’s strategies (Stay Silent, Confess).
Y-Axis: Alice’s strategies (Stay Silent, Confess).
Values: Negative numbers represent years in prison (e.g., -1 means 1 year, 0 means no prison time).
Colors: Each cell has a distinct color for clarity:
- (Stay Silent, Stay Silent): -1 (teal).
- (Stay Silent, Confess): -10 (red).
- (Confess, Stay Silent): 0 (blue).
- (Confess, Confess): -5 (yellow).
Purpose: Visualizes how Alice’s payoff varies with her and Bob’s choices, highlighting the Nash Equilibrium (Confess, Confess) at (-5).