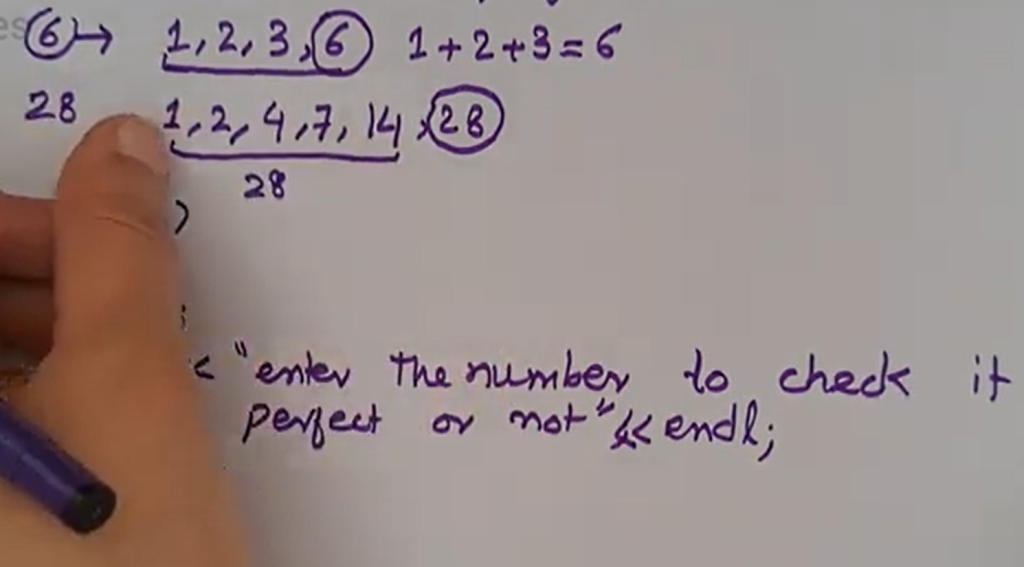
Introduction to Perfect Numbers

Perfect numbers are a special kind of integer in mathematics. A perfect number is a positive integer that is equal to the sum of its proper divisors, excluding itself. In other words, the sum of the positive divisors of a perfect number (excluding the number itself) equals the number itself.

Examples of Perfect Numbers

For example, the first few perfect numbers are:

1. 6: Its proper divisors are 1, 2, and 3, and 1+2+3=61+2+3=6.
2. 28: Its proper divisors are 1, 2, 4, 7, and 14, and 1+2+4+7+14=281+2+4+7+14=28.
3. 496: Its proper divisors are 1, 2, 4, 8, 16, 31, 62, 124, 248, and 1+2+4+8+16+31+62+124+248=4961+2+4+8+16+31+62+124+248=496.
4. 8128: Its proper divisors are 1, 2, 4, 8, 16, 32, 64, 127, 254, 508, 1016, 2032, 4064, and 1+2+4+8+16+32+64+127+254+508+1016+2032+4064=81281+2+4+8+16+32+64+127+254+508+1016+2032+4064=8128.

Perfect numbers have fascinated mathematicians for centuries due to their special properties and connections to various areas of mathematics, such as number theory and algebra. As of now, the largest known perfect numbers are associated with Mersenne primes through the Euclidean formula, but not many perfect numbers are known.

Applications of Perfect Numbers

Perfect numbers have intrigued mathematicians for centuries, and while they don’t have direct practical applications in the same sense as some other mathematical concepts, they do have various connections and implications in different areas of mathematics and beyond. Here are some applications and implications of perfect numbers:

Number Theory:

Perfect numbers are deeply connected to number theory, which is a branch of mathematics that deals with the properties and relationships of numbers. Studying perfect numbers contributes to understanding various number-theoretic concepts such as divisors, factors, and integer sequences.

Euclidean Geometry:

Perfect numbers have been linked to geometric figures in ancient mathematics. For example, the first four perfect numbers correspond to the number of vertices of a tetrahedron, cube, octahedron, and icosahedron inscribed in a sphere, respectively.

Algorithms and Computation:

Perfect numbers have been used in algorithms and computational techniques, particularly in the context of number theory and cryptography. While not directly applicable, the study of perfect numbers has contributed to the development of algorithms for factoring large numbers, which is crucial in cryptography.

https://amzn.to/43B5IxU

Amicable Numbers:

Amicable numbers are pairs of numbers where each number is the sum of the proper divisors of the other. Perfect numbers are closely related to amicable numbers, as the discovery and study of perfect numbers often lead to investigations of amicable numbers.

Recreation and Education:

Perfect numbers serve as interesting topics for recreational mathematics and educational purposes. They can be used to engage students in exploring mathematical concepts such as divisors, factors, and properties of integers.

Historical Significance:

Perfect numbers have historical significance, dating back to ancient Greek mathematicians such as Euclid and Pythagoras. Studying perfect numbers provides insight into the development of mathematical knowledge and the contributions of early mathematicians.

While perfect numbers may not have immediate practical applications in everyday life, their study contributes to a deeper understanding of mathematics and its connections to various other fields. Additionally, the pursuit of knowledge about perfect numbers often leads to discoveries and insights that can have practical applications in areas such as algorithms, cryptography, and computational mathematics.

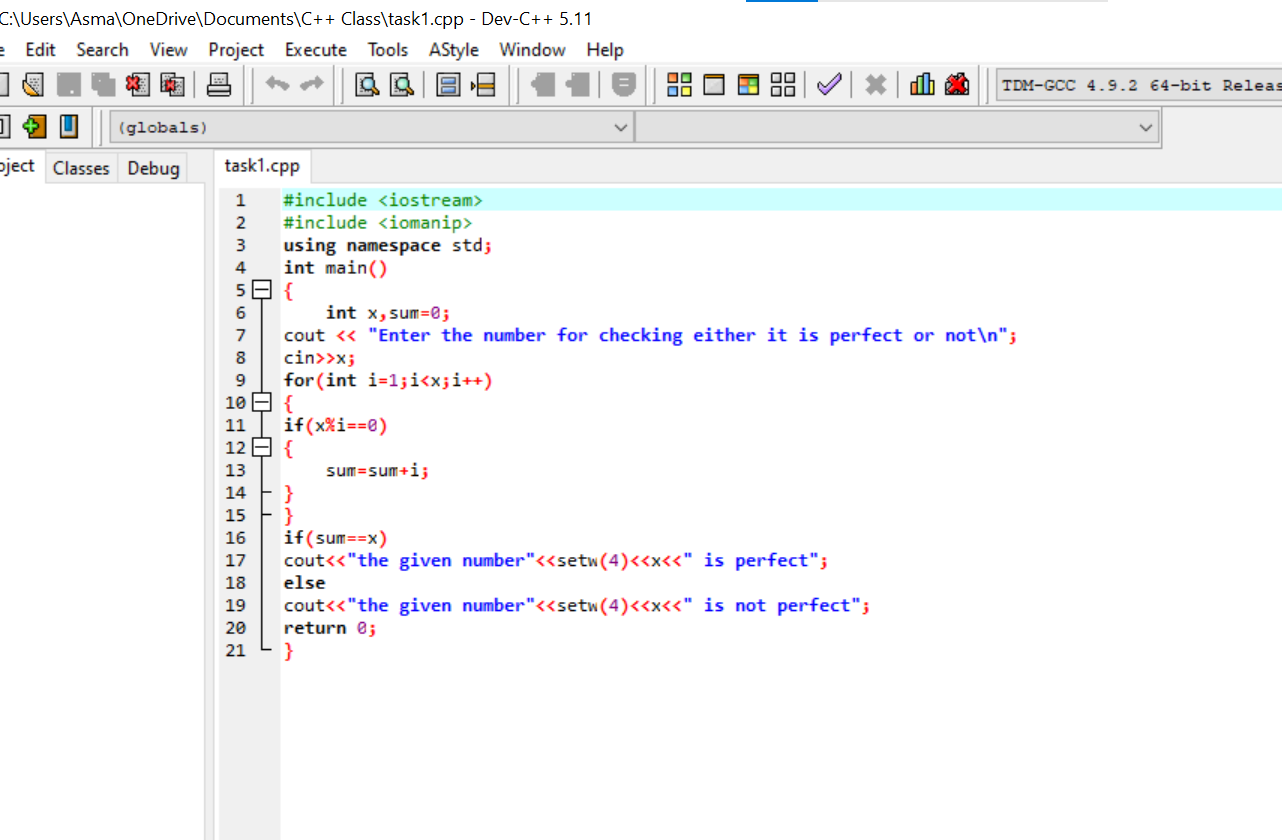
C++ Code for Testing a Number is Perfect or Not?

Here is the program for testing a number is perfect or not?