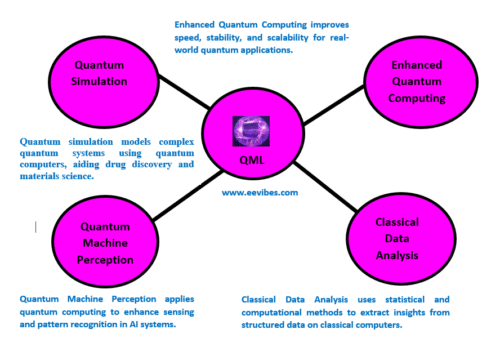
What is Quantum Machine Learning?

Quantum Machine Learning (QML) combines quantum computing with machine learning to potentially solve complex problems faster than classical approaches. It leverages quantum properties like superposition, entanglement, and quantum tunneling to enhance computational efficiency, particularly for tasks involving large datasets or high-dimensional spaces.

The main objective is to exploit the capabilities of quantum systems—such as superposition, entanglement, and quantum parallelism—to enhance the performance of traditional machine learning algorithms.

What are qubits and why are they important in QML?

While classical computers process information in binary bits (0s and 1s), quantum computers use quantum bits or qubits, which can exist in multiple states simultaneously. This allows quantum algorithms to explore multiple solutions at once, potentially reducing the computational time needed to solve complex problems.

In QML, algorithms are designed to run on quantum hardware or simulators, and they typically involve hybrid models, where parts of the learning process are carried out on classical systems and others on quantum systems.

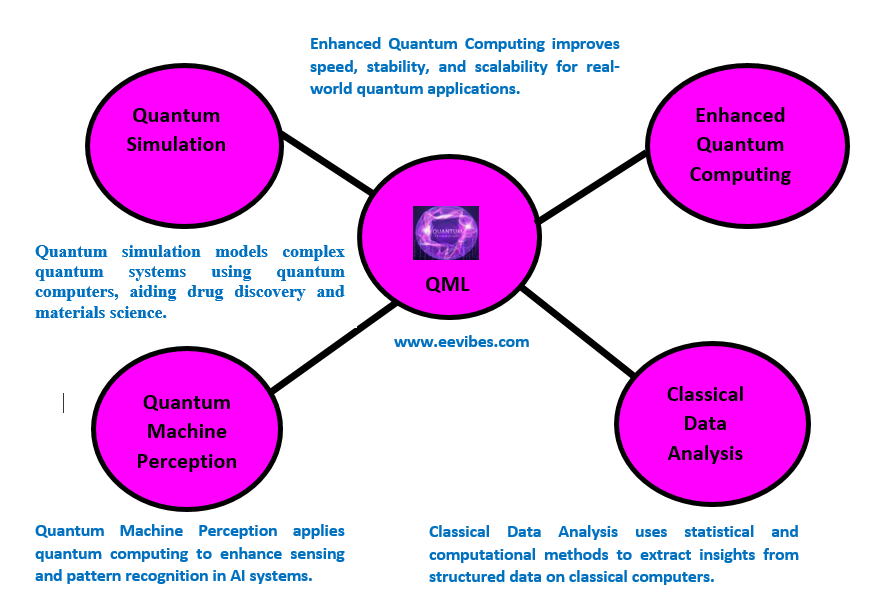
How is QML different from classical machine learning?

QML leverages qubits, which can represent multiple states at once, allowing certain computations (like matrix operations) to be performed exponentially faster than classical methods. This is especially useful for high-dimensional datasets and optimization problems.

Quantum Bits and State

Quantum computing harnesses the principles of quantum mechanics to process and manipulate information in ways that surpass the capabilities of classical computing. At the core of quantum computing are quantum bits, or qubits, which serve as the fundamental units of information.

QUBITS: THE BUILDING BLOCKS OF QUANTUM COMPUTING

In classical computing, the fundamental unit of information is the classical bit, which can exist in one of two states: 0 or 1. Quantum computing, on the other hand, intro- duces qubits as the fundamental units of information. Qubits are quantum systems that can exist in a superposition of both 0 and 1 states simultaneously, allowing for a much richer and more powerful representation of information.

The physical realization of a qubit can vary depending on the underlying technology. For example, qubits can be implemented using trapped ions, superconducting circuits, or quantum dots. Regardless of the physical implementation, qubits must exhibit two key properties: superposition and entanglement.

Superposition

Superposition is a fundamental property of qubits that allows them to exist in a coherent combination of multiple states simultaneously. In other words, a qubit can be in a state that represents both 0 and 1 at the same time, with the specific probabilities of each state determined by the coefficients in its quantum state vector. Mathematically, a qubit in superposition can be represented as:
psi = α[0)+B|1),

where a and ẞ are complex probability amplitudes, and [0) and |1) represent the basis states of the qubit. The coefficients a and ẞ must satisfy the normalization condition |a|^2 + |B|^2 = 1 to ensure that the total probability of measuring the qubit in either state is conserved.
Superposition enables qubits to simultaneously explore multiple computational paths and perform computations in parallel, providing the potential for significant speedup in certain algorithms.

Entanglement

Entanglement is another crucial property of qubits that allows for strong correlations between multiple qubits, even when they are physically separated. When qubits are entangled, their quantum states become interdependent, and the measurement out- come of one qubit can instantaneously influence the state of the other, regardless of the distance between them. This phenomenon, often referred to as “spooky action at a distance,” defies classical intuition but is a fundamental feature of quantum mechanics. Entangled qubits are described by a joint quantum state that cannot be decomposed into individual qubit states. The state of a two-qubit entangled system can be expressed as:
psi=a00) + B01)+y10)+811),

where a, ẞ, y, and 8 are complex probability amplitudes. The entanglement between qubits allows for the representation of highly correlated information and enables quantum algorithms such as quantum teleportation and quantum error correction. Entanglement is a valuable resource in quantum computing as it enables the exploitation of parallelism and enables novel computational capabilities that surpass classical systems.

Quantum Gates and Operations

In classical computing, logic gates form the building blocks of digital circuits and enable the manipulation of classical bits. Similarly, in quantum computing, quantum gates serve as the fundamental operations for manipulating qubits. Quantum gates are unitary operators that transform the quantum state of one or more qubits. The choice and arrangement of quantum gates determine the computational operations performed on the quantum state. These gates can be combined to create quantum circuits that implement specific algorithms or perform desired computations.

Single-Qubit Gates

Single-qubit gates act on individual qubits and allow for the manipulation of their quantum states. Some commonly used single-qubit gates include:
Pauli-X Gate (X gate): The Pauli-X gate is analogous to the classical NOT gate and flips the state of a qubit from |0) to | 1) and vice versa. Mathematically, it can be represented as:

\[
X =
\begin{bmatrix}
0 & 1 \\
1 & 0
\end{bmatrix}
\]

Pauli-Y Gate (Y gate): The Pauli-Y gate is another single-qubit gate that introduces a phase shift between the basis states. It rotates the state of a qubit around the y-axis of the Bloch sphere. Mathematically, it can be rep- resented as:

\[
Y =
\begin{bmatrix}
0 & -i \\
i & 0
\end{bmatrix}
\]
Pauli-Z Gate (Z gate): The Pauli-Z gate applies a phase flip to the qubit state, leaving |0) unchanged and flipping the sign of | 1). Mathematically, it can be represented as:
\[
Z =
\begin{bmatrix}
1 & 0 \\
0 & -1
\end{bmatrix}
\]

Hadamard Gate (H gate): The Hadamard gate is a versatile gate that creates superposition by transforming |0) to an equal superposition of 10) and | 1). It also introduces a phase shift, rotating the state around the x-axis of the Bloch sphere. The Hadamard gate is represented by the following matrix:

\[
H = \frac{1}{\sqrt{2}}
\begin{bmatrix}
1 & 1 \\
1 & -1
\end{bmatrix}
\]

These single-qubit gates can be combined and applied sequentially or in parallel to perform complex operations on a quantum state.

Multi-Qubit Gates

Multi-qubit gates allow for the interaction and entanglement of multiple qubits, enabling the implementation of quantum algorithms. Some commonly used multi- qubit gates include:
Controlled-NOT Gate (CNOT gate): The CNOT gate, also known as the controlled-X gate, is a two-qubit gate that performs an X gate operation on the target qubit (the second qubit) conditioned on the state of the control qubit (the first qubit). It can be represented as:

\[
\text{CNOT} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{bmatrix}
\]

The CNOT gate is crucial for creating entanglement between qubits and performing quantum computations.
• Toffoli Gate (CCNOT gate): The Toffoli gate is a three-qubit gate that acts as a controlled-controlled-NOT gate. It performs an X gate operation on the target qubit (the third qubit) conditioned on the states of the two control qubits (the first and second qubits). It can be represented as:

\[
\text{CCNOT} =
\begin{bmatrix}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 0
\end{bmatrix}
\]

The Toffoli gate is a universal gate, meaning that any quantum computation can be expressed using the combination of Toffoli gate and single-qubit gates.

Controlled-Z Gate (CZ Gate)

The CZ gate applies a Pauli-Z operation to the target qubit only if the control qubit is in the $\ket{1}$ state. It’s used in many quantum algorithms and for generating entanglement.

\[
\text{CZ} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & -1
\end{bmatrix}
\]

SWAP Gate

The SWAP gate exchanges the states of two qubits. It’s used to move quantum data in a quantum circuit without measuring or destroying entanglement.

\[
\text{SWAP} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
\]

Fredkin Gate (Controlled-SWAP or CSWAP)

The Fredkin gate is a 3-qubit gate that swaps the last two qubits only if the first (control) qubit is $\ket{1}$. It’s useful in reversible logic and certain quantum algorithms.

\subsection*{Effect on Basis States}

\[
\text{Fredkin} \ket{a, b, c} =
\begin{cases}
\ket{a, c, b} & \text{if } a = 1 \\
\ket{a, b, c} & \text{if } a = 0
\end{cases}
\]

key challenges in QML

One of the key challenges in QML is the current limitation of quantum hardware—known as the Noisy Intermediate-Scale Quantum (NISQ) era. These devices are prone to errors and have limited qubit numbers. As such, most research is done using simulators or small-scale quantum processors. Nonetheless, QML holds great promise in domains such as optimization, finance, quantum chemistry, and even healthcare, where massive datasets and complex patterns are involved.