Introduction to Hierarchical Clustering

Hierarchical clustering is a method of cluster analysis that builds a hierarchy of clusters. There are two main types of hierarchical clustering: Agglomerative (bottom-up) and Divisive (top-down). In this example, we’ll focus on Agglomerative Hierarchical Clustering, which starts by treating each data point as a single cluster and then iteratively merges the closest pairs of clusters until all data points are in a single cluster.

Example Problem:

Let’s consider the following dataset of 5 points in 2D space:

 

$$\text{Data Points: }A(1,1),B(2,1),C(4,3),D(5,4),E(6,5)$$

Data Points: 

A(1,1),

B(2,1),

C(4,3),

D(5,4),

E(6,5)

We will use Euclidean distance as the distance metric and single linkage (minimum distance between clusters) as the linkage criterion.

Step 1: Compute the Distance Matrix

First, compute the pairwise Euclidean distances between all points. The Euclidean distance between two points

$(x_1,y_1)$

(x1​,y1​) and

$(x_2,y_2)$

(x2​,y2​) is:

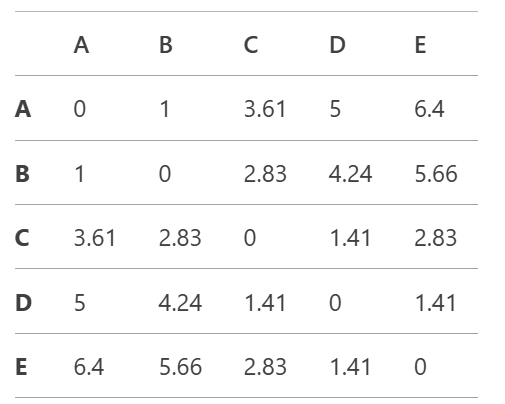
The initial distance matrix is:

Step 2: Merge the Closest Clusters

The smallest distance in the matrix is 1 (between A and B). Merge A and B into a new cluster AB.

Update the distance matrix using single linkage (minimum distance between clusters):

• Distance between AB and C: 
  $\min (d(A,C),d(B,C))=\min (3.61,2.83)=2.83$ 

  $\min (d(A,C),d(B,C))=\min (3.61,2.83)=2.83$

• Distance between AB and D: 
  $\min (d(A,D),d(B,D))=\min (5,4.24)=4.24$ 

  $\min (d(A,D),d(B,D))=\min (5,4.24)=4.24$

• Distance between AB and E: 
  $\min (d(A,E),d(B,E))=\min (6.4,5.66)=5.66$ 

  $\min (d(A,E),d(B,E))=\min (6.4,5.66)=5.66$

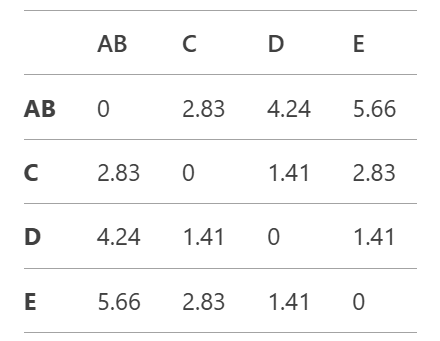
The updated distance matrix is:

 

Step 3: Merge the Next Closest Clusters

The smallest distance in the updated matrix is 1.41 (between C and D). Merge C and D into a new cluster CD.

Update the distance matrix using single linkage:

• Distance between AB and CD: 
  $\min (d(AB,C),d(AB,D))=\min (2.83,4.24)=2.83$ 

  $\min (d(AB,C),d(AB,D))=\min (2.83,4.24)=2.83$

• Distance between CD and E: 
  $\min (d(C,E),d(D,E))=\min (2.83,1.41)=1.41$ 

  $\min (d(C,E),d(D,E))=\min (2.83,1.41)=1.41$

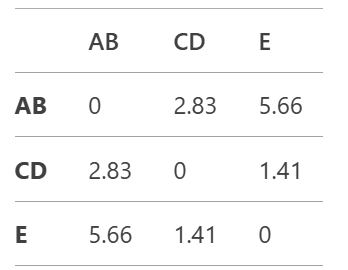
The updated distance matrix is:

Step 4: Merge the Next Closest Clusters

The smallest distance in the updated matrix is 1.41 (between CD and E). Merge CD and E into a new cluster CDE.

Update the distance matrix using single linkage:

• Distance between AB and CDE: 
  $\min (d(AB,CD),d(AB,E))=\min (2.83,5.66)=2.83$ 

  $\min (d(AB,CD),d(AB,E))=\min (2.83,5.66)=2.83$

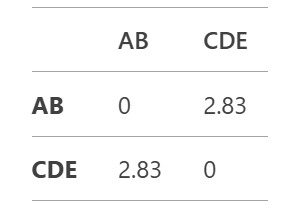
The updated distance matrix is:

Step 5: Merge the Final Clusters

The smallest distance in the updated matrix is 2.83 (between AB and CDE). Merge AB and CDE into a single cluster ABCDE.

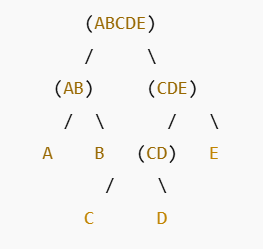
Dendrogram

The hierarchical clustering process can be visualized using a dendrogram:

Final Clusters:

• At a distance threshold of 1, the clusters are: {A, B}, {C}, {D}, {E}
• At a distance threshold of 1.41, the clusters are: {A, B}, {C, D}, {E}
• At a distance threshold of 2.83, the clusters are: {A, B}, {C, D, E}
• At a distance threshold of 5.66, all points are in one cluster: {A, B, C, D, E}