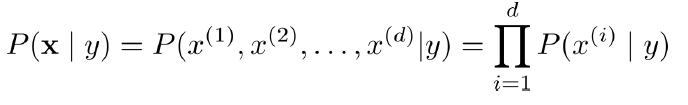
Introduction to Bayes Theorem

The Naive Bayes algorithm is a simple, probabilistic machine learning method used for classification tasks. It’s based on Bayes’ Theorem, which calculates the probability of an event given prior knowledge. The “naive” part comes from its assumption that features (input variables) are independent of each other, which simplifies computations but may not always hold true in real-world data.

Main Idea Behind Naive Bayes Algorithm

The main idea behind Naive Bayes Algorithm is Bayes Theorem which is based on conditional probability and Bayes theorem.

Conditional Probability and Bayes Theorem

Conditional probability, important concept in probabilistic modeling, allows us to update probabilistic models when additional information is revealed.

Probability of even A given the event B:

\begin{equation}
P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}
\end{equation}

Similarly, we have

\begin{equation}
P(B|A) = \frac{P(A|B) \cdot P(B)}{P(A)}
\end{equation}

since P(A∩B)=P(B∩A), we can write P(A∣B).P(B)=P(B∣A).P(A)

P(A|B)=P(B|A).P(A)/P(B​)

Law of Total Probability

Defining the Law of Total Probability formula
\begin{equation}
P(A) = \sum_{i=1}^{n} P(A|B_i) \cdot P(B_i)
\end{equation}

Types of Naive Bayes:

• Gaussian Naive Bayes: Assumes continuous features follow a normal (Gaussian) distribution.
• Multinomial Naive Bayes: Used for discrete data, like word counts in text classification (e.g., spam detection).
• Bernoulli Naive Bayes: Handles binary/Boolean features, often used in document classification.

Naïve Bayes Classifier

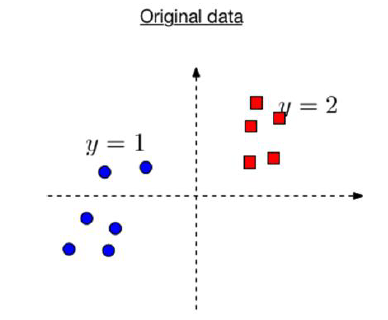
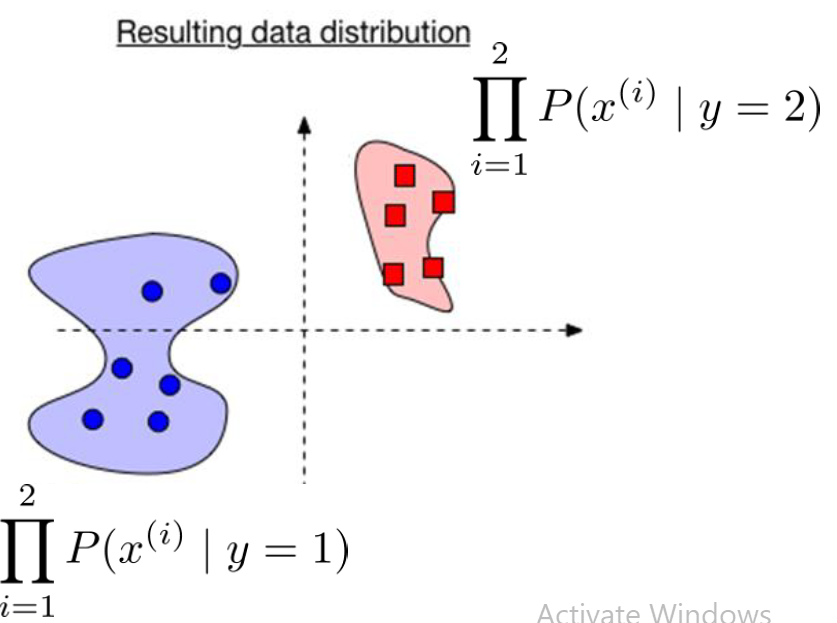
It is basically a Generative Classifier:

• Attempts to model class, that is, build a generative statistical model that informs us how a given class would generate input data.
• Ideally, we want to learn the joint distribution of the input x and output label y, that is, P( x ,y).
• For a test point, generative classifiers predict which class would have most likely generated the given observation.
• Mathematically, prediction for input x is carried out by computing the conditional probability P( y| x ) and selecting the most likely label y.
• Using the Bayes rule, we can compute P(y| x ) by computing P(y) and P(x |y).
• Estimating P(y) and P(x|y) is called generative learning.

Overview of Naïve Bayes Classifier:

We have \[
D = \{(x_1, y_1), (x_2, y_2), (x_3, y_3), \dots, (x_n, y_n)\}
\]
y={1,2,……,M} (M Class Classification)

Key Idea:

Estimate probability P(y|x) from data using Bayes Theorem.

Using Bayes theorem and MAP learning framework, we can write this as:

Estimating P(y) is easy. If y takes on discrete binary values, coin tossing, spam Vs non spam email detection for example, we simply need to count how many times we observe each class outcome.

Estimating P(x|y) however is not easy! Can You Guess WHY? 

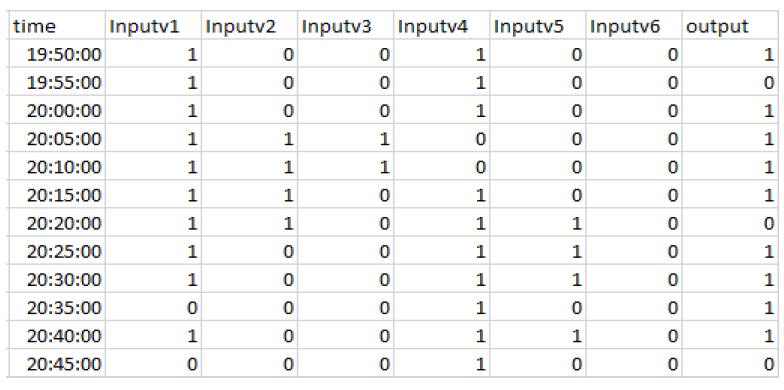
​Naïve Bayes Classifier-Example 

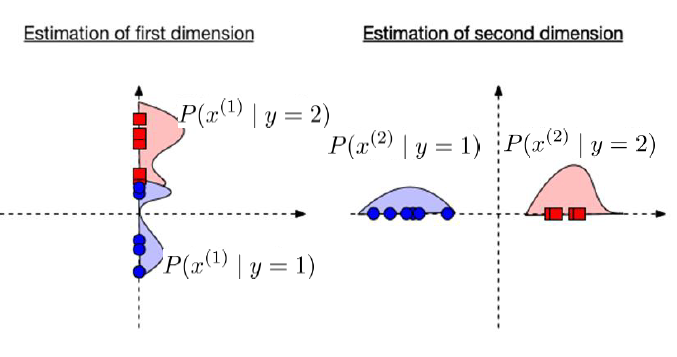
In this example We assume that M=2 and features d=6. Considering it to be a binary features classification. We want to estimate \[ P(x \mid y) = P\big(x^{(1)}, x^{(2)}, x^{(3)}, \ldots, x^{(6)} \mid y\big) \]

We need to represent all 2⁶ outcomes and probabilities for each y=0,1.

Learning the values for full conditional probabilities would require enormous amounts of data. To overcome this requirement of enormous amounts of data for the computation of conditional probability, we can make a Naive bayes assumption.

Features are mutually independent given the label. Hence we will have,

 

 

 

Another Example of Naive Bayes Classification

Imagine classifying a fruit as an apple or orange based on features like color (red or orange) and texture (smooth or bumpy):

• Training data: Apples are often red and smooth; oranges are orange and bumpy.
• Priors:
  $P(\text{Apple}) = 0.5$ 

  $P(\text{Apple})=0.5$, $P(\text{Orange}) = 0.5$ 

  $P(\text{Orange})=0.5$.

• Likelihoods:
  $P(\text{red}|\text{Apple}) = 0.8$ 

  $P(\text{red}|\text{Apple})=0.8$, $P(\text{red}|\text{Orange}) = 0.2$ 

  $P(\text{red}|\text{Orange})=0.2$, $P(\text{smooth}|\text{Apple}) = 0.7$ 

  $P(\text{smooth}|\text{Apple})=0.7$, $P(\text{smooth}|\text{Orange}) = 0.3$ 

  $P(\text{smooth}|\text{Orange})=0.3$.

• For a red, smooth fruit:
  • 
    $P(\text{Apple}|\text{red, smooth}) \propto 0.8 \cdot 0.7 \cdot 0.5 = 0.28$ 

    $P(\text{Apple}|\text{red, smooth})\propto 0.8\cdot 0.7\cdot 0.5=0.28$.

  • 
    $P(\text{Orange}|\text{red, smooth}) \propto 0.2 \cdot 0.3 \cdot 0.5 = 0.03$ 

    $P(\text{Orange}|\text{red, smooth})\propto 0.2\cdot 0.3\cdot 0.5=0.03$.

  • Classify as Apple (higher probability).

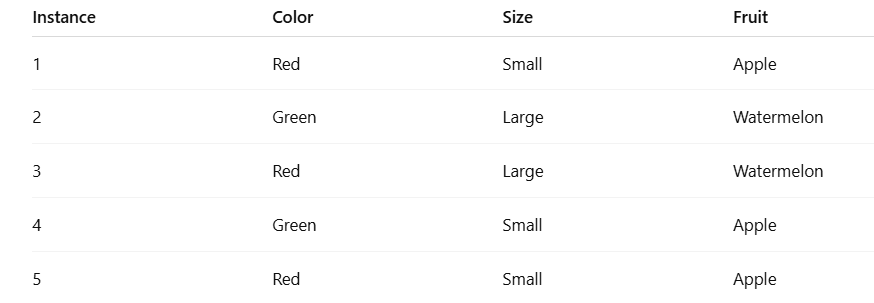
Here’s a unique Naive Bayes classification example presented in a tabular form, with a simple real-world scenario: classifying fruits as either Apple or Watermelon based on features Color and Size.

Training Data

Step 1: Calculate Prior Probabilities

P(Apple)=3/5,

P(Watermelon)=2/5

Calculate Likelihoods​

For Apple:

• $P(\text{Color=Green}|\text{Apple}) = \frac{1}{3}$P(Color=Green∣Apple)=31​

• $P(\text{Size=Small}|\text{Apple}) = \frac{2}{3}$P(Size=Small∣Apple)=32​

For Watermelon:

• $P(\text{Color=Green}|\text{Watermelon}) = \frac{1}{2}$P(Color=Green∣Watermelon)=21​

• $P(\text{Size=Small}|\text{Watermelon}) = \frac{0}{2} = 0$P(Size=Small∣Watermelon)=20​=0

Step 3: Classify a New Fruit

New fruit has features:

• Color = Green

• Size = Small

Posterior Probabilities:

• Apple:

   

  $$P(\text{Apple})\cdot P(\text{Green}\mathrm{\mid }\text{Apple})\cdot P(\text{Small}\mathrm{\mid }\text{Apple})=\frac{3}{5}\cdot \frac{1}{3}\cdot \frac{2}{3}=\frac{2}{\mathrm{15<span\; style="font-family:\; Georgia,\; \text{'}Times\; New\; Roman\text{'},\; \text{'}Bitstream\; Charter\text{'},\; Times,\; serif;"></span>}}$$ 

• Watermelon:

   

  $$P(\text{Watermelon}) \cdot P(\text{Green}|\text{Watermelon}) \cdot P(\text{Small}|\text{Watermelon}) = \frac{2}{5} \cdot \frac{1}{2} \cdot 0 = 0Prediction:$$ApplePrediction: Apple 

Prediction: Apple

Advantages

• Simple and Fast: Works well with small datasets and high-dimensional data (e.g., text classification).
• Scalable: Computationally efficient, especially for large datasets.
• Handles Missing Data: Can work with partial feature information.
• Good for Text Data: Excels in tasks like spam filtering or sentiment analysis.

Disadvantages

• Independence Assumption: Rarely true in real-world data, which can reduce accuracy.
• Limited Expressiveness: Struggles with complex relationships between features.
• Zero Probability Problem: If a feature value wasn’t seen in training, it assigns zero probability (mitigated by techniques like Laplace smoothing).

Applications of naive Bayes Classifier

• Text Classification: Spam email filtering, sentiment analysis, document categorization.
• Medical Diagnosis: Predicting diseases based on symptoms or test results.
• Recommendation Systems: Basic user preference modeling.
• Fraud Detection: Identifying anomalous patterns in transactions.