Formula for Newton’s Forward difference interpolation
How to derive formula for Newton’s Forward difference interpolation? Newton’s forward difference interpolation technique is used when the data points are equidistant. For the given set of data points we can develop Newton’s forward difference interpolation formula from newton’s divided difference formula. In this approach the finite divided differences are replaced by forward difference operator.
What is the forward difference operator?
The forward difference operator is denoted by Δ and it is the difference between two consecutive values of a function. Lets say we have a function y=f(x) having values
![]() corresponding to different values of x as
corresponding to different values of x as ![]()
then the first order divided difference is denoted as Δy0=y1-y0. Similarly the higher order divided differences can be shown in the following table
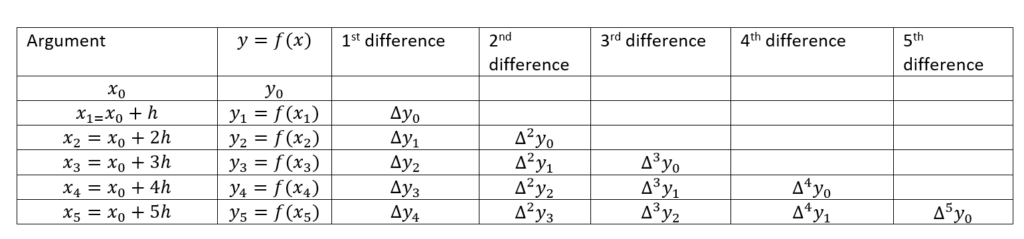
We can write the forward difference formula as:
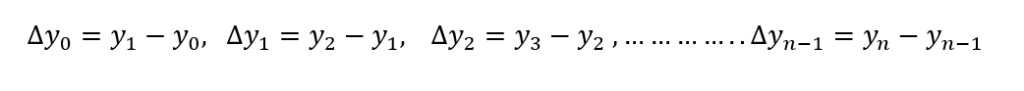
Develop the formula for Newton’s Forward difference interpolation from divided difference formula
For equidistant and ascending data points the Newton’s divided difference formula gives the coefficients of the polynomial as:
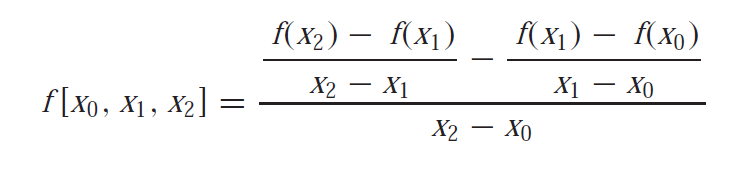
which can be simplified as
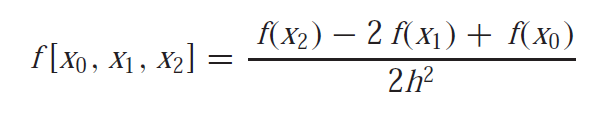
because
![]()
As we know that the second forward difference is equal to
![]()
Therefore we can write as
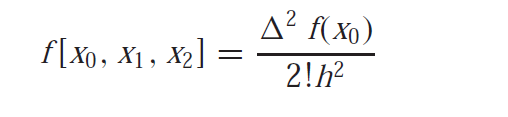
The generalization of this gives
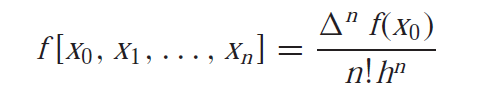
After substituting this into the newton’s divided difference interpolation formula, we get the expression of newton’s forward difference interpolation formula which is given as
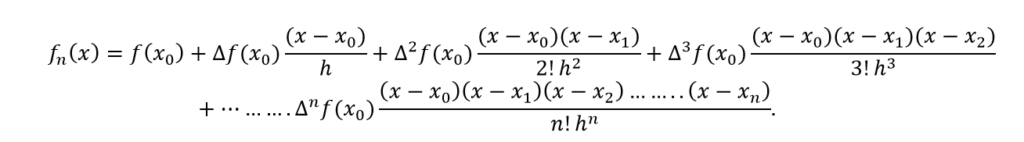
Also read here
https://eevibes.com/what-is-the-meaning-of-interpolation-what-are-the-types-of-interpolation/
One thought on “How to derive formula for Newton’s Forward difference interpolation?”