Formula for Newton’s Forward difference interpolation

How to derive formula for Newton’s Forward difference interpolation? Newton’s forward difference interpolation technique is used when the data points are equidistant. For the given set of data points we can develop Newton’s forward difference interpolation formula from newton’s divided difference formula. In this approach the finite divided differences are replaced by forward difference operator.

What is the forward difference operator?

The forward difference operator is denoted by Δ and it is the difference between two consecutive values of a function. Lets say we have a function y=f(x) having values

corresponding to different values of x as

then the first order divided difference is denoted as Δy0=y1-y0. Similarly the higher order divided differences can be shown in the following table

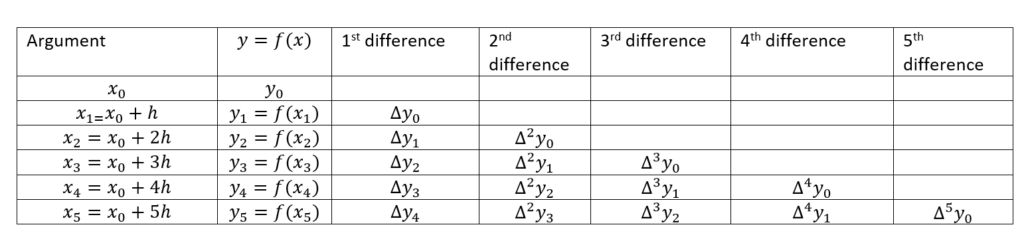
We can write the forward difference formula as:

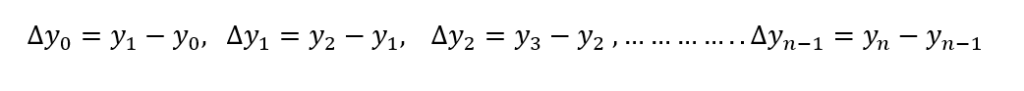
Develop the formula for Newton’s Forward difference interpolation from divided difference formula

For equidistant and ascending data points the Newton’s divided difference formula gives the coefficients of the polynomial as:

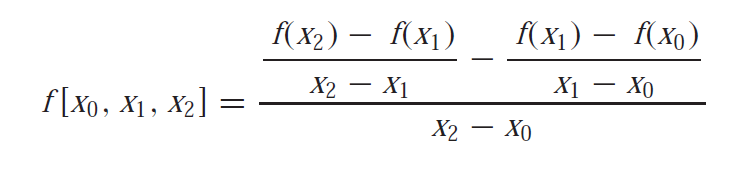
which can be simplified as

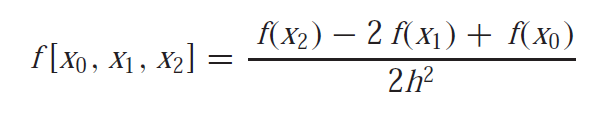
because

As we know that the second forward difference is equal to

Therefore we can write as

The generalization of this gives

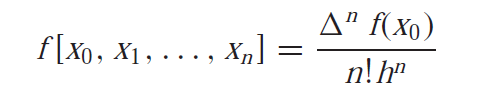
After substituting this into the newton’s divided difference interpolation formula, we get the expression of newton’s forward difference interpolation formula which is given as

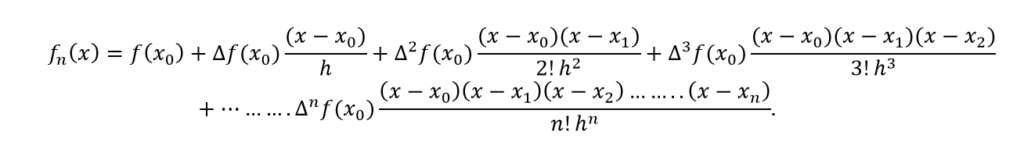
Also read here

https://eevibes.com/what-is-the-meaning-of-interpolation-what-are-the-types-of-interpolation/

What is the meaning of interpolation ? What are the types of interpolation? which interpolation technique should be used?