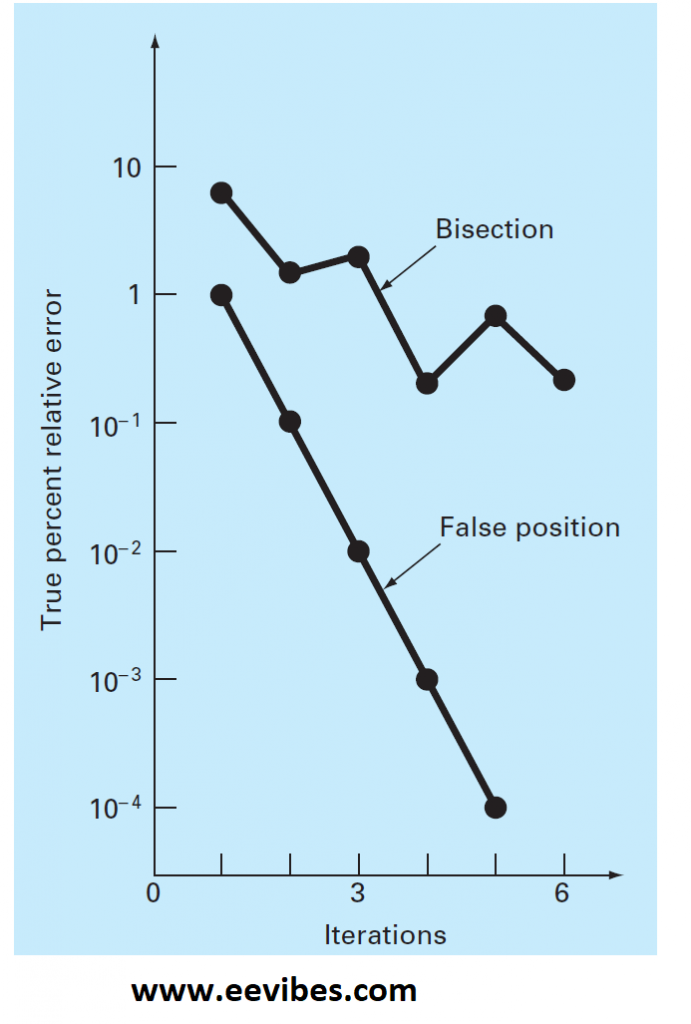
This is one of the iterative methods that give you the root if the function changes its sign: from positive to negative or from negative to positive. Despite the fact that bisection is an entirely legitimate strategy for determining roots, its “brute force” approach is generally inefficient. False position is based on graphical approach. A shortcoming of the bisection method is that, in dividing the interval from xl to xu into equivalent parts, no record is taken of the values of f (xl) and f (xu).