Introduction

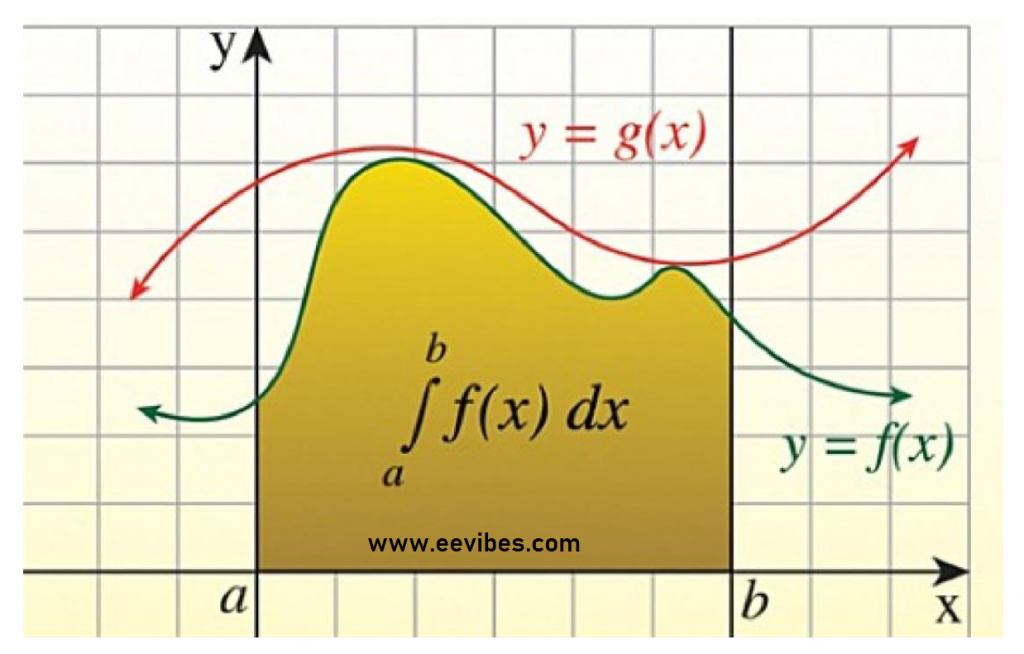
In calculus, integrals are used to find the volume and area of the region. This branch of calculus also provides graphs of the integral functions. Integral is used to solve the complex problems of calculus with respect to integrating variables.

In this post, we will learn the definition, formulas, types, and examples of integrals.

What is integral?

In mathematics, an integral assigns numbers to functions in a way that defines the area, displacement, volume, and other concepts that arise by joining the infinitesimal data.

The process of finding the integrals of the functions by applying the rules and formulas is known as integration. Integral is applied to the function by using an integral notation. The integral notation may or may not have upper and lower limits.

Formula of integral

The formulas of the integral can be used to integrate the functions with or without taking the limits. The equation used for integral is given below.

ʃ f(x) dx

• The integral notation used to integrate the function is ʃ.
• f(x) is the function.
• dx is the integrating variable.

Types of integral

The types of the integral are used to integrate the function with or without using the limits. In integral calculus, there are two types of integral.

1. Indefinite integral
2. Definite integral

1.    Definite integral

The definite integral is the other type of integral. It is used to integrate the functions by taking the upper and lower limits of the function. This type of integral integrates the function first and then applies the limits according to the fundamental theorem of calculus.

The equation used to integrate the function using a definite integral is given below.

ʃf(x) dx = F(b) – F(a) = L

• In a and b are the lower and upper limits respectively and it is known as the integral notation of definite integral.
• f(x) is the given function.
• dx is the integrating variable.
• F(b) – F(a) is the fundamental theorem of calculus.
• L is the result of the definite integral.

1.    Indefinite integral

the indefinite integral is used to integrate the integral without taking the upper and lower limits of the function. In this type of integral, integrate the function and write the integral with the constant of integration.

The equation of indefinite integral is given below.

ʃ f(x) dx = F(x) + c

• The integral notation used to integrate the function is ʃ.
• f(x) is the function.
• dx is the integrating variable.
• F(x) is the integral of the function.
• C is the constant of integration.

You can use an integral calculator to integrate the functions according to the above types of integral.

Examples of integral

Following are a few examples of integral solved by using the types and formulas of integral.

Example 1: For indefinite integral

Calculate the indefinite integral of 6x³ + 7cos(x) – 12x³y² + xy – cot(x) having x as an integrating variable.

Solution

Step 1: Use the integral notation to write the given function.

ʃ (6x³ + 7cos(x) – 12x³y² + xy – cot(x)) dx

Step 2: Now use the rules of integration to apply the integral notation separately.

ʃ (6x³ + 7cos(x) – 12x³y² + xy – cot(x)) dx = ʃ (6x³) dx + ʃ 7cos(x) dx – ʃ 12x³y² dx + ʃ xy dx – ʃ cot(x) dx

Step 3: Use constant function rule and write the constant outside the integral notation.

ʃ (6x³ + 7cos(x) – 12x³y² + xy – cot(x)) dx = 6 ʃ (x³) dx + 7 ʃ cos(x) dx – 12 y² ʃ x³ dx + y ʃ x dx – ʃ cot(x) dx

Step 4: Now use the power and trigonometric rules to integrate the above equation.

ʃ (6x³ + 7cos(x) – 12x³y² + xy – cot(x)) dx = 6 (x³⁺¹ / 3 + 1) + 7 (sin(x)) – 12y²(x³⁺¹ / 3 + 1) + y (x¹⁺¹ / 1 + 1) – ln(sin(x)) + C

ʃ (6x³ + 7cos(x) – 12x³y² + xy – cot(x)) dx = 6 (x⁴ / 4) + 7 (sin(x)) – 12y² (x⁴ / 4) + y (x² / 2) – ln(sin(x)) + C

ʃ (6x³ + 7cos(x) – 12x³y² + xy – cot(x)) dx = 6/4 (x⁴) + 7 (sin(x)) – 12y²/4 (x⁴) + y (x² / 2) – ln(sin(x)) + C

ʃ (6x³ + 7cos(x) – 12x³y² + xy – cot(x)) dx = 3/2 (x⁴) + 7 (sin(x)) – 3y² (x⁴) + y (x² / 2) – ln(sin(x)) + C

ʃ (6x³ + 7cos(x) – 12x³y² + xy – cot(x)) dx = 3x⁴/2+ 7sin(x) – 3 x⁴y² + x²y/ 2 – ln(sin(x)) + C

Example 2: For definite integral

Calculate the definite integral of 15x⁴ + 2cos(x) – 5x⁴y³ + 15x² having x as an integrating variable and limits of x are from 2 to 5.

Solution

Step 1: Use the integral notation to write the given function.

(15x⁴ + 2cos(x) – 5x⁴y³ + 15x²) dx

Step 2: Now use the rules of integration to apply the integral notation separately.

(15x⁴ + 2cos(x) – 5x⁴y³ + 15x²) dx = (15x⁴) dx + (2cos(x)) dx – (5x⁴y³ dx + (15x²) dx

Step 3: Use the constant function rule and write the constant outside the integral notation.

(15x⁴ + 2cos(x) – 5x⁴y³ + 15x²) dx = 15(x⁴) dx + 22cos(x) dx – 5y³(x⁴ dx + 15(x²) dx

Step 4: Now use the power and trigonometric rules to integrate the above equation.

(15x⁴ + 2cos(x) – 5x⁴y³ + 15x²) dx = 15 (x⁴⁺¹ / 4 +1)⁵₂ + 2 (-sin(x) )⁵₂ – 5y³ (x⁴⁺¹ / 4 +1)⁵₂ + 15 (x²⁺¹ /2 + 1)⁵₂

(15x⁴ + 2cos(x) – 5x⁴y³ + 15x²) dx = 15 (x⁵ / 5)⁵₂ + 2 (-sin(x) )⁵₂ – 5y³ (x⁵ / 5)⁵₂ + 15 (x³ / 3)⁵₂

(15x⁴ + 2cos(x) – 5x⁴y³ + 15x²) dx = 15/5 (x⁵)⁵₂ + 2 (-sin(x) )⁵₂ – 5y³/5 (x⁵)⁵₂ + 15/3 (x³)⁵₂

(15x⁴ + 2cos(x) – 5x⁴y³ + 15x²) dx = 3 (x⁵)⁵₂ – 2 (sin(x) )⁵₂ – y³ (x⁵)⁵₂ + 5 (x³)⁵₂

Step 5: Use the fundamental theorem of calculus to get the result.

(15x⁴ + 2cos(x) – 5x⁴y³ + 15x²) dx = 3 (5⁵ – 2⁵) – 2 (sin (5)) – sin (2))) – y³ (5⁵ – 2⁵) + 5 (5³ – 2³)

(15x⁴ + 2cos(x) – 5x⁴y³ + 15x²) dx = 3 (3125 – 32) – 2 (-0.9589 – 0.9093) – y³ (3125 – 32) + 5 (125 – 8)

(15x⁴ + 2cos(x) – 5x⁴y³ + 15x²) dx = 3(3093) – 2 (-1.8692) – y³ (3093) + 5 (117)

(15x⁴ + 2cos(x) – 5x⁴y³ + 15x²) dx = 9279 + 3.7364 – 3093y³ + 585

(15x⁴ + 2cos(x) – 5x⁴y³ + 15x²) dx = 9867.7364– 3093y³

Summary

In this article, we have learned about the definition, formulas, types, and examples of integral. Now you can solve any problem of antiderivatives by learning this post.

Also read here

https://eevibes.com/mathematics/numerical-analysis/describe-and-develop-the-formula-for-newtons-forward-difference-interpolation/

How to derive formula for Newton’s Forward difference interpolation?