Table of Contents

Introduction to Metaheuristic Algorithm

How to Design Combinational Logic Circuits by using Metaheuristic Algorithm? Designing of combinational logic circuits is a dual problem. We have to make sure that the design is 100% functional and also, it must be an optimal design using minimum number of gates to avoid complicated circuits.

The research will be on a new algorithm called Metaheuristic Algorithm that is used for the designing of very large combinational circuits using minimum number of gates. This algorithm uses the exploration power of heuristic search to create method of solving designing problems. The proposed algorithm is verified by applying 12 inputs to 4 various problems.

Previous Work:

The logic circuit design is seen – just like any other design work – as a clever act. Several researchers have addressed this issue using various metaheuristic methods. One of the most frequently used metaheuristic devices is genetic algorithms. However, since genetic algorithms are demographic, it seems difficult to solve the problem with the large number of entries as the chromosome size increases and computer time increases dramatically.

Miller et al used genetic algorithms to convert digital circuits, some of these circuits into one subset, two bit adders with carry and three and four bits.

Miller et al also developed an Intrinsic evolvable hardware platform (IEHW) in which the evolutionary process was much faster compared to software or VHDL simulation. partiality is part of the work of fitness for strength.

Cecelia et al also proposed a GA design for intelligent circuits, and used this algorithm to design circuits such as 2 to 1 multiplexers and a check for a minimum of four.

The concept of the novel was introduced by Hounsell et al, as they developed an evolutionary algorithm capable of transforming and testing circuits in the language of Computer Descriptions (HDL) in a novel space they call a visual chip.

One researcher has used other Artificial intelligence algorithms on their own or in combination with evolutionary algorithms, as in [11] Moore et al. introduced an algorithm used to design compact intelligent circuits, their algorithm was inspired from quantum evolution and realistic Swarm, claiming the superiority of their hybrid algorithm over other active swarm algorithms and other evolutionary algorithms such as- GA.

Colello et al demonstrated a design strategy that combines sensible circuits that produce circuits with a smaller number of gates than those produced by human designers, and what is interesting in their research is that they analyze the solution produced by GA and note that GA tried to significantly reduce it. number of gates as if using De Morgan Rules or any other Boolean simplification method that can be used to teach students what steps to follow to make it easier to proceed with a particular solution.

What is Metaheuristics?

In the real world, lumbering elephants are exposed by the aggression of speeding midgets. For these types of complex problems, heuristics and metaheuristics are often used.

Metaheuristics is a subset of heuristics and is based on artificial intelligence (AI) to improve its heuristic approach [3], however it is not guaranteed to find a superior solution. Metaheuristics includes standardized measurement.

Tabu Search (TS), Genetic algorithms and Swarm intelligence. Tabu Search is a metaheuristic method originally proposed by Glover in 1986. Two major procedures that are usually applied during Tabu search; Intensification and Diversification.

The idea behind the concept of search reinforcement is that, as a smart person might do, one should carefully examine the parts of the search space that seem “promising” to ensure that the best solutions in these areas are real found.

Diversification is an algorithmic method that attempts to alleviate this problem by forcing searches in previously unchecked areas of the search space. It is usually based on some kind of long-term search memory.

We can design and explain any of the combinational logic circuits by using a switching logical expression (AND, OR, NOT) but it is also mandatory to simplify the stated logical expression to its minimal form to reduce the number of gates in order to reduce the cost of circuit and increase the accuracy of the circuit design.

The simplification of the expression can be performed by various methods like Consensus Theorem but there are no rules for applying this simplification method.

K-Map and Quine-McCluskey procedures can be used to overcome the drawbacks of Consensus theorem. K-map can be used to simplify expression having 5 to 6 variables, but in case of more than 6 variables k-map is very difficult to apply because it is hard to mark pattern for solution in multidimensional space. While in Quine McCluskey logical expression can be reduced by following steps:

Determining the essential prime implicants.
By choosing minimal set of prime implicant to cover function.

But for n=32, the prime implicant can be 600 trillion. For this problem Metaheuristic Algorithm is applied.

Heuristic and metaheuristic techniques should be used in this design problem where arithmetic operations are not working and a good solution, although not guaranteed to be high is still satisfactory.
In this paper we introduce a new metaheuristic algorithm to make a process that can be used to make meaningful speech easier in practice and can be used in larger integrated circuits.
The paper is designed as follows, the current section is a presentation section that gives a brief overview of the hypothetical problem, the second section discusses a common metaheuristics perspective with additional concerns about Tabu Algorithms.
The third phase provides a quick overview of the ongoing work followed by the fourth phase which discusses the proposed algorithm followed by the phase of the test cases used to validate the algorithm, the final phase concludes the study.

The structure of the design solution using a new metaheuristic algorithm will be the total product (SOP), similar to the structure provided by both k-maps and Quine-McCluskey processes.

Some of the terminologies used in this algorithm are:

Complexity: The total number of logic OR and AND

operations in expression.

Term: The product of variables entity in SOP
Tabu Term: A term is considered as a Tabu term if its outputs is 1 at any bit location that is required to be a “0”, using the SOP form, the functional logic expression would never have a Tabu term as the effect of a wrongful 1 can never be undone with other
Fitness (F): The fitness of each candidate solution is the ratio of correct bits produced by the solution compared to the required output bit A solution with 100 fitness is a functional solution.
Term Fitness: The fitness value of each Term in the G-Term Set is based upon the total number of ones that came from the Term on its evaluation, the higher the number of ones the higher the This Term Fitness serves as the Heuristic value for each Term.
G-Term set: If the term is not a Tabu term, it is added to the G term Set. This set is a sorted set where there are no identical terms as members of this Each term in the G term set has its own fitness.

Methodology:

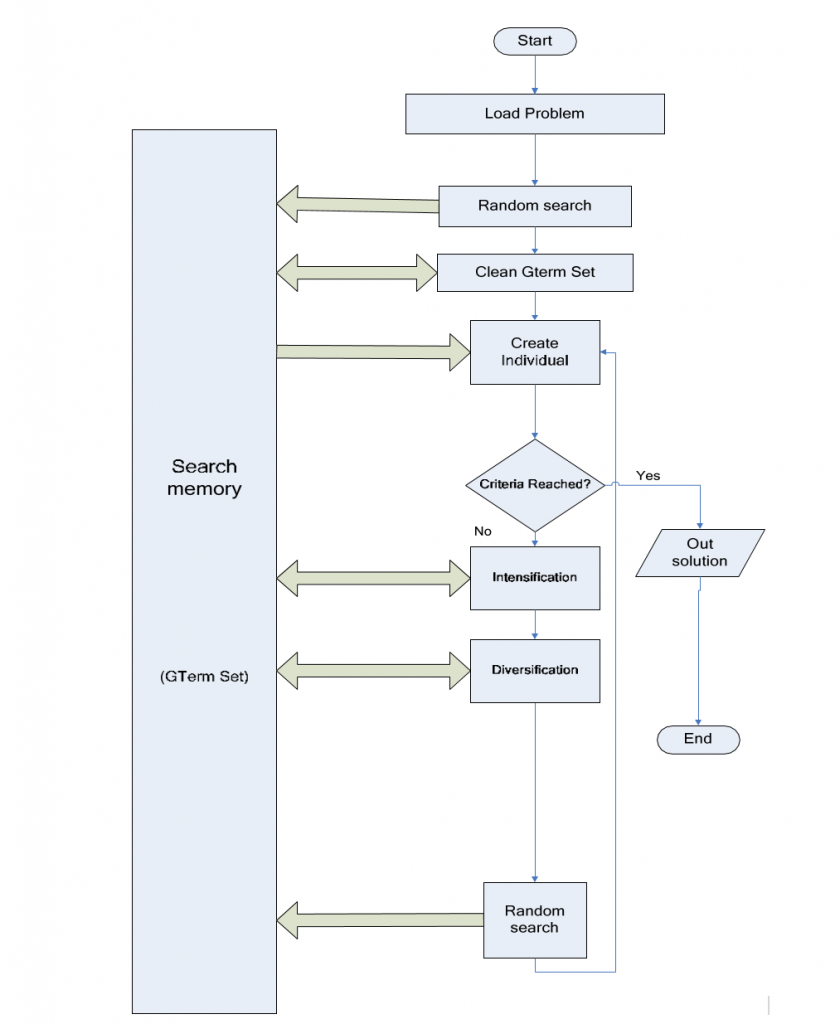
The main theme of the proposed algorithm is to eliminate the problem of finding the required expression in the number of small problems finding the right words. Search memory is a Gterm set, as long as it is updated individually it will be updated individually. The problem is loaded as a text file containing a series of 0s and 1s output that you want. Random search is done to get information about the problem and start completing the G-Term set. Update G-Term Set using the Clean-G-Term process. Man is created using the Update Individual process. If the required qualifications and complexity are met, or if a certain number of repetitions passes without improvement, the search stops and goes to step ten otherwise the search will proceed to the next step. Stabilization is performed on a G-Term set using the remove variable process. Verification is done using the Verify process. Random searches are also performed – similar to step 2 – as a test method.

Go back to step three, hence solution is declared. The algorithm is based on following procedural points:

Random Search: people are created randomly in the SOP way and your suitability is checked, each word randomly builds in 2 aspects: –
(C1): No problem flexibility should be minimized at the same time.
(C2): No problem variation should be present in the term and its coherence.
Individual Examination: This process assesses each individual by checking all of its terms, as each term is tested, to see if it will be considered a Tabu Term or can be added to the G-term set.
Clean G-Term: In any of the 2 terms Term1, Term 2 in the G-term set. If Term1 is completely contained in Term2. Then Term2 is released on the G-term set. For example if both A’BC and A’BCD are present in the Gterm set, then this process will remove A’BCD from the set. As a matter of fact A’BC is less complex and will get a higher number of those on exit than A’BCD.
Remove Variable: this process is applied to each term in the G-term set. It aims to improve the suitability of each term by removing the physical variables from it. For example B’FGH may be converted to B’GH if it later has a better fit.
Update Individual: the person to be written by created by SOP from all the principles in the G-term set.
Verify: Variable inputs that do not appear within the terms of the G-Term Set are reported. Man is created using Random Search, however creation is biased to increase the likelihood of those changes.

block diagram of Metaheuristic Algorithm

Results:

Case 1:

Four different problems were used to test the validity of the algorithm, each with 12 input equations. Table I reports on these problems and the frequency with which they found solutions to each problem.

The proposed algorithm was able to solve all the test scenarios, the first problem has medium size terms and the variations of each input only appear once.

Case 2:

In the second problem, some of the input variables are “indifferent” and the proposed algorithm succeeded in removing it from the declared high resolution, the third problem was used to test the ability to find long and short words. The fourth problem – which has been solved for a very long time – has been responsible for variable dynamics (A) and variable dynamics.

Problem	Iteration
A.B’.C+D’.E’.H’.I+J’.K.L.F’.G	18
A.B’.C+E’.H’+J’.L.F’.G	13
A.B’+C+D’.E’.H’.I.J’.K.L.F’.G	12
A.B’.C+A.D’.E’.H’.I+B’.J’.K.L.F’.G	43

Conclusion:

An automatic metaheuristic novel algorithm for the process of assembling a logical circuit design is introduced, The algorithm uses a flexible structure while changing the logical expression and total product structure. The proposed algorithm is based on Tabu Search, special processes designed for bias and the final solution to have only the most important features.

Combining the power of random search experiments with the use of Tabu search memory and heuristic to measure the relevance of each term in a logical quote, has created a valid algorithm for problem-solving design for large integrated logical circuits.

Future Work:

The future work of this research paper is that we can use the metaheuristics algorithm to simply those combinational logic circuits that cannot be simplified by using K-map or other techniques. Meta-heuristic algorithms are highly relevant and powerful tools for solving complex problems. However, the most important thing to remember is that the performance of many algorithms published even in reputable journals is very poor. In contrast, some algorithms (such as WOA) have excellent performance on a wide range of problems (structural problems or high-volume even larger than 10,000!). In our opinion, it seems necessary to create a database to verify the accuracy of the methods (their computer codes) introduced today. In this way, a specific hyper-heuristic process can be created, in which the content of the problem is examined and the appropriate solution is selected. However, the reason for providing new methods of meta-heuristics can be explored with two perspectives.