Introduction
how to represent Boolean functions in class of reversible logic circuits? Specifically, we are talking about an algorithm for constructing minimal representation of multiple-output Boolean functions in reversible logic circuits. Our research will be on the problem that is the representation of Boolean functions in class of reversible logic circuits. Each Boolean function is implemented by reversible logic circuit. Reversible circuits are built with Toffoli elements.
Operators are also used for description of representation; specifically special operator form (SOF) is used. Certain operators are used for the construction of Boolean’s SOF. The corresponding multiple-output reversible function and operators of SOF are used to define the minimal reversible circuit for a given Boolean function
Zhegalkin polynomials are used for construction of reversible logic circuit. There’s always a need for growth, a desire of something new. For modern computers, an acceleration of processing, storage and data transfer is always appreciated. This aim can be achieved but the problem is reversible representation of Boolean functions. To minimize the representation of Boolean functions in classes of polynomial normal forms we have used different methods: First, we have used operator approach in polynomial normal form that has to be effective. Another method is described for computing the complexity of the representation of Boolean function’s special operator form in the class of single-generated operator’s bundles with a fixed operator at the beginning of the bundle, and an algorithm for finding the minimal representation of functions in the class of Kronecker forms is proposed.
In this article minimization of representation of Boolean function in reversible logic circuit is based on the methods as mentioned.
BACKGROUND:
Operator representations of functions:
For a standard Boolean function following conventions and notations are used: The following conventions and notations to be used for standard Boolean functions:
1) Arguments and values of Boolean functions are selected from the set {0,1}.
2) –x – negation function.
3) x ⋅ y – conjunction function.
4) x ⊕ y – exclusive-or sum function.
Later, operators are discussed in more detail.
The operator is represented by a sequence of the form b = b1…bn, where bj∈{e, p, d}. The components bj of the operator b act on the function f(x1,…, xn) with respect to the arguments xj; e is an identity operator, p is a negation operator for the variable, d is the operator for taking the derivative.
Example. Let b=pped, f (x1, x2, x3, x4) = x1 ⋅ x2 ⋅ x3 ⋅ x4 then
bf (x1, x2, x3, x4) = pped (x1 ⋅ x2 ⋅ x3 ⋅ x4) = ppe(x1 ⋅ x2 ⋅ x3 ⋅0 ⊕
x1 ⋅ x2 ⋅ x3 ⋅1) = ppе (x1 ⋅ x2 ⋅ x3) = -x1 ⋅ -x2 ⋅ x3.
The set of operators A = (a0 …, aN) consisting of 2n operators of length n is called an operator bundle. Consider the images of the bundle operators with respect to some function g (x1…, xn) form a basis of the linear space Bn of all Boolean functions, then the bundle is a basis. The operator bundle A = (a0 ,…,aN) is called single-generated if there are such operators b = b1…bn and c = c1…cn, bj ≠ cj for any j that the t k = t1…tn operator of a bundle A is defined as follows: tj = bj if j-th bit in binary notation of number k is equals to 0, and tj = cj if j-th bit in binary notation of number k is equals to 1.
Let b be an operator of length n. We construct the class Kb of single-generated operator bundles Ai= a0, i, …, aN,i) such that b = a0,i, running through all i from 0 to 2n – 1. Then the class Kd…d corresponds to a well-known class of Reed–Muller forms or polarized Zhegalkin polynomials, which will be considered below. We denote this class by Zh. The binary representation of the index i is the polarization vector. For example, for n = 2, the class Zh = Kdd contains bundles:
A0 = {dd, dp, pd, pp}.
A1 = {dd, de, pd, pe}.
A2 = {dd, dp, ed, ep}.
A3 = {dd, de, ed, ee}.
The operator c is called the sum of the operators a and b if the following equality holds for any function f (x1…., xn): cf(x1,…, xn) = af(x1,…, xn) ⊕ bf(x1,…, xn). For the bundle Ai from Zh we compose the operator ci represented by the sum of the operators of the bundle Ai [1]. We denote by ZhiE the class of operator bundles C ⊂ Ai ∪ {ci} such that the cardinality of each of them is equal to 2n and we call it the i-th class of the extended polarized Zhegalkin polynomials. The union of the classes ZhiE is the class ZhE of the extended polarized Zhegalkin polynomials.
Let the function f (x1…, xn) have the following operator form in the single-generated operator bundle A: OF(f)=a1 (x1 ·…· xn) ⊕ … ⊕ as (x1 ·…· xn), where ak from A. Instead of the operators ak in the form OF(f), we substitute the sum of the operators of the corresponding single-generated operator bundle, we reduce the same terms and obtain a representation for the function f (x1…, xn), which is called a special operator form and will be denoted by SOF(f). The uniqueness of SOF(f) for a function f is proved in [3]. The special operator form SOF(f) allows us to construct the operator form Oi(f) in any of the bundles of the operators Ai from any Kb. We shall consider only the classes Zh and ZhE.
Let L(Oi) be the number of terms in the operator form Oi. Then the complexity of the function f (x1…, xn) in the class Zh is equals to: LZh(f) = minOiL(Oi), over all forms Oi(f) compiled with respect to bundles of class Zh.
Reversible representations of Boolean functions:
For any Boolean function f (x1…, xn) may be represented by a reversible (n+1, n+1)-function F (x0, x1…, xn) that give one-toone mapping from the set {(a0, a1…, an)} to the set {(a0⊕ f(a1…,an), a1,…,an)}. In more detail all the necessary definitions are given in [4, 5]. We denote Y by the set of reversible functions of the form F (x0, x1…, xn). We consider the set T of reversible functions (called the Toffoli function [6]) of the following form:
1) T1 n+1(xi):
(x0, x1…, xi …, xn) → (x0, x1…, -xi…, xn), i∈ {1…,n};
2) Tk n+1((xi1…, xik, x0):
(x0…, xn) → (x0⊕xi1⋅…⋅xik, x1…, xn), k > 0,
{i1…,ik}⊆{1,…,n}. We denote by [T] the set of all invertible functions that can be represented as a superposition of functions of the set T. Theorem 1. Y ⊂ [T]. Let RS be the class of reversible circuits that are constructed from Toffoli elements and realized functions of the form F. Then the complexity of the function F is defined as follows: LRS(F) = minSL(S), running through all reversible circuits S in the class RS realizing the function F. Theorem 2. LRS(F) = minOi{min{L(Oi) + 2(n-w(i)); 2n + 1 + 2n – L(Oi)}}, w(i) is the number of units in the binary representation of i. If the function f is represented by a polarized Zhegalkin polynomial or its extended polynomial, then from the proof of Theorem 2 we derive a method for constructing a reversible circuit realizing the function F.
DESCRIPTION OF THE ALGORITHM
Building a library:
The work of the minimization algorithm is based on the pre-built library P. The library P is a matrix in which the columns are denoted by all possible operators b = b1…bn, bi ∈ {e, p}, and the rows are all possible operators a = a1…an, ai ∈ {e, p, d}. Columns of the matrix represent the expansion coefficients of the operators in the headers, in terms of the row operators. Theorem 3. The matrix P can be represented in the form of a Kronecker product of matrixes:
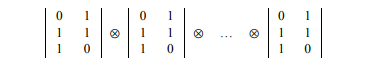
and it has a fractal structure.
Fig. 1 illustrates the matrix P for n=5, the units of the matrix are represented by filled rectangles, the empty spaces denote zeros.
The algorithm for constructing the library is based on Theorem 3. For small values of n (depending on the ability to load the library into the RAM), advanced matrix is constructed in it, using the decomposition of the matrix into the Kronecker product. If it is not possible to load the entire library into the RAM while the minimization algorithm is running, then the properties of the fractal matrix structure allow us to dynamically construct the necessary columns of the matrix.
Building SOF
The standard specification of a Boolean function in the form of a vector implies that there is already an expansion in the single-generated bundle (e … e, …, p … p). In this case, the generation of SOF(f) is reduced to performing the xor operation on the corresponding columns of the matrix P,a which are either already chosen or present in the table.
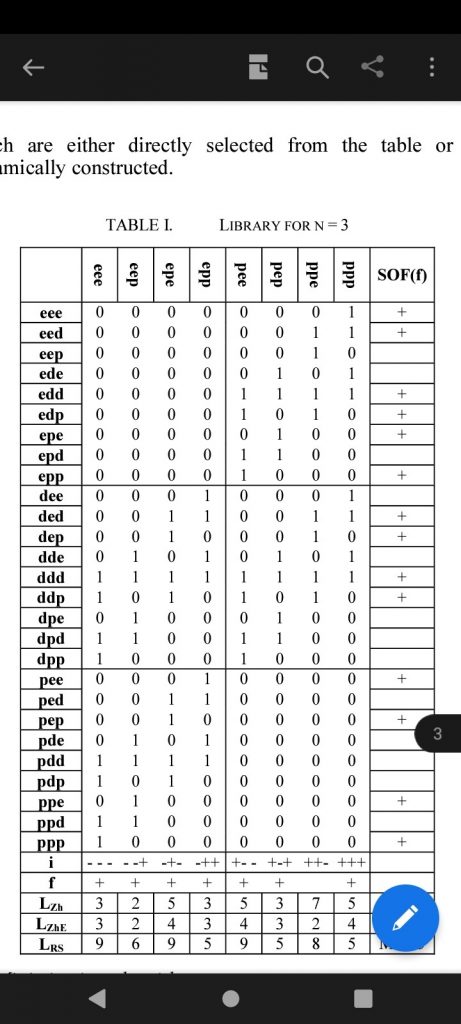
Key steps of minimizing the algorithm:
The minimization of algorithm is done through a pseucode;
- Int min_ bool _ reversible_ex(f)
1.vars. bools [m]; vector SOF(f)
2.bool. P M I. Library
3.int Q, N_Q, N ,a , Nx, Qx;

Future use:
The reversible logic gates use less energy consumption which reduce the power consumption and propogation delay which increase the speed of process.
Also read here
https://eevibes.com/digital-logic-design/how-to-design-a-4-bit-magnitude-comparator-circuit/