How to Simplify a Boolean Function Using Karnaugh Map (k-map)?
How to simplify a Boolean function using Karnaugh map (k-map)? Truth table representation of a function is always a unique expression. The complexity of a digital circuit can be reduced by just simplifying its Boolean expression. The more we reduce the redundant terms, the more simplified the digital circuit we have. One of the finest methods is the Karnaugh map.
In this method, the minterms are represented in a block of box. The size of the box is determined from the number of literals of a functions. If there are n literals, then there will be 2n possible blocks in a box. K-map method can be used from 2,3,4,5,….n variables. But because of the complexity of higher terms, we will just focus on upto four variables k-map. The k-map representation of a function is not unique. There can be different forms of a simplified function but each will contain equal number of literals.
2-variable k-map
The 2 variable k-map consists of four block where each block represents the minterm of a function. 2-variable k-map is shown below
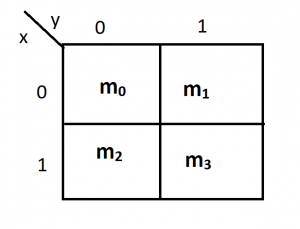
It can be seen clearly that each block is representing a minterm. m0 is adjacent to m1 and m2. Similarly, m3 is adjacent to m2 and m1.
Two adjacent terms can be combined to get a simplified expression. Since adjacent terms change only one bit at a time. So this property helps to simplify the Boolean expression. Minterms can be combined horizontally, vertically, in squares, from edges. Only terms of the order of 2n can be combined. No diagonal terms can be considered as adjacent terms.
Examples of 2-variable k-map
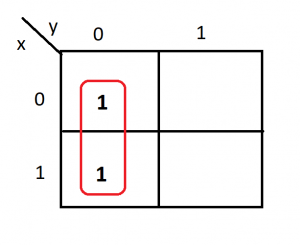
In terms of summation of minterms this function is equal to F=x’y’+xy’
The simplified function expression is
F(x,y)=y’
since 0 is marked as primed variable. y=0 in selected column so mention it as y’. x changes its value from 0 to 1. so (x+x’)y’=y’ given that x+x’=1. Both results can be compared and it can be concluded that original function needs four literals, while simplified version needs only one literal.
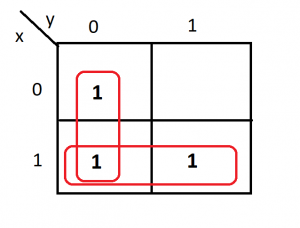
In this example function is equal to
F(x,y)=y’+x
Since vertical adjacent terms only produce y’ and the horizontal adjacent terms are corresponding to row where x=1.
It should be noted that if all minterms of the function are equal to 1 then this represents an identity/constant function or F=1.
3-variable k map
The three variable k-map will consist of 8 blocks. The minterms are mentioned in such a way that each adjacent block changes only one bit at a time as shown below.
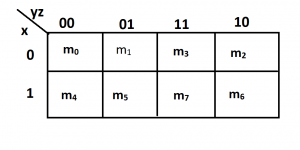
so if you notice m1 and m3 only change their 2nd bit (y 0—-> 1). This property causes the redundancy of Boolean expressions.
Examples of 3-variable k-map
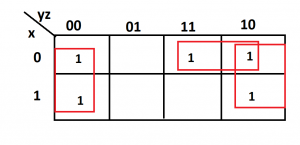
This function is simplified as
F=z’+x’y
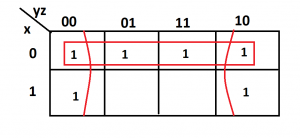
This function is simplified as
F=x’+z’
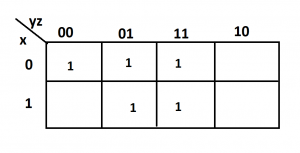
Solve some questions
4-variable k-map
The minterms of 4-variables k-map are represented as
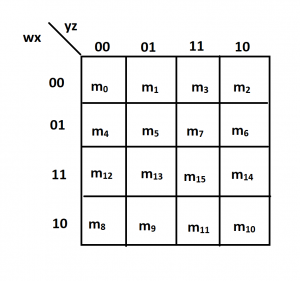
Lets say we are given the following minterms of a function
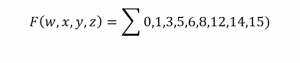
Now lets just simplify it using k-map. Place 1 in all boxes corresponding to the given minterms.
Answer
F=w’x’y’+w’y’z+w’x’z+wy’z’+wxy+xyz’
What are the Prime Implicants and Essential Prime Implicants?
The prime implicants in the K-map are obtained by joining the maximum possible adjacent squares of order of 2n. If a prime implicant covers a minterm in a square only once, then such prime implicant is called as essential prime implicant.
The prime implicants of a function can be obtained from the map by combining all possible maximum numbers of squares. This means that a single 1 on a map represents a prime implicant if it is not adjacent to any other 1’s. Two adjacent 1’s form a prime implicant, provided that they are not within a group of four adjacent squares. Four adjacent 1’s form a prime implicant if they are not within a group of eight adjacent squares, and so on. The essential prime implicants are found by looking at each square marked with a 1 and checking the number of prime implicants that cover it. The prime implicant is essential if it is the only prime implicant that covers the minterm.
How to Determine the Prime and Essential Prime Implicants of the Given Function?
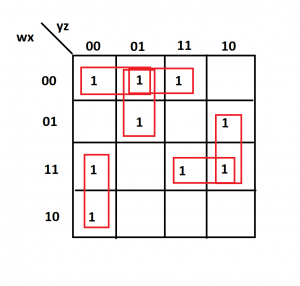
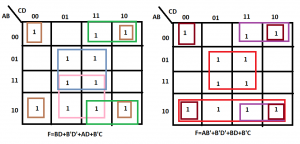
F(A, B, C, D) = Σ (0, 2, 3, 5, 7, 8, 9, 10, 11, 13, 15)
The four possible combinations of adjacent squares with their functions are shown below. It can be seen that BD and B’D’ are common in all four expressions:
F = BD + B’D’ + CD + AD
F= BD + B’D’ + CD + AB’
F= BD + B’D’ + B’C + AD
F= BD + B’D’ + B’C + AB’
That’s why they are essential prime implicants in the representation of function. The remaining are merely the prime implicants.
Video lecture for Karnaugh map (k-map) simplification method
here is the link of video lecture for simplifying a Boolean function using k-map
Software to simplify the Boolean expression
Software to simplify the Boolean expression using k-map
Example for Finding the Prime Implicants and Essential Prime Implicants
Simplification of Boolean Function with Karnaugh map using dont care Conditions
Also read here
https://eevibes.com/digital-logic-design/how-to-represent-the-boolean-function-in-canonical-form/
what is the Canonical form representation of Boolean function?