How to represent the Boolean function in Canonical form?
what is the Canonical form representation of a Boolean function? The canonical representation of a Boolean function can be of two forms.
- Summation of minterms
- Product of maxterms
In order to represent the function into these canonical forms, it is necessary that each term must contain all the literals that are involved for representing the function. Lets see first what is the meaning of minterms and maxterms.
What is the minterm representation?
The minterm is obtained if all literals of a function are combined with an AND gate operation. The literals may appear either in prime or unprimed form. While representing a minterm, 0 is written as primed and 1 is written as unprimed number. For n=3 variables (x,y,z) there are 2n=23=8 possible minterms that can be written as follows
| x | y | z | Minterms (mj) | Minterms |
| 0 | 0 | 0 | m0 | x’y’z’ |
| 0 | 0 | 1 | m1 | x’y’z |
| 0 | 1 | 0 | m2 | x’yz’ |
| 0 | 1 | 1 | m3 | x’yz |
| 1 | 0 | 0 | m4 | xy’z’ |
| 1 | 0 | 1 | m5 | xy’z |
| 1 | 1 | 0 | m6 | xyz’ |
| 1 | 1 | 1 | m7 | xyz |
What is a maxterm representation?
In maxterm representation, 0 is marked as unprimed and 1 is marked as primed variable. Also all the variables are involved with OR operation in their representation and these maxterms terms are then ANDED to form a Boolean function. Lets have a look of the following table.
| x | y | z | Maxterms(Mj) | Maxterms |
| 0 | 0 | 0 | M0 | x+y+z |
| 0 | 0 | 1 | M1 | x+y+z’ |
| 0 | 1 | 0 | M2 | x+y’+z |
| 0 | 1 | 1 | M3 | x+y’+z’ |
| 1 | 0 | 0 | M4 | x’+y+z |
| 1 | 0 | 1 | M5 | x’+y+z’ |
| 1 | 1 | 0 | M6 | x’+y’+z |
| 1 | 1 | 1 | M7 | x’+y’+z’ |
what is the Canonical form representation of Boolean function?
How to determine the minterm representation of a function from truth table?
The simple way is to note down all the minterms from the truth table where function value is equal to 1. So just consider the following example
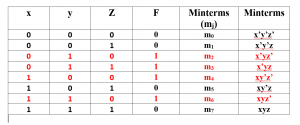
Here function can be written as summation of minterms where its value is equal to 1.
F(x,y,z)=x’yz’+x’yz+xy’z’+xyz’
Another notation that is used for representation of function as summation of minterms is to write down the summation sign and then include the subscripts of miterms involved.
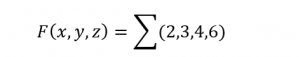
How to determine the maxterm representation of a function from truth table?
Since 1 represents the function F in the table, so 0 represents complement of the function. If we do write those minterms and then take complement of this function, the original function is obtained. Lets just consider the previous example
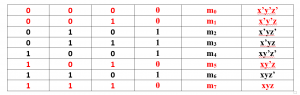
Now we can write it as
F'(x,y,z)=x’y’z’+x’y’z+xy’z+xyz
Now lets just take its complement again for getting the original function
(F’)'(x,y,z)=(x’y’z’+x’y’z+xy’z+xyz)
According to DE Morgan’s Theorem
F(x,y,z)=(x’y’z’+x’y’z+xy’z+xyz)’
F(x,y,z)=(x+y+z)(x+y+z’)(x’+y+z’)(x’+y’+z’)
If you math these values with table you will get
F(x.y.z)=M0M1M5M7
which can also be written as
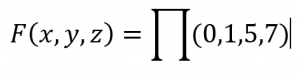
How to convert a Boolean function into its canonical form?
Since canonical form requires that all literals must be present in each term of the function. So we will try to complete them using different postulates of Boolean algebra.
Let us consider the following Boolean Function
F=A’+BC
Represent F=A’+BC as a summation of minterms
There are two ways to represent the given Boolean function as a summation of minterms. First one is to generate the truth table using the given Bollean expression and then use same method as mentioned previously.
So for F=A’+BC the truth table is determined as
| A | B | C | F=A’+BC | Minterms (mj) | Minterms |
| 0 | 0 | 0 | 1 | m0 | A’B’C’ |
| 0 | 0 | 1 | 1 | m1 | A’B’C |
| 0 | 1 | 0 | 1 | m2 | A’BC’ |
| 0 | 1 | 1 | 1 | m3 | A’BC |
| 1 | 0 | 0 | 0 | m4 | AB’C’ |
| 1 | 0 | 1 | 0 | m5 | AB’C |
| 1 | 1 | 0 | 0 | m6 | ABC’ |
| 1 | 1 | 1 | 1 | m7 | ABC |
now write down all those minterms where function is producing 1.
F(A,B,C)= A’B’C’+ A’B’C+ A’BC’+A’BC+ABC
F(A,B,C)=m0+m1+m2+m3+m7
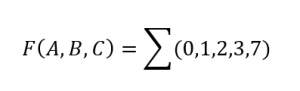
Another approach is to complete all literals by juts multiplying each terms with the summation of variable and its complement since (x+x’=1) which does not change the binary logic of Boolean function
so for F=A’+BC
lets consider the first term
A’=A'(B+B’)=A’B+A’B’
=(A’B+A’B’)(C+C’)=A’BC+A’BC’+A’B’C+A’B’C’
now consider the second term
BC=BC(A+A’)
=ABC+A’BC
now write down the resultant of both terms
F=A’+BC=A’BC+A’BC’+A’B’C+A’B’C’+ABC+A’BC
if any of the terms is repeated then write it only once. In this way you will get your result.
F(A,B,C)= A’B’C’+ A’B’C+ A’BC’+A’BC+ABC
F(A,B,C)=m0+m1+m2+m3+m7
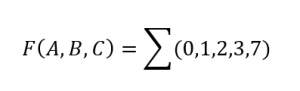
The maxterm representation can be directly derived from all the missing terms of minterm representation
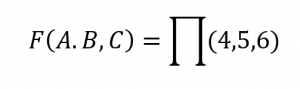
another way to convert the given Boolean expression in terms of maxterms is to first write it as a product of sums using distributive law and then complete the missing term by adding the multiple of a variable and its prime x.x’=0 since adding 0 will not change the actual logic.
F=A’+BC
F=(A’+B)(A’+C)
(A’+B)=(A’+B+CC’)=(A’+B+C)(A’+B+C’)
similarly
(A’+C)=(A’+BB’+C)=(A’+B+C)(A’+B’+C)
now writing both terms
F=(A’+B)(A’+C)=(A’+B+C’)(A’+B+C)(A’+B+C)(A’+B’+C)
since (A’+B+C) is repeated so it will be written only once
F=A’+BC=(A’+B+C’)(A’+B+C)(A’+B’+C)
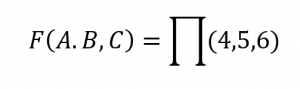
For video lecture, watch here
https://www.youtube.com/watch?v=QglupPfCCsI
Also read here
https://eevibes.com/computing/introduction-to-computing/what-are-number-systems/