
The Field of a Static Charge
Discuss the Field of a Static and a Moving Charge. For a single charged particle such as an electron, the electric field forms a single radian pattern as shown in the figure below. By convention, the field lines point outward for a positive charge (+Q) and inward for a negative charge (-Q). Field lines do not exist physically and they are drawn considering a positive test charge (Qt) is brought in the vicinity of these charges. This filed remains the same overtime, hence it is called a static field. The field stores the electromagnetic energy of the particle.
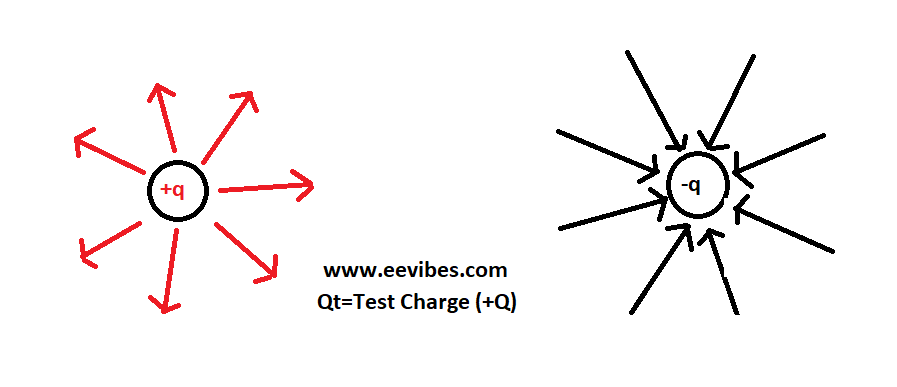
When another charge is present, the filed exerts a force on the other object and hence we say that energy is transmitted. When no other charged particles are present, the field has no effect but to store energy. The fact that the energy is transferred from the field only when another charged particle is present is a defining characteristics of the static field.
The Field of a Moving Charge
Now consider a same charged particle moving at a constant velocity, much lower than the speed of light. The particle carries the filed wherever it goes and at any instant the field appears the same as static field shown below.
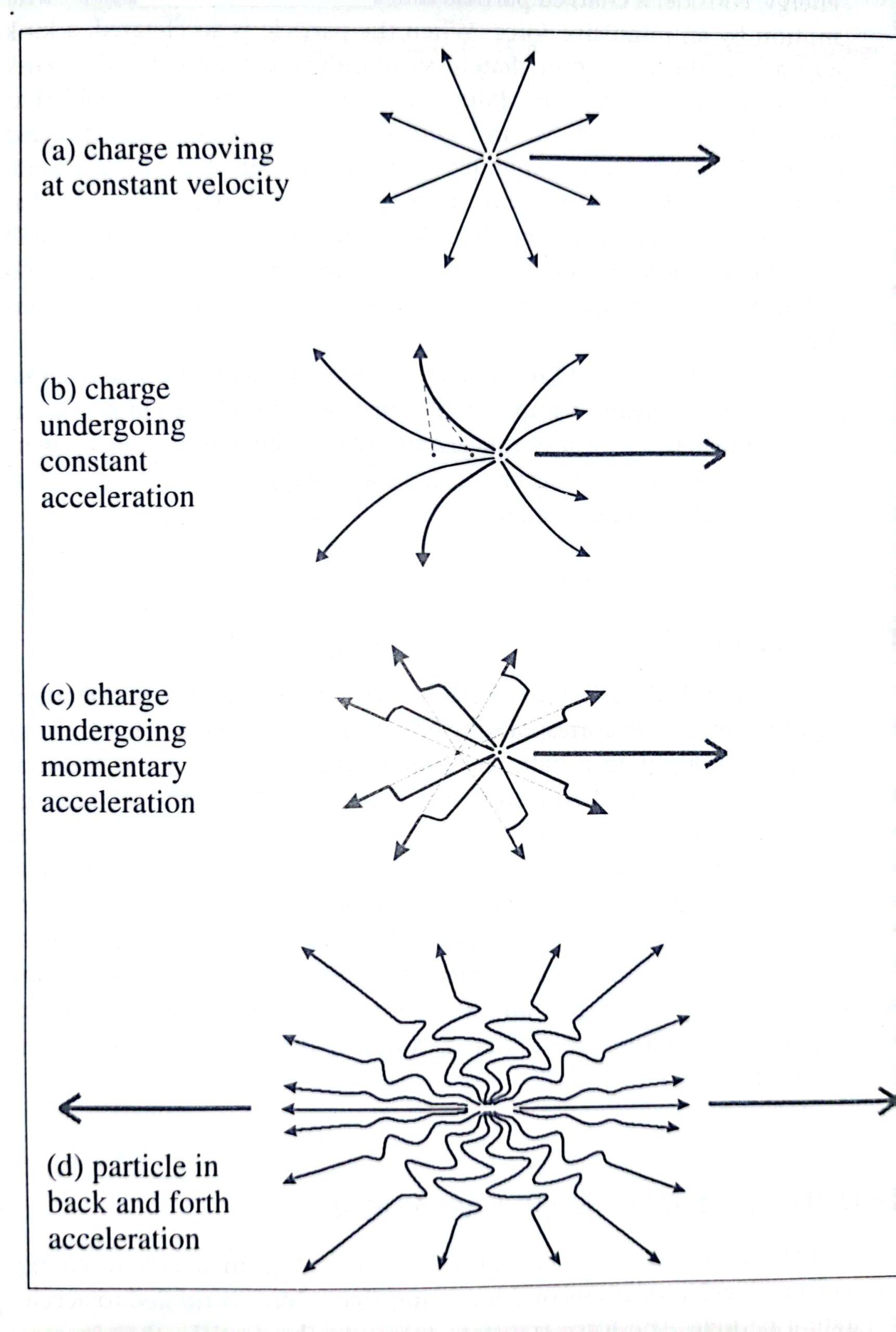
In addition, because the charge is moving now, a magnetic field also surrounds the charge in a cylindrical manner as governed by Biot-Savart law. As in the case of a static charge, both the electric and magnetic filed of a constant velocity charge serves to store energy and transmit the electric and magnetic forces only when other charges are present.
The Field of an Accelerating Charge
When a charged particle is accelerated, a very interesting phenomenon occurs. The lines of an electric filed start to look bent as shown in the above figure (b). A Review of Einstein’s theory of relativity helps to explain why this bending occurs. No particle, energy, or information can travel faster than the speed of light, c. This speed limit holds for fields as well as for particles. (For that matter, quantum electrodynamics says that a field is just a group of virtual particles called “virtual protons”.
For instance, if a charged particle were suddenly created, its field would not instantly appear everywhere. On the contrary, the field would first appear in the immediate region surrounding the particle and then extend outward at the speed of light. For example light takes around eight minutes to travel from sun to the earth. If the sun were to suddenly extinguish, we would we would not know until eight minutes later. Similarly, as a particle moves, the surrounding field continuously updates to its new position, but this information can propagate only at the speed of light.
What is the time retardation?
Points in the space surrounding the particles actually experience the field corresponding to where a particle was at a previous time. This delay is referred to as time retardation.
It seems reasonable to assume that even a charge moving at constant velocity should cause the field lines to bend due to this time retardation. However, Einstein’s theory of relativity states that velocity is a relative measurement, not an absolute measurement. If the field lines are straight in one inertial observer’s reference frame, they must be straight in all other inertial observer’s reference frames.
Why Bent Field Lines of a Charge Correspond to Radiated Energy?
To understand why bent field lines of a charge correspond to radiated energy, consider a charged particle that starts at rest and is kicked into motion by an impulsive force. When the particle is accelerated, a kink appears in the field immediately surrounds the particle. This kink propagates away from the charge, updating the rest of the field that has lagged behind as shown in above figure (c). Part of the energy expended by the driving force is expended to propagate the kink in the field.
Therefore, the kink carries with it energy that is electromagnetic radiation. Fourier analysis shows that since the kink is a transient, it will consist of a superposition of many frequencies. Therefore a charge accelerated in this manner will radiate energy at many simultaneous frequencies.
Keep in mind here that this is a field of an individual charge. It does not mean to imply that bent field lines always imply radiation. The following figure shows an example of two charges producing bent field lines. No radiation occurs in this static setup. It is the acceleration that produces the radiation.

Relativistic Effects:
For charges moving at speeds close to the speed of light, relativistic effects become important. These effects necessitate the use of the Lorentz transformation to account for the contraction of length and the dilation of time experienced by the moving charge [Einstein, A. (1905). On the electrodynamics of moving bodies].
Advanced Literature:
- For a deeper understanding of the electric field of moving charges, advanced texts like Griffiths’ Introduction to Electrodynamics or Jackson’s Classical Electrodynamics delve into special relativity and explore topics like the Biot-Savart Law for calculating the magnetic field of a moving current.
Additional Considerations:
- The literature review can be further tailored to specific applications of moving charges, such as charged particle beams or current-carrying conductors.
- Modern research explores the electric field of moving charges in complex systems like plasmas and semiconductors, utilizing computational techniques.
This review provides a starting point for exploring the electric field of static and moving charges. By delving deeper into the references mentioned and exploring more advanced resources, you can gain a comprehensive understanding of this crucial concept in electromagnetism.