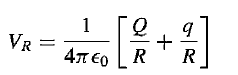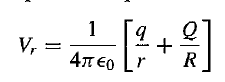Table of Contents
Electrostatic Generator
What is the Electrostatic Generator? An electrostatic generator is also called the van de Graaff generator as it was put in practice by Van de Graaff and conceived by Lord Kelvin. It consists of a hollow spherical conductor supported on an insulated hollow column as shown in the following figure:
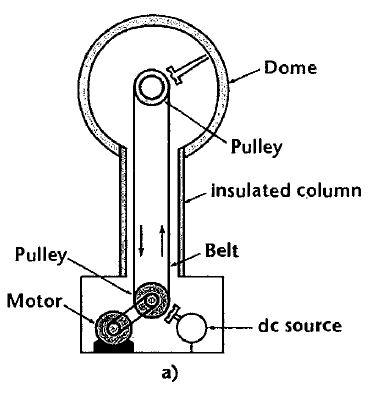
A belt passes over the pulleys. The lower Pulley is driven by the motor, and an upper is an idler. A number of sharp points projecting from a rod are maintained at a very high positive potential, and the air around the points becomes ionized.
The positive ions are repelled from the sharp points and some of these ions attach themselves to the surface of the moving belt. A similar process takes place at the metal brush inside the dome. As the charge builds up, the potential of the dome rises.
With the Van de Graaff generator a potential difference as high as several million volts can be realized. Its chief application is to accelerate the charged particles to acquire high kinetic energies, which are then used in atom smashing experiments.
Basic Operation of Generator
In order to understand the basic principle of operation, consider a hollow, uncharged, conducting sphere (dome) with a small opening as shown below:
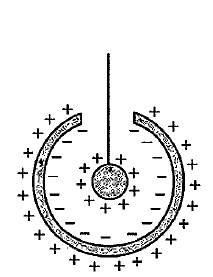
Let us now introduce a positively charged small sphere with the charge q through the opening into the cavity. As soon as equilibrium state is reached, the inner surface of the dome acquires the net negative charge, while the positive charge q is induced on its outer surface.
If the small sphere is now made to touch the inner surface of the doom, the positive charge of the small sphere will be completely neutralized by the negative charge on the inner surface of the dome.
However, the outer surface will still maintain the positive charge q. If the small sphere is now withdrawn, charged again to q, and reinserted into the dome, the inner surface will again acquire the negative charge, causing the charge on the outer surface to increase by the same amount.
By touching the small sphere to the inner surface of the dome, and the small sphere are again free of charge. But there is now twice as much charge on the outer surface of the dome.
In other words, by bringing in a charged body and touching it to the inner surface of the dome, all the charge on the charged body can be transferred to the outer surface of the doom. This process is obviously independent of the initial charge on the outer surface of the dome.
Let us suppose that at any instant, after the equilibrium state has been arrived, the charge on the smaller sphere inside the dome is q and that on the outer surface of the dome is Q. If radii of the inner and outer surfaces are r and R respectively, the potential at any point on the dome is given as:
The first term inside the bracket is the contribution to the potential on the dome by its own charge Q, and the second item is due to the equilibrium surface at a radius R created by the charge q on the small sphere. The potential on the small sphere is
where the first term is due to the charge on the small sphere and the second term takes into account that the small sphere is inside the large sphere.
Thus the potential difference between the spheres is
For s positive charge q the potential of the inner sphere will always ne higher than that of the dome. If the two spheres are electrically connected, the entire charge on the inner sphere will flow towards the outer surface of the dome regardless of the charge Q on it.
This is another way that we can explain the charge transfer from the inner sphere to the outer surface of the dome. Note that the potential difference is zero only if q=0.
Applications of Electrostatic Generator
Electrostatic generators, which produce high-voltage electricity through the build-up and discharge of static electricity, have various applications across different fields. Here are some common applications:
Research and Education:
Electrostatic generators are often used in laboratories and educational institutions to demonstrate principles of electricity, electrostatics, and high voltage phenomena. They serve as valuable teaching tools for students learning about electromagnetism.
Particle Accelerators:
Electrostatic generators are integral components of particle accelerators used in physics research. They generate the high voltages needed to accelerate charged particles to high speeds for experiments in nuclear and particle physics.
X-ray Machines:
Electrostatic generators are used in some types of X-ray machines to produce the high voltages required to accelerate electrons, which then collide with a target material to produce X-rays used for medical imaging and industrial inspection.
Electrostatic Painting:
Electrostatic generators are employed in electrostatic painting systems. These systems charge paint particles with static electricity, creating an attractive force between the charged particles and the object being painted. This results in a more uniform and efficient coating application compared to traditional painting methods.
Air Purification:
Electrostatic generators are utilized in electrostatic precipitators (ESP) for air purification systems. ESPs charge particles in a gas stream with static electricity, causing them to adhere to collector plates or other surfaces. This process removes pollutants such as dust, smoke, and particulate matter from the air.
Photocopiers and Laser Printers:
Electrostatic generators are employed in photocopiers and laser printers to create electrostatic charges on photoreceptors or drums. These charged areas attract toner particles, which are then transferred onto paper to produce printed documents.
Van de Graaff Generators:
Van de Graaff generators, a type of electrostatic generator, are commonly used in physics demonstrations and experiments. They generate high voltages using a moving belt to accumulate static electricity, producing impressive electrical arcs and sparks.
Nuclear Fusion Research:
In some experimental setups for nuclear fusion research, electrostatic generators are used to create the high voltages needed to initiate and control fusion reactions.
Electrostatic Precipitation in Industry:
Many industries use electrostatic precipitation to remove particulate matter from exhaust gases, such as those produced by power plants and industrial facilities. This helps to reduce air pollution and meet environmental regulations.
Electrostatic Motors: Although less common than electromagnetic motors, electrostatic motors have been developed and used in certain niche applications. These motors utilize the forces generated by electrostatic charges to produce motion without the need for traditional electromagnetic components.
Also read here: