Table of Contents

Introduction to even and odd functions

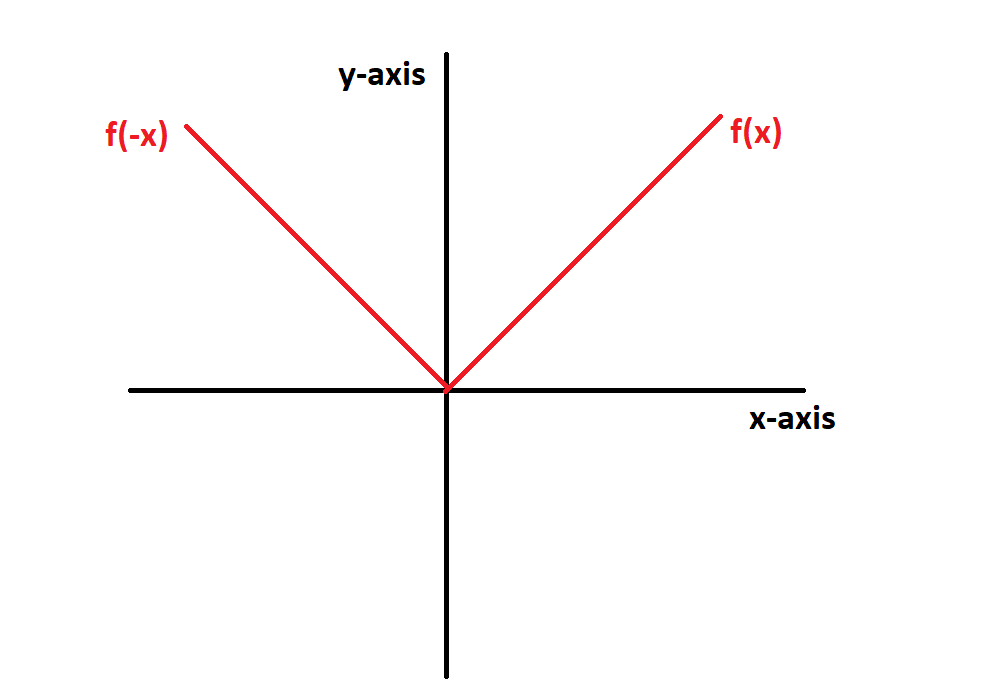
In this article you will learn about what are the even and odd functions? In this article we have described with examples to identify either a given function is even or odd. Any function whose graph is symmetrical around the y-axis is called an even function. Mathematically, if we have y=f(x)=f(-x) for any value of x then we say that this is an even function. The graph of y=|x| is shown below which shows the behavior of function is same for all values of x.

even function graph — Graph of an even function

What are the even functions?

All the functions that have even and positive power of x are even functions. For example

X², X⁴, X⁶,…….. Xⁿ

Because when we look at the graphs of such functions they show the reflection around the y-axis. y=cos(x) is also an even function.

Some functions like (x+1)^2 are not even functions. All functions of constants (whose degree is zero) are called even functions generally.

What are the odd Functions?

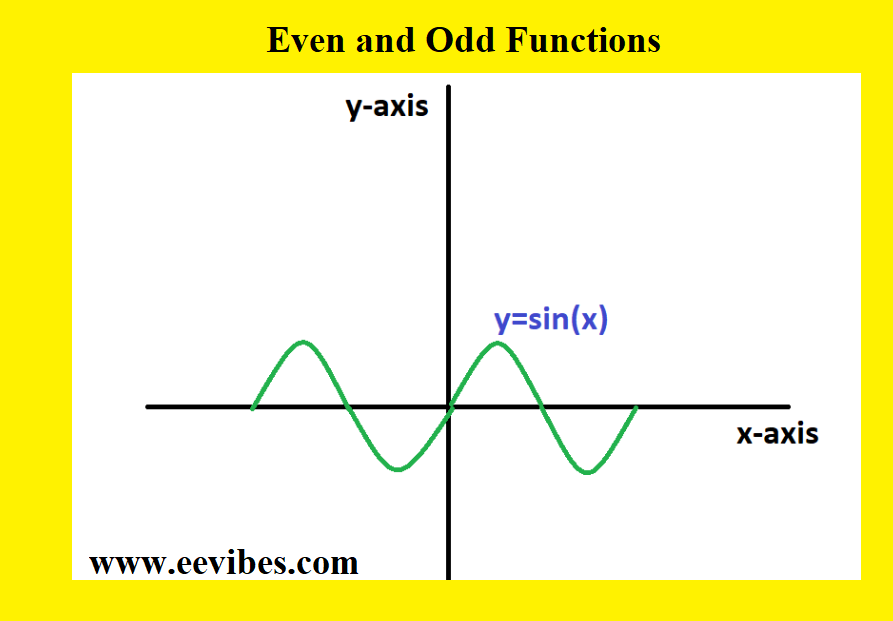
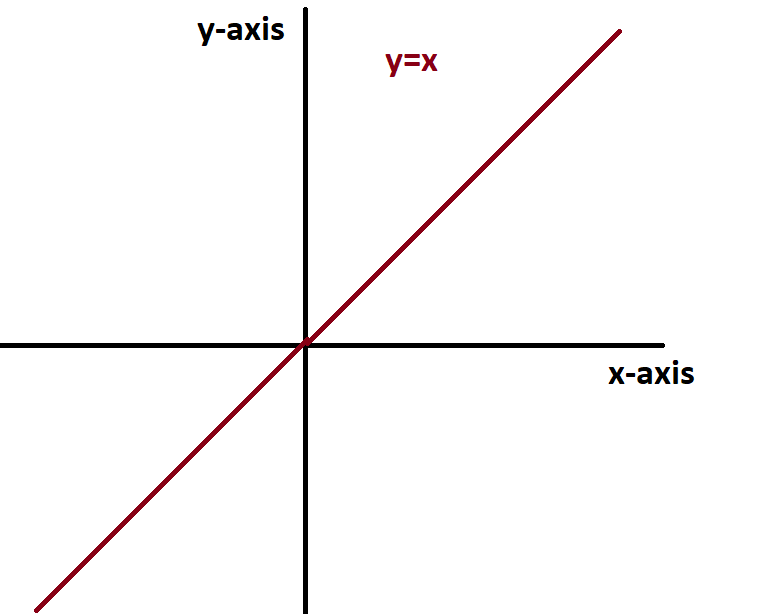
A function is odd if f(-x)=-f(x). It means if the rotation through half turn leaves a function unchanged, then it is called an odd function. Odd functions reverse their sign if they are reflected around the y-axis. The function y=x and y=x^3 are the examples of odd functions.

odd function example — odd function graph

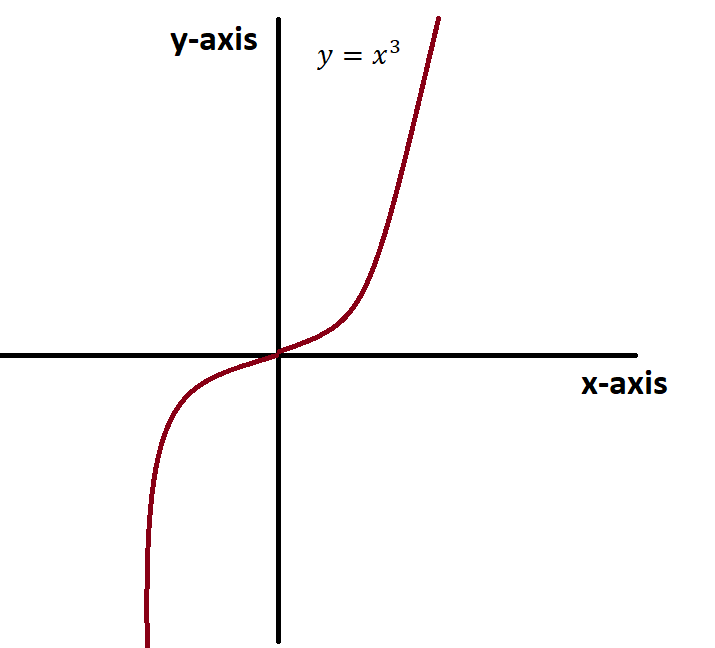
odd function's another example — odd function graph

Similarly, the graph of a sinusoid is also an example of odd function because it does not give symmetry around y-axis.

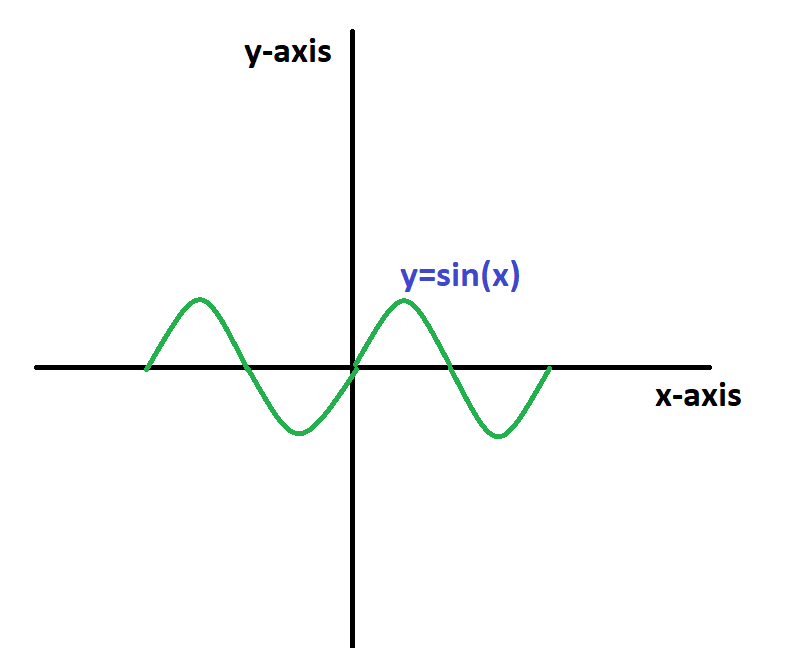
sinusoidal function is an odd function — Sin(x)

Neither even nor Odd functions

There are some functions that are neither even nor odd. Even and odd is just a term and all of the functions are not supposed to be classified amongst these two categories. For example, . Polynomials turn out to be neither even nor odd functions.

How to tell if a function is even or odd?

If we want to test the given expression of a function is even or odd, we will replace x by -x and then see either it becomes y(x)=y(-x) or y(-x)= -y(x).

Example:

Even Function Test

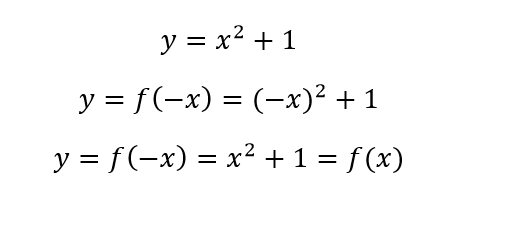
Odd Function Test

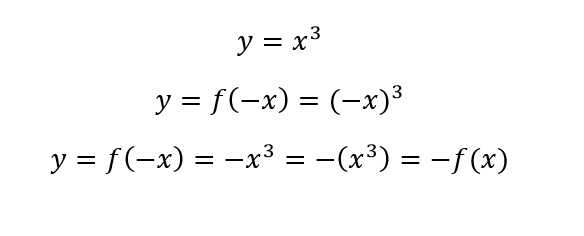
Neither even nor odd

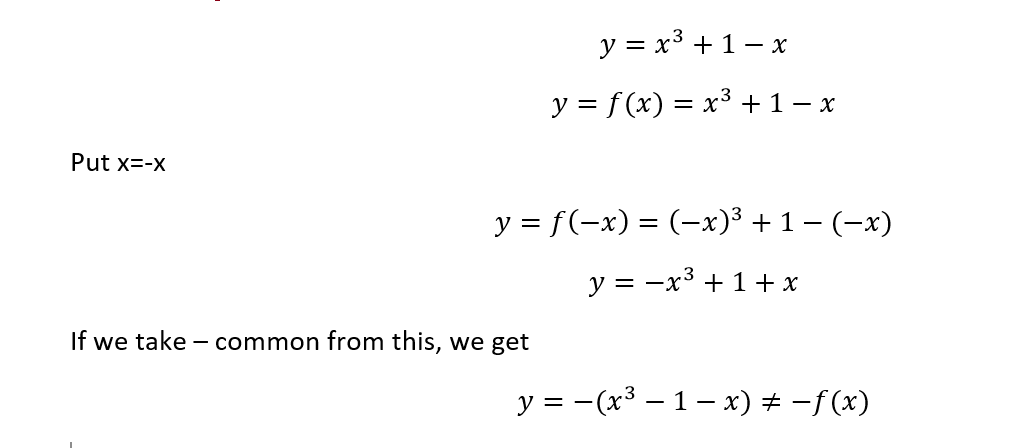
More examples to tell if a function is even or odd

examples of even and odd functions — Some examples for even odd functions test

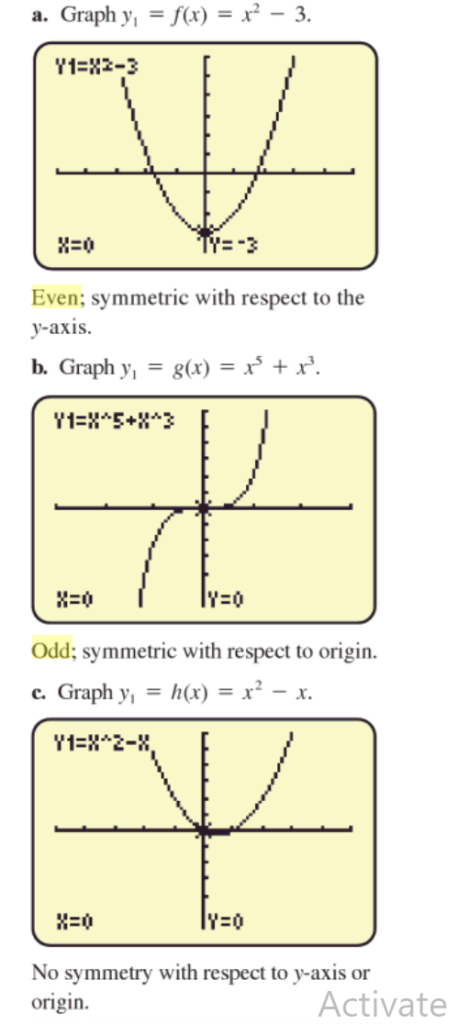
Graphical Depiction of even/odd functions

Here is the graphical depiction of even and odd functions.

even odd functions representation — graphical depiction of even odd functions

Properties of even/odd functions

The product of two even functions is an even function .
The product of two odd functions is an even function .
The product of an even and an odd function is an odd function .
The sum of two even functions is an even function.
The sum of two odd functions is an odd function.

Application of even and odd function

If a wavefunction of a particle is an even function (symmetric, centered at the origin), then the expected location of the particle (assuming it exists) is that the origin, because |ψ(x)|2|If a wavefunction of a particle is an even function (symmetric, centered at the origin).

Summary of How to tell if a capacity is even or odd?

Imagine a scenario where we’re given a capacity and we don’t know whether it either odd or even. That won’t be an issue! How about we use what we have realized so far to decide if a capacity is odd or even.

At the point when given the capacity: see what happens when we supplant x with – x.

When you plug in – x into f(x), did the capacity continue as before? Assuming this is the case, f(x) is even.

When you plug in – x into f(x), did the indication of capacity’s coefficient change? Provided that this is true, f(x) is odd.

At the point when given the diagram: decide if the chart is symmetric about the inception or y-pivot.

On the off chance that the diagram is symmetric about the y-hub, the capacity is even. How would we do this?

Envision collapsing the chart vertically and check whether the two diagrams would lie alongside one another.

You can likewise spot for numerous focuses and check whether x and – x offer a similar facilitate.

In the event that the diagram is symmetric about the inception, the capacity is odd. How would we do this?

Envision collapsing the diagram askew (check the two headings) and check whether the two charts would lie alongside one another.

You can likewise spot for different focuses and check whether x and – x offer the y-

Are there functions that are neither odd nor even?

Should all functions be either odd or even? No. There are examples where a capacity neither meets the meaning of even and odd functions. The capacity f(x) = (x + 1)2 is an illustration of a capacity that is neither odd nor even.

What are the even and odd functions: Examples