What is the inverse of a function?
How to determine the inverse of a function give an example? As we know that the function can be represented either as an “expression” or in the form of tabular data. That tabular data must be of the form of set of ordered pairs. For example {(1,1), (2,4), (3,9),(4,16)……..}. If you closely look at the behavior of these data points they represent the square function y=x2. It is to be noted that the first value corresponds to the independent variable ‘x’ and the second value corresponds to the dependent variable ‘y’. So these ordered pairs are actually written as (x,y)={{(1,1), (2,4), (3,9),(4,16)……..}. Now what happens if we switch the position of x and y in this expression? How can we find the inverse of a function?
When we write as (y,x)={(1,1),(4,2),(9,3),(16,4)……} then we say this as inverse of the function. The inverse of the function is obtained by switching the position of x and y in the set of ordered pairs of a function.
Representation of inverse of a function
The inverse of the function f is represented as f-1. The inverse of the function can be or can not be a function. The inverse of the function y=mx+c can be written as x=my+c. From this it can be said that the inverse of a line is a line. Also the straight line equation having zero y-intercept and starting from the origin has the equation as {(x,y)|y=x} is an example of self inverse. This function is also known as the identity function.
important note:
It should be noted that y=√x where x is a positive number represents a function. But the expression y2=x is not a function. Why? Because when you take under root on both sides of this equation you will get y=±√x which fails the definition of a function.
The function and its inverse follows the following rule.
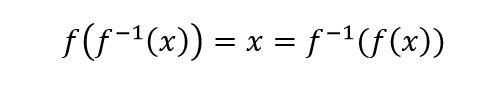
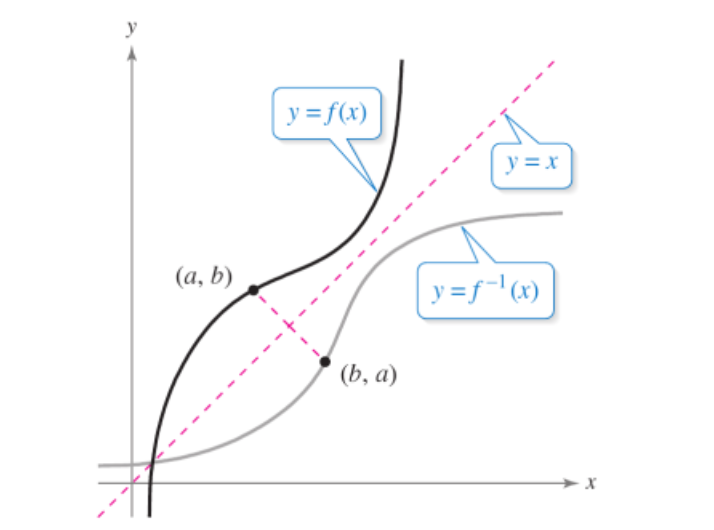
Graph of the function and its inverse
The function and its inverse can be plotted as shown below
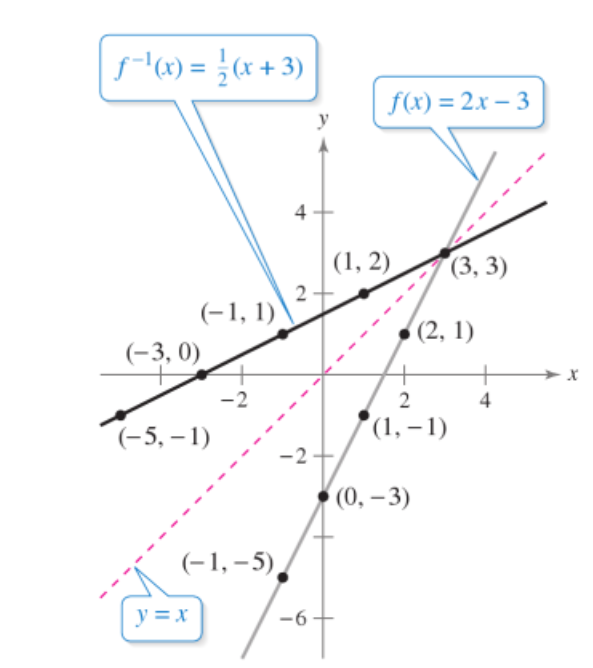
How to find the inverse of a function with examples.

How to find the inverse of a function?
Question
Find the inverse of the following functions.
(x,y)={(2,1),(3,2),(4,3),(5,4),(6,5)}
Solution:
Question
(y,x)={(1,2),(3,2),(3,4),(4,5),(5,6)}
{(x,y)| y=4x+7 x belongs to R}
Solution:
This is a linear function and its inverse is {(y,x)| x=4y+7 y belongs to R}. When we draw the graph of function and its inverse in this case we will get the symmetry with respect to the line y=x.

Also read here:
https://eevibes.com/mathematics/elementary-math/how-to-test-if-a-function-is-even-or-odd/