Introduction to open bracket methods
what are the open bracketing methods in numerical analysis? Bracketing methods are those methods which continue to converge as your algorithm proceeds. We always need an initial guess while applying the bracketing methods such as the bisection method or regula falsi method. In contrast to bracketing methods there are open bracketing methods available that may or may not converge as the algorithm continues. But the plus point is open bracketing methods are fast enough as compared to bracketing methods. The initial guesses are not supposed to bracket the root of the equation.
comparison of open bracket and bracketing method
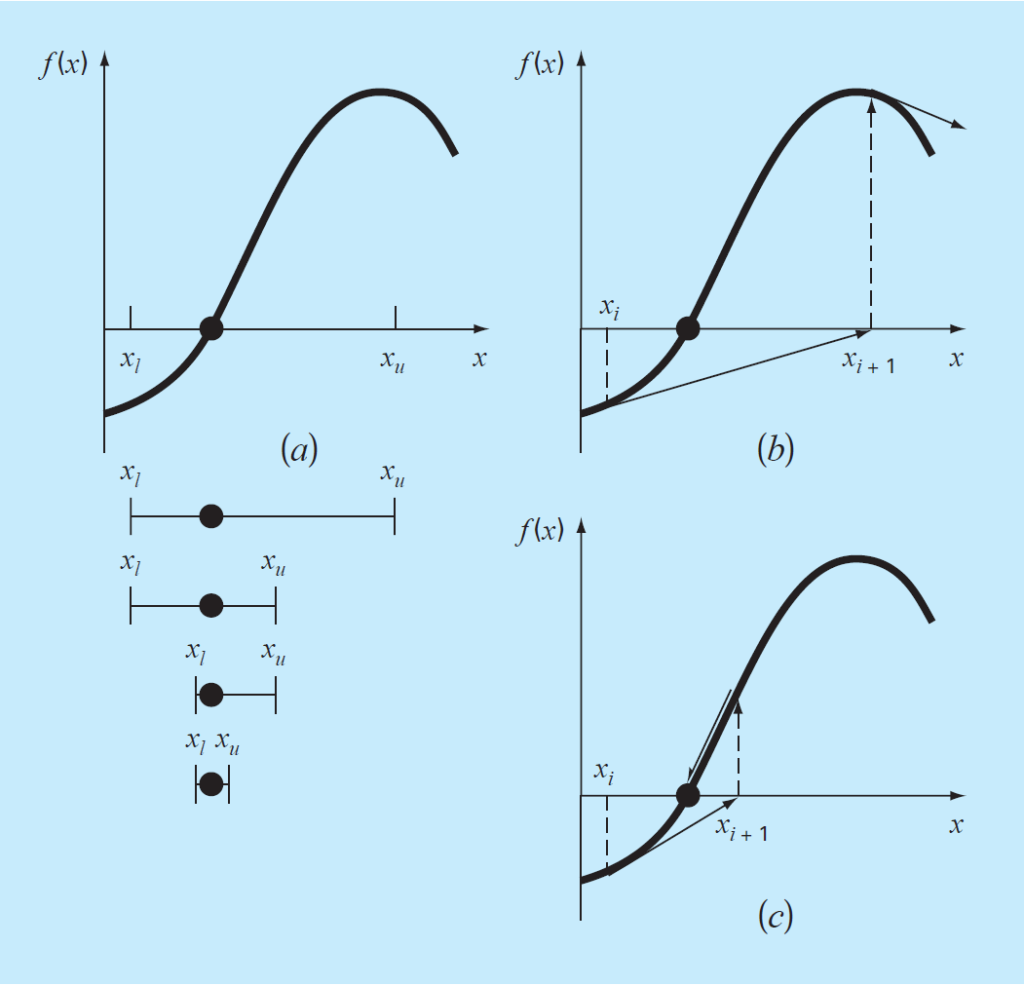
The following figure shows a comparison between bracketing and open bracket method. The bracketing method in figure (a) is the bisection method where the multiple iterations are required for determining the root of the function f(x). So bracketing methods always converges to the root. While figure (b) shows the open bracketing method diverging from the actual root of the equation. But in figure (c) part it is clearly shown how a single iteration converges to the root. So it can be concluded that whenever the open bracketing methods converge, they converge faster. How to use open bracketing methods for finding roots of equation?
Types of open bracket methods
There are different types of open bracketing methods that are
Fixed point method
In this method the formula is developed from the function f(x)=0 such that we have
x=g(x).
Then the consecutive iterations are employed on this formula for approximating the root of the equation. The transformation of the form of x=g(x) can be developed either by arranging the actual equation or by adding x on both sides of the equation. For example
![]()
can be rearranged as
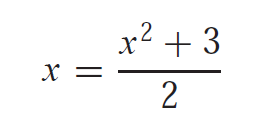
or simply sin(x)=0 can be formed as x+sin(x)=x
The iterative formula is then developed as
![]()
And the approximated error associated can be calculated as
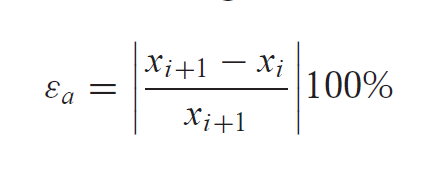
Example
Use the fixed point method for finding the root of the equation f(x)=x-e^-x
Solution
The above equation can be written as
x=e^-x
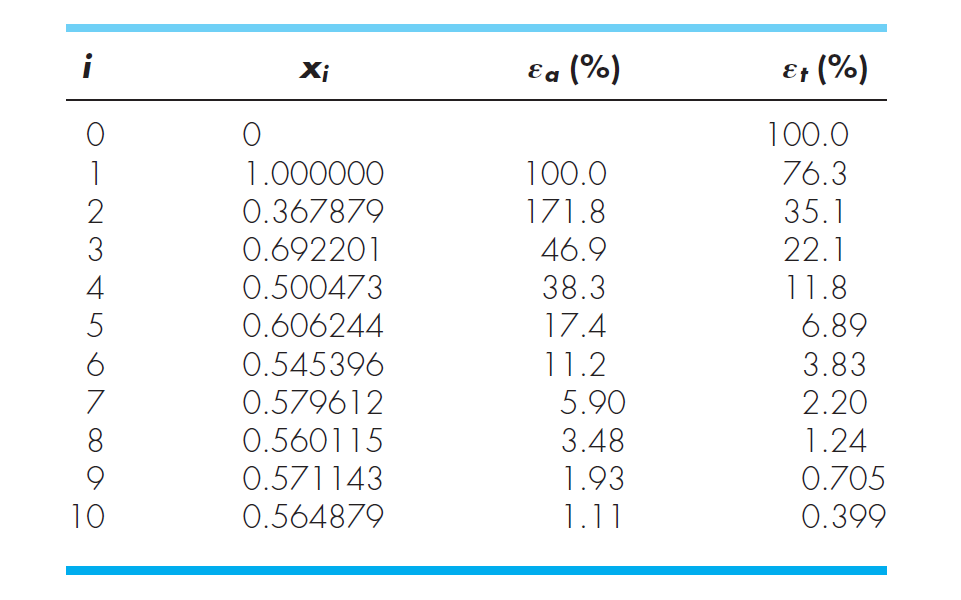
Assuming x=0 as initial guess the algorithm will proceed like shown below. The true value of the root is 0.56714329
Convergence criteria for fixed point method
The expression x=g(x) that we develop from f(x)=0 should be such that the method should always converge. Since there can be many possibilities of getting the form of x=g(x) from the same function. Just like in above case where another form of the equation could have been different (determine it!).
So the question is which form of x=g(x) should be used. The answer is if the derivative of g(x) is less than 1, then that form of g(x) will give us convergence. So I hope the answer is cleared to what are the open bracket methods for finding roots of equation?
Also read here
https://eevibes.com/what-is-the-bisection-method/