What is the bisection method?
What is the bisection method? Example of Bisection method. The bisection method is used for finding the roots of transcendental equations or algebraic equations. This is also called a bracketing method as its brackets the root within the interval. The selection of the interval must be such that the function changes its sign at the end points of the interval. This method is basically used for solving the equations of the form of f(x)=0. This is actually a graphical method where the graph of the function is drawn and we notice where the function cuts the x -axis. This point is called the root of the equation then.
Graphical methods gives us an approximation of the roots plus also some very useful information that can help us for finding the number of roots.
If both the upper and lower point gives the positive value of the function, then either the function has no root or even number of roots. If the functions has opposite signs at the end points of the interval then there will be odd number of roots as shown in the figure below.
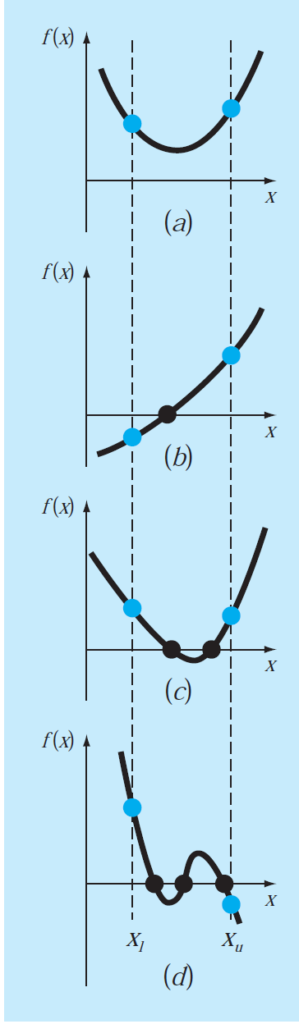
When the function is tangent to x-axis then multiple roots exist. In that case the function may be changing its sig at the end points of the interval, there will be even number of roots as depicted in the following figure
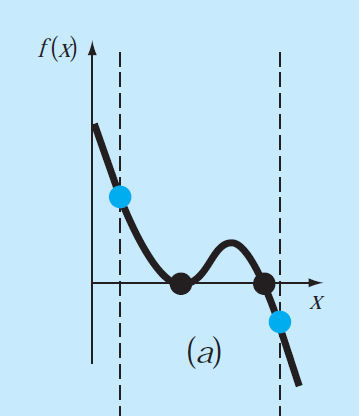
Explanation
In general if f(x) is a continuous function between an interval having end point as [ xL xU] and function has opposite sign at these points such that
f(xL ).f(xU)<0
then there must be some root/roots between this interval. The other names of the bisection method are interval halving interval chopping or Bolzano method. In this method the interval is divided into half based on the above mentioned criteria f(xL ).f(xU)<0. Then we try to locate the root.
Steps of how Bisection method works

Termination criteria for Bisection method
The method could be kept on getting a refined gauge of the root. We should now build up a target standard for choosing when to end the method. An underlying proposal may be to end the count when the genuine blunder falls beneath some prespecified level. We may conclude that we ought to end at the point when the mistake dips under, say, 0.1 percent. This procedure is imperfect in light of the fact that the blunder gauges in the model depended on information on the genuine foundation of the capacity. This would not be the situation in a genuine circumstance on the grounds that there would be no reason for utilizing the method in the event that we definitely knew the root. In this manner, we require a mistake gauge that isn’t dependent upon prescience of the root. The approximated relative percentage error is given as
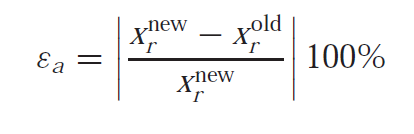
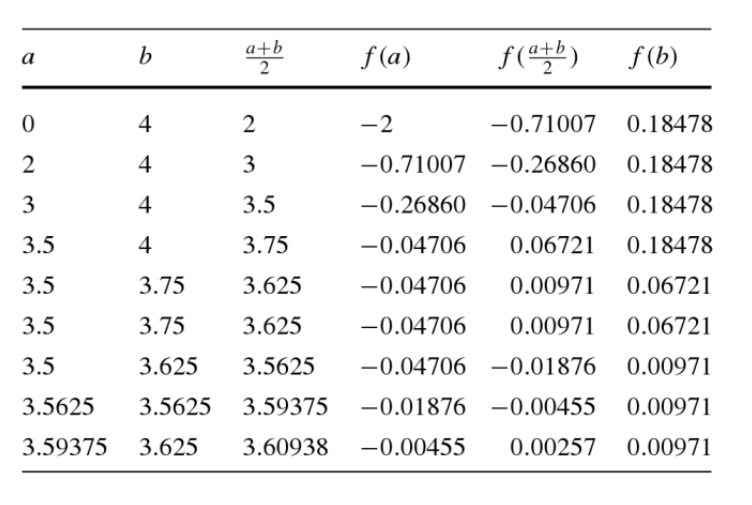
Example of Bisection Method

code for bisection method

Bisection Method video explanation
Comparison of bisection method with false position method
https://www.youtube.com/watch?v=QXy_soGFi5Y
Also read here
https://eevibes.com/what-is-the-meaning-of-interpolation-what-are-the-types-of-interpolation/