Introduction to fixed-point-method
How to find the convergence of fixed point method. One of the numerical methods for solving transcendental equations or algebraic equations is fixed-point (FP) method. This falls in the category of open bracketing methods. Open bracketing methods are those that start with one initial guess or two initial guesses but do not bound root of equation within the selected interval.
It may be the case when these methods do not converge to the root but when they converge, they converge very fast as compared to the bracketing methods.
Versions of open-bracket methods
- Fixed-Point (FP)/method of successive approximations
- Newton Raphson method
- Secant method
FP or Method of successive approximations
Another name for fixed point method is “method of successive approximations as it successively approximates the root using the same formula. In this method we will be solving the equations of the for of f(x)=0. The first step is to transform the the function f(x)=0 into the form of x=g(x) such that x is on the left hand side. This can be done by some simplifying an algebraic expression or by adding x on both sides of the equation. For example,

So it can be seen clearly that there are many forms of x=g(x) are possible. Now the question arises which one to select?. There is a convergence criteria that will determine or help us to decide which form of x=g(x) should be used. Once you select the form of x=g(x) the iterations for the FP method can be started like
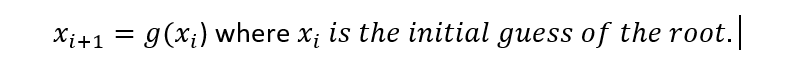
The formula for the relative error is given as:
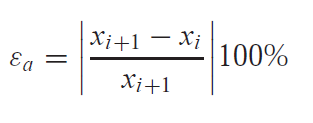
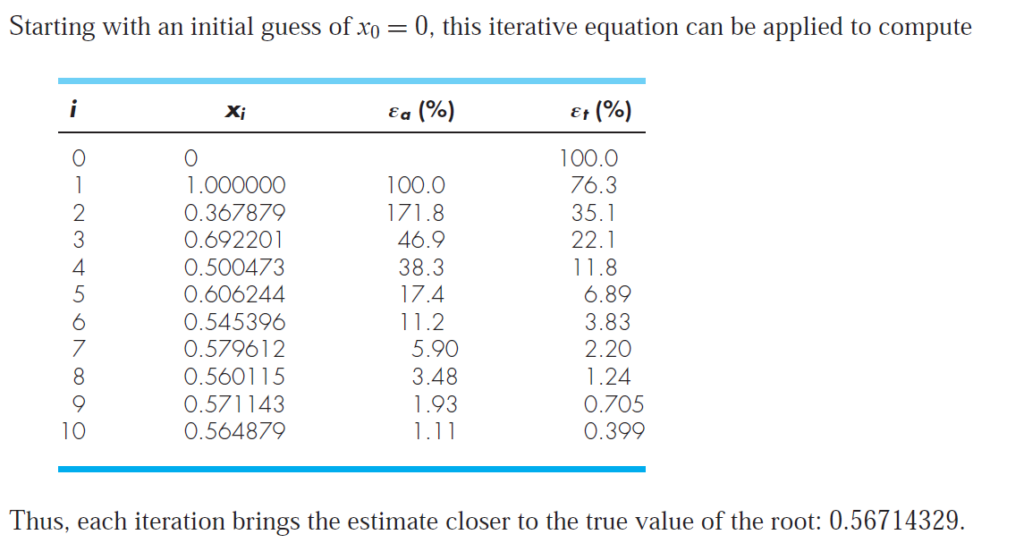
Example
Use simple FP iteration to locate the root of the equation f(x)=(e^x)-x with initial guess x1=0.
Graphical representation of root using fixed-point-method
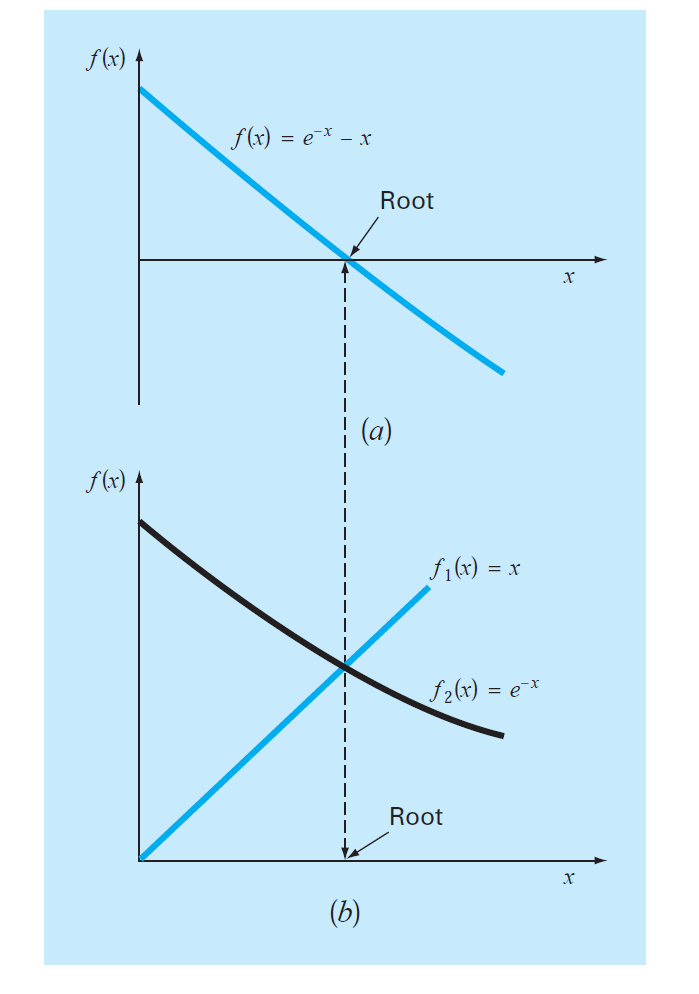
In the above figure part (b) the straight line represents y=x wherever this straight cuts the function g(x) will give us the solution of equation f(x)=
Convergence of fixed point method graphically
The convergence criteria of FP method states that if g'(x)<1 then that form of g(x) should be used. This will make sure that the slope of g(x) is less than the slope of straight line (which is equal to 1). If this condition does not fulfill, then the FP method may not converge.
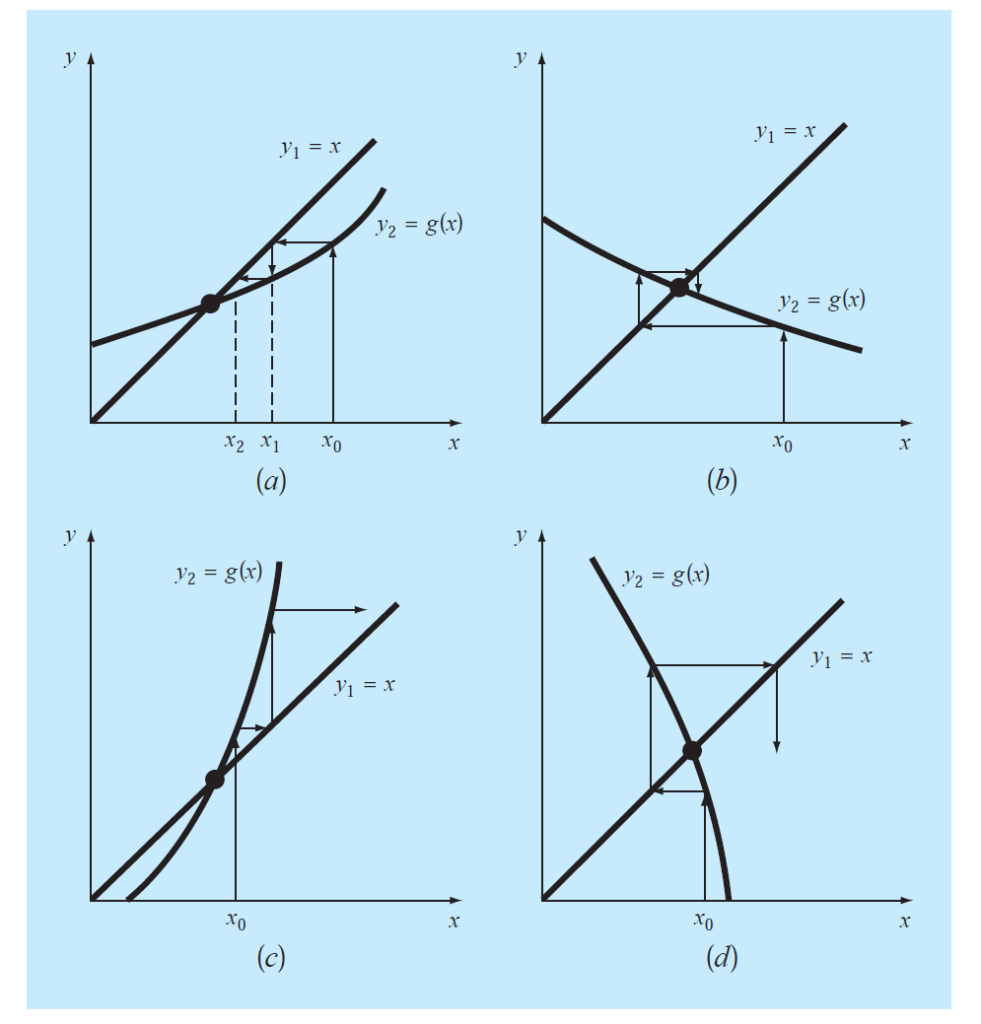
There are four cases discussed.
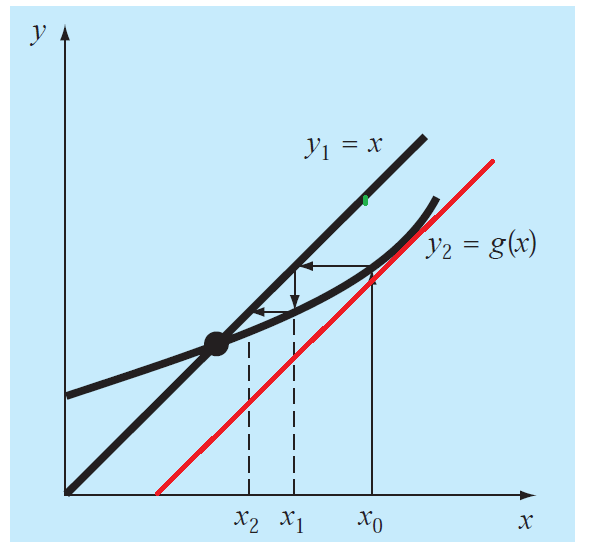
in above figure part (a) starting with initial guess x0, we calculated g(x0) and then this gives us x1,then this x1 is substituted in g(x) again to calculate x3 and so on. Since the slope of g(x) is less than the straight line so this form of g(x) converges.
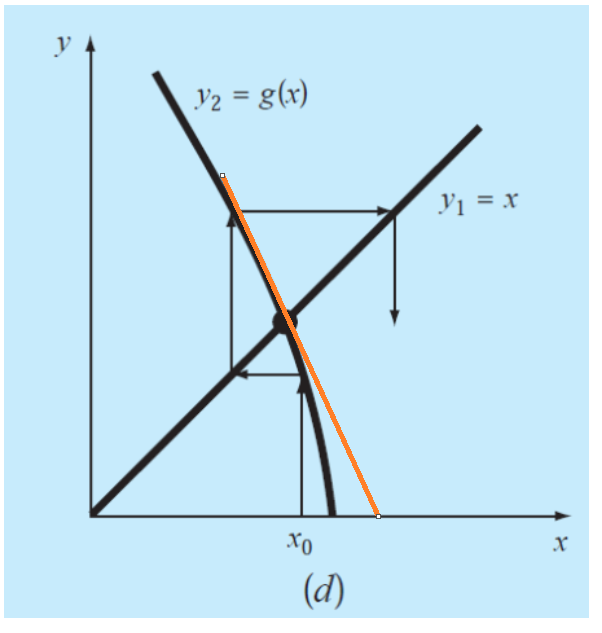
In the above case it can be seen the slope of g(x) is greater than 1 (the slope of straight line) so the initial guess diverges from the original root.
Also read here
Example of method of false position
Example of method of false position
Also read here