Table of Contents
Prove that Maclaurin series is the special case of Taylor’s series expansion.
Prove that the Maclaurin series is the special case of Taylor’s series expansion. Taylor’s series is used for finding the value of a function at point ‘x2’ given that you know the value of function and its derivatives at some point ‘x1’. Where x2-x1=h is the difference between two points.
The Taylor’s series is given as:

The first term in the series is called zero order approximation as it does not contain (or zero order derivative) in it. The second term is called first order approximation as there is first derivative present in the expression and so on. Taylor’s series gives the approximation of a function in the form of a polynomial. So, if are given the order of polynomial then the higher order derivatives will be zero and hence the Taylor’s series gives the exact solution or approximation of the function at any point.
Example of Taylor’s series

Derivation of Maclaurin series from Taylor’s series
Lets derive the Maclaurin series from the Taylor’s series with x1=0 and h=x
Put these values in the above formula
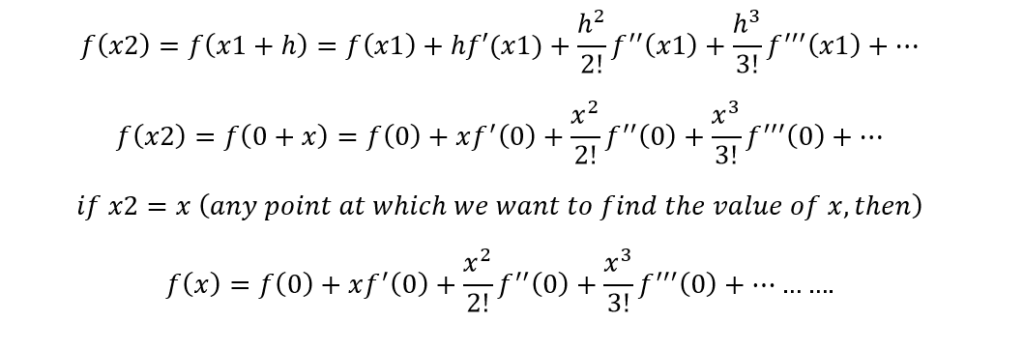
Also read here