Large numbers of you should be acquainted with the utilization of a connected rundown in reality and its significance. We utilize connected records to keep a registry of names, dynamic portion of memory, and make an execution of basics information structures like stacks and lines, and so forth?
Knowing this in this instructional exercise we will talk about the essential comprehension of a connected rundown, and execute and break down how to invert a connected rundown in C++. We should get Kraken!
What is Linked List?
The overall definition is that a connected rundown is a succession of information structures, the hubs are associated with pointers, and the last hub focuses on NULL.
A connected rundown is a succession of connections that contain components associated utilizing pointers. Each connection which is a pointer contains an association with another hub. The connected rundown is the second most used information structure later clusters.
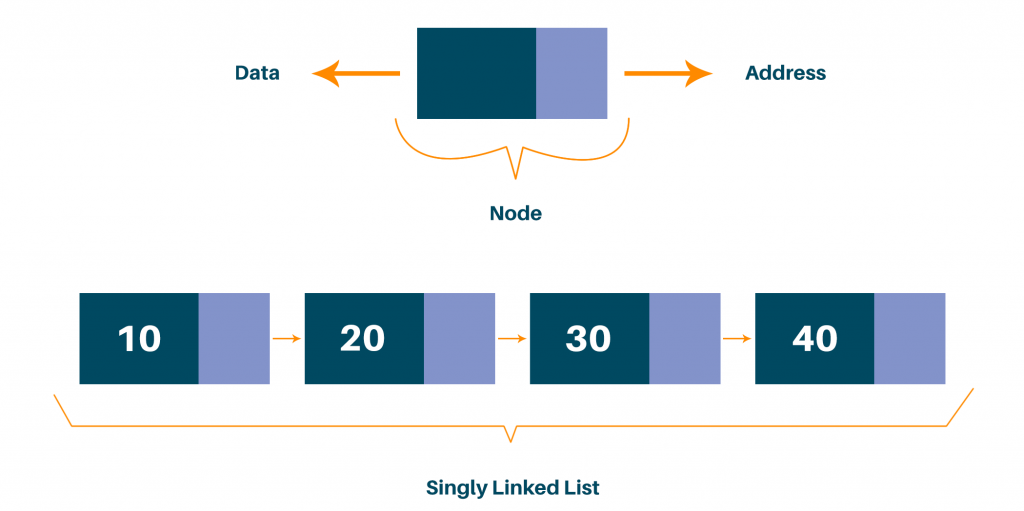
There are three parts of a connected rundown:
Hub − Each hub stores information which is called a component.
Next − Every hub of a connected rundown contains a connection to the following connection that is Next.
Head − A Linked List contains the pointer to the primary connection called a head pointer.
How might we do that?
Switching of a connected rundown implies that the head pointer will highlight the terminal hub of the connected rundown or the last hub of the connected rundown and the current head will point towards NULL.
This can be effectively finished with the assistance of three pointers where in with every crossing through the connected rundown they continue to switch the pointer to the following hub in the connected rundown.
What is connected rundown?
How to Reverse a Linked List?
Switching the rundown infers turning around every one of the components and we can do it by turning around every one of the connections and make the following pointer highlight the past hub.
Issue Description
In this issue proclamation we are given the pointer or reference to the top of a separately connected rundown, transform the rundown, and return the pointer or reference to the top of the new turned around connected rundown.
For instance, think about the accompanying connected rundown:

Connected rundown model
Subsequent to switching the total connected rundown we return the pointer to the new connected rundown as exhibited in the figure:
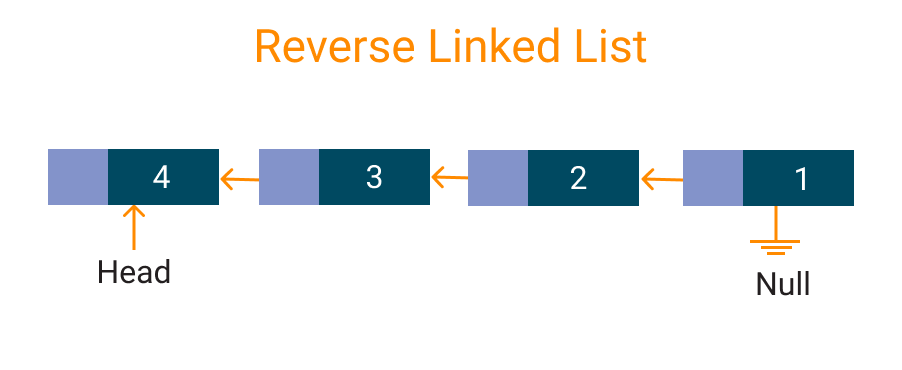
Switch Linked List
There can be two ways to deal with tackling this issue, coming up next are simply the clues, taking a stab at taking care of the issue without help from anyone else and afterward head over to the following area to observe the arrangement and C++ code.
Hints
Think about an iterative way to deal with tracking down the switched list in a solitary pass.
Or then again, think about a recursive way to deal with track down the turned around list in a solitary pass.
Since you have had a go at tackling the issue yourself given the two kinds of ways to deal with taking care of this issue, how about we examine both the methodologies individually:
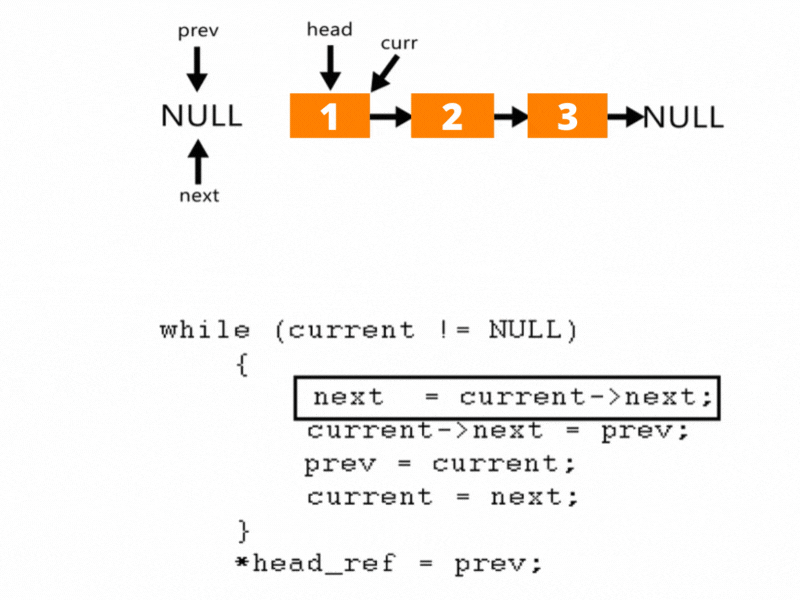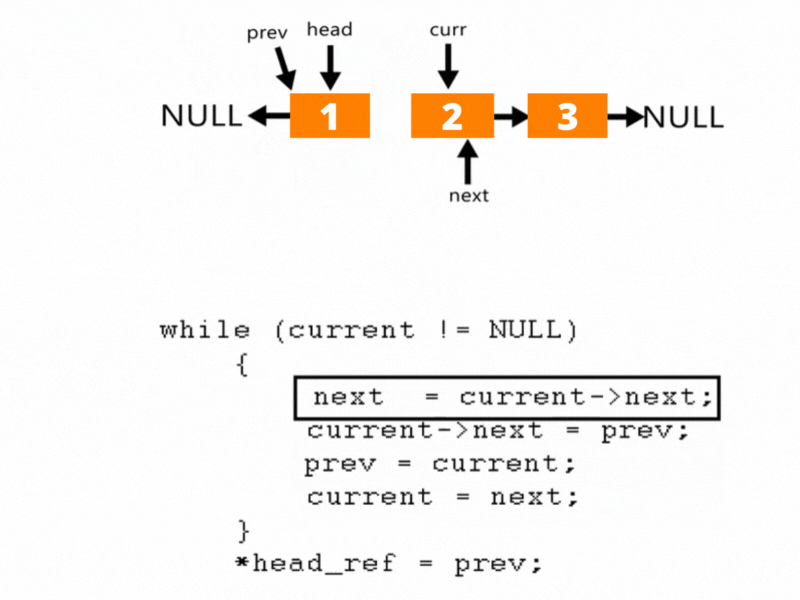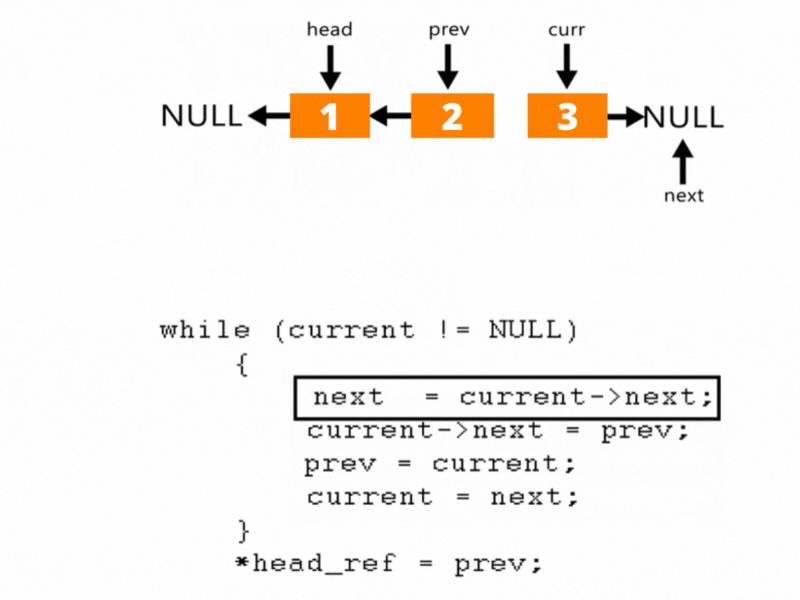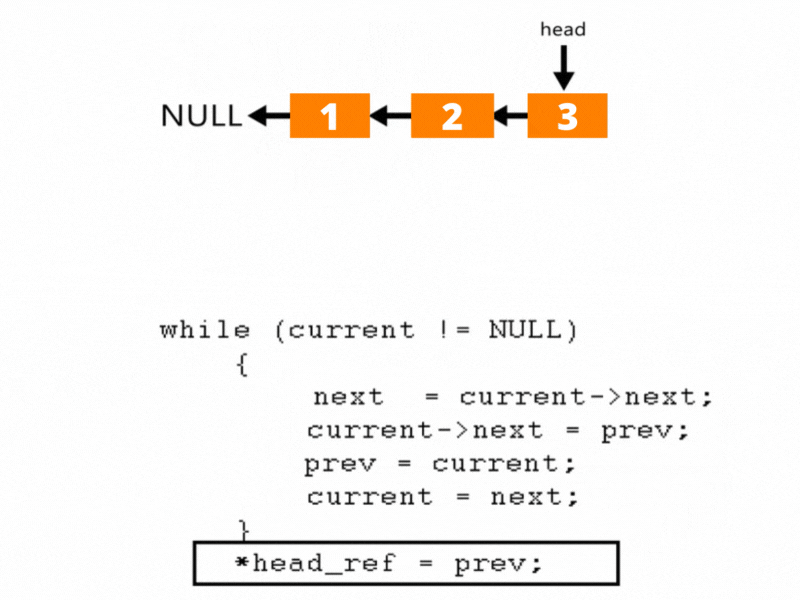
Iterative Solution for Reversing a Linked List
On the off chance that the connected rundown has just one or no component, then, at that point, we return the current rundown for what it’s worth. What’s more on the off chance that there are at least two components, then, at that point, we can execute an iterative arrangement utilizing three-pointers
We will make a capacity to invert the connected rundown taking reference to the head hub and as the main contention and return the top of the new connected rundown:
Stage 1: Define three hubs one with the reference to the head hub and name it current, and name the other two hubs temp and prev pointers as NULL.
Stage 2: Using some time circle we will cross the connected rundown once until the following pointer doesn’t become NULL.
Stage 3: While repeating, we play out the accompanying activities:
temp = current->next;
current->next = prev;
prev = current;
current = temp;
We relegate the temp hub to the following of the current hub and afterward turn around the connection by allocating the current->next to the past hub. And afterward, increase the past hub to the current hub and afterward the current hub to the temp hub.
And afterward we at last return the head hub.
Iterative Implementation
The iterative implementation of reversing a linked list in c++ follows:-
#include<bits/stdc++.h>
using namespace std;
struct node {
int data;
struct node *next;
};
// To create a demo we have to construct a linked list and this
// function is to push the elements to the list.
void push(struct node **head_ref, int data) {
struct node *node;
node = (struct node*)malloc(sizeof(struct node));
node->data = data;
node->next = (*head_ref);
(*head_ref) = node;
}
// Function to reverse the list
void reverse(struct node **head_ref) {
struct node *temp = NULL;
struct node *prev = NULL;
struct node *current = (*head_ref);
while(current != NULL) {
temp = current->next;
current->next = prev;
prev = current;
current = temp;
}
(*head_ref) = prev;
}
// To check our program
void printnodes(struct node *head) {
while(head != NULL) {
cout<<head->data<<" ";
head = head->next;
}
}
// Driver function
int main() {
struct node *head = NULL;
push(&head, 0);
push(&head, 1);
push(&head, 8);
push(&head, 0);
push(&head, 4);
push(&head, 10);
cout << "Linked List Before Reversing" << endl;
printnodes(head);
reverse(&head);
cout << endl;
cout << "Linked List After Reversing"<<endl;
printnodes(head);
return 0;
}
Output:
Linked List Before Reversing
10 4 0 8 1 0
Linked List After Reversing
0 1 8 0 4 10
Time complexity:
O(N) because we iterate through each element at least once.
Space complexity:
O(1) because no extra space was used here.
Recursive answer for Reversing a Linked List
The main thing to recall in this methodology is that the recursive methodology utilizes a stack. The compiler distributes stack memory later each recursive call, and this arrangement can run out of memory if there should arise an occurrence of extremely colossal connected records (consider billions components).
Turning around a connected rundown C++
We recursively emphasize to every hub in the rundown until we arrive at the last hub and return the new head. We need to take note that the last hub in this methodology will turn into the new top of the rundown. On the return way, every hub will affix itself to the furthest limit of the somewhat turned around connected rundown.
Recursive Implementation
The recursive execution of turning around a connected rundown in c++ follows:-
#include
using namespace std;
struct Node {
int data;
struct Node* next;
Node(int data)
{
this->data = data;
next = NULL;
}
};
struct LinkedList {
Node* head;
LinkedList()
{
head = NULL;
}
Node* reverse(Node* head)
{
if (head == NULL || head->next == NULL)
return head;
// Recursive call
Node* rest = reverse(head->next);
head->next->next = head;
head->next = NULL;
return rest;
}
void print()
{
struct Node* temp = head;
while (temp != NULL) {
cout << temp->data << " ";
temp = temp->next;
}
}
void push(int data)
{
Node* temp = new Node(data);
temp->next = head;
head = temp;
}
};
int main()
{
LinkedList ll;
ll.push(320);
ll.push(34);
ll.push(315);
ll.push(385);
cout << "Linked List Before Reversing\n";
ll.print();
ll.head = ll.reverse(ll.head);
cout << "\nLinked List After Reversing \n";
ll.print();
return 0;
}
Output:
Linked List Before Reversing
385 315 34 320
Linked List After Reversing
320 34 315 385
Time Complexity:
O(N) because we iterate through each element at least once.
Space complexity:
O(N) because we create a recursive stack each time we call the reverse function recursively.
Also Read: How to Sort a LinkedList in Java?