Table of Contents
Introduction to Delta-Wye Transformation
How to Perform delta-wye Transformation? Sometimes when we are encountering certain resistor based circuit analysis, we come across some special cases where we cannot solve the circuit linearly by simply using the basic circuit analysis strategies. These type of problems occasionally appear when we are dealing with complex circuitry or in more simplified words, a three-phase circuit network. The solution of these problems cannot be extracted by simply using the nodal-mesh analysis. Thus for the solution of these particular type of problems, we introduce the WYE-DELTA TRANSFORMATION
Wye-Delta Transformation
The wye-delta or commonly written as Y-Δ is a mathematical technique which is commonly used by engineers all across the globe for simple analysis of a complex electrical circuit. The name of this method came into being because of the formation of circuit. If one closely observes the circuit, it will somehow resemble the shape of resistor connection like Y or Δ. Δ is a Greek capital letter which is used here primarily because of its closed figure that resemble the connections of resistors. This form of transformation was first explained by Arthur Edwin Kennelly in 1899 when he published his circuit transformation theory. As mentioned earlier, it is widely used for the analysis of three-phase electric power circuits.
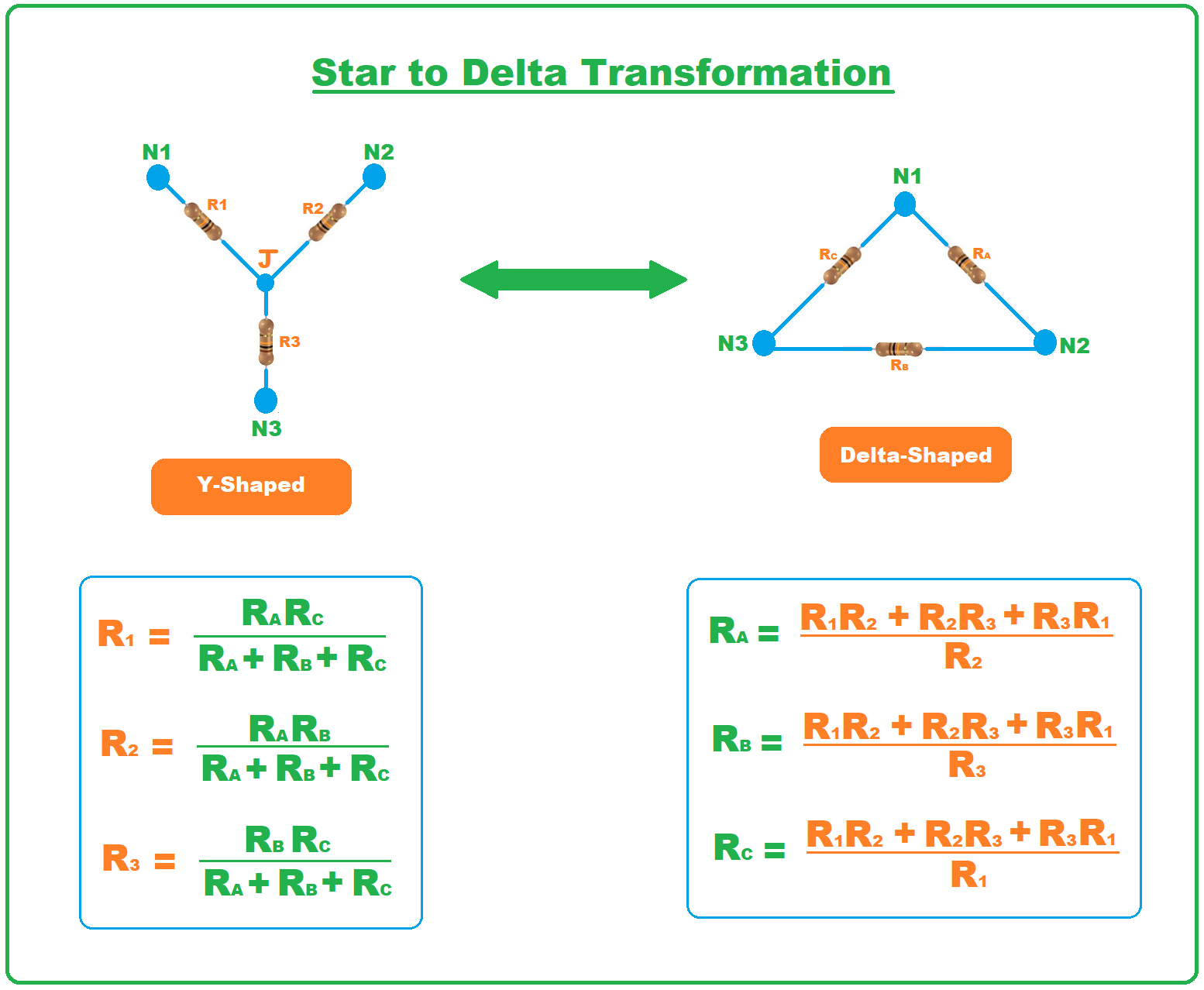
Basic Y-Δ Transformation
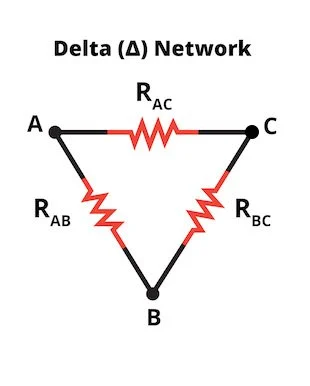
If we dig deeper into understanding of Y-Δ transform, we see that in Δ form of circuit, two resistors are attached from one node. Thus we can say that the first node, both resistors are in a form of parallel combination with each other. But at the end of each resistor, both of them are connected to another resistor that forms a closed triangle typed shape. Three total terminal are included here. One terminal at first node and the other two terminals at the joining point of both resistors with the third resistor.
While taking the Y formation into consideration, we come across a circuit with three terminals and just one node. First we get a terminal of one end of resistor, then moving along the resistor, we see a node where the ends of all three resistors meet. This is the grand node. Form here the other two resistors move along their way towards the 2nd and 3rd terminals respectively.

EQUATIONS FOR Y- $\triangle$ TRANSFORMATION
These equations are used for transforming values of resistances in $Y$ formation to their new formation i.e. $\Delta$ formation. The general concept is to evaluate the resistance $R_{\Delta}$ in the $\Delta$ circuit by computing the rest of resistances of $Y$ formation
$$
\boldsymbol{R}_{\Delta}=\frac{\boldsymbol{R}_{\boldsymbol{P}}}{\boldsymbol{R}_{\text {OPPOSITE }}}
$$
Where $\boldsymbol{R}_P$ is the sum of product of all the paired resistances present in Y circuit. And $\boldsymbol{R}_{\text {OPPOSITE }}$ is the resistance in $Y$ circuit which is opposite to the resistance in $R_{\Delta}$. The formulas for the individual edges resistances are
$$
\begin{aligned}
R_A=& \frac{R_1 R_2+R_2 R_3+R_3 R_1}{R_1} \\
R_B &=\frac{R_1 R_2+R_2 R_3+R_3 R_1}{R_2} \\
R_C &=\frac{R_1 R_2+R_2 R_3+R_3 R_1}{R_3}
\end{aligned}
$$
EQUATIONS FOR $\triangle-Y$ TRANSFORMATION
These equations are used for transforming the values of resistances in $\Delta$ formation to $Y$ formation that will be their new formation. The general concept of these equations is to calculate the value of $\boldsymbol{R}_Y$ at the terminal nodes of their new formation by utilizing the resistances of $\Delta$ formation.
$$
R_Y=\frac{R \ddot{R}}{\sum R_{\Delta}}
$$
Where $R_{\Delta}$ are the total resistances of $\Delta$ circuit. The specified equations for this $\Delta$-Y transform are
$$
\begin{aligned}
\boldsymbol{R}_1 &=\frac{\boldsymbol{R}_B \boldsymbol{R}_C}{\boldsymbol{R}_A+\boldsymbol{R}_B+\boldsymbol{R}_C} \\
\boldsymbol{R}_2 &=\frac{\boldsymbol{R}_A \boldsymbol{R}_C}{\boldsymbol{R}_A+\boldsymbol{R}_B+\boldsymbol{R}_C} \\
\boldsymbol{R}_3 &=\frac{\boldsymbol{R}_A \boldsymbol{R}_B}{\boldsymbol{R}_A+\boldsymbol{R}_B+\boldsymbol{R}_C}
\end{aligned}
$$
Example of wye-delta Transformation
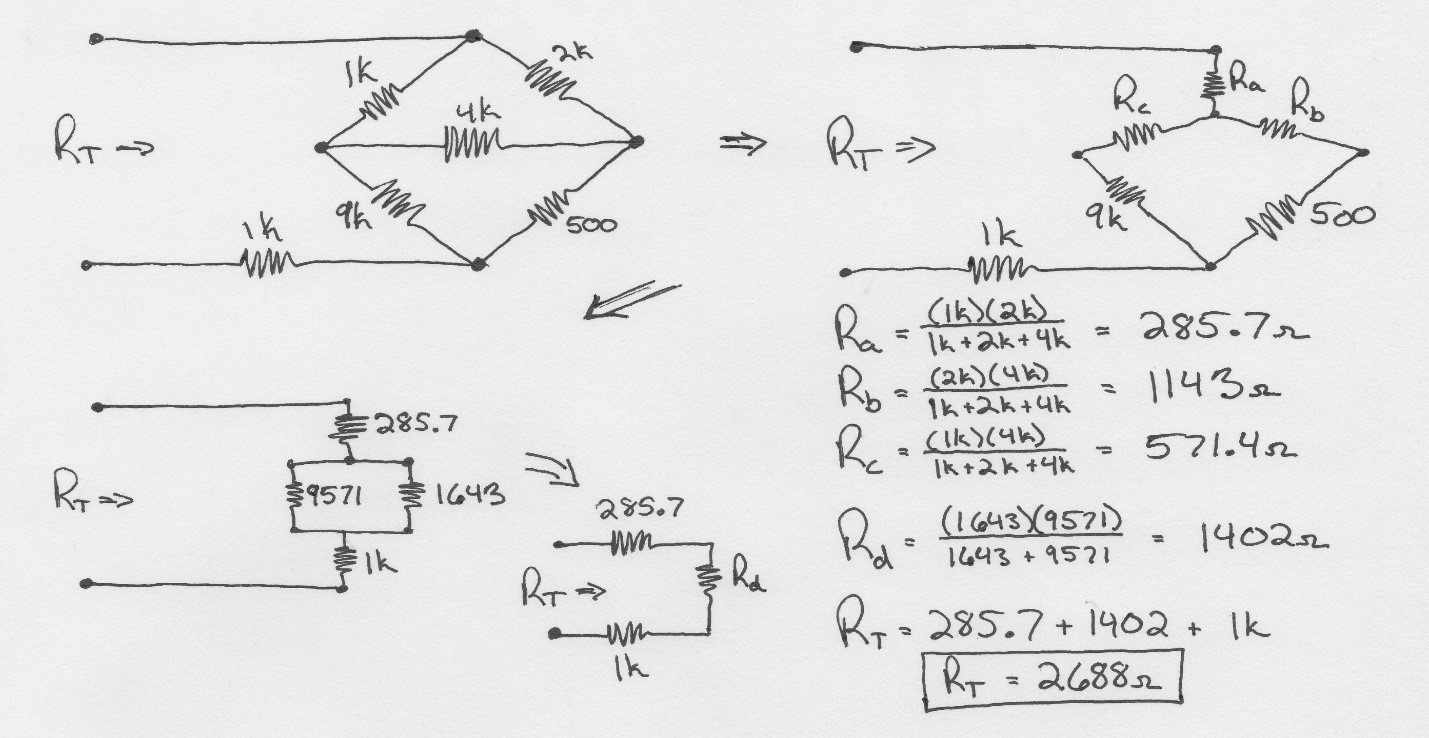

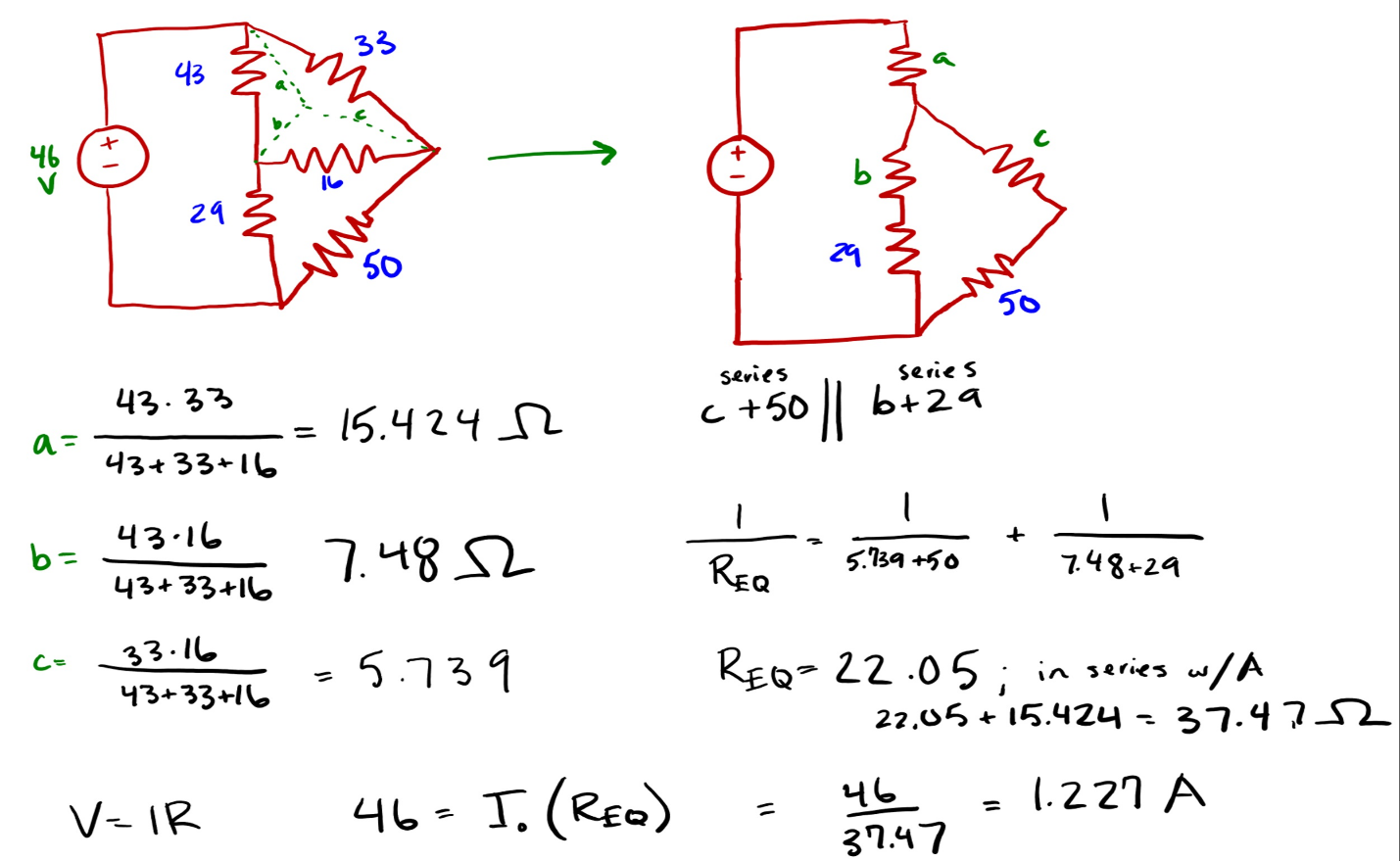
Also read here: