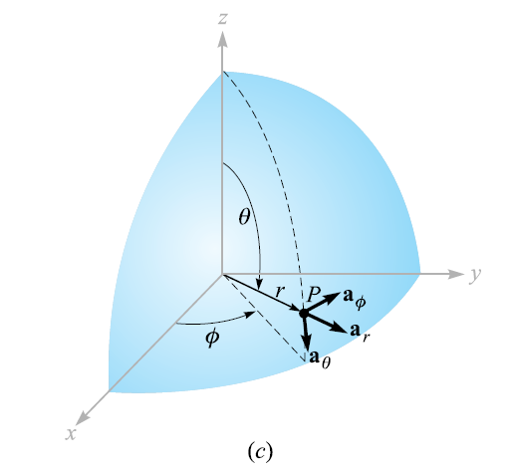
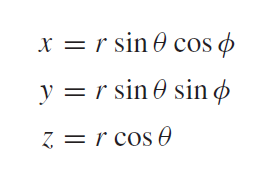What is the spherical coordinate system?
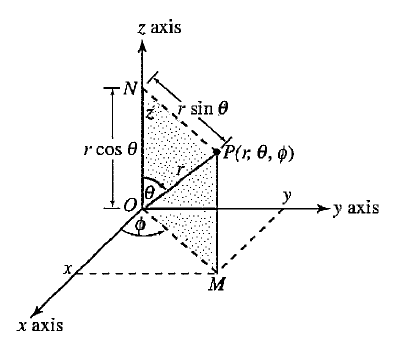
What is the spherical coordinate system? A point P in space in spherical coordinates is uniquely represented in terms of r,θ,φ, where r is the radial distance from O to P, θ in the angle that r makes with the positive z-axis, and φ is the angle between the positive xz and OMPN planes and it varies from 0 to 2π. An oscillating charge produces the radiations of spherical pattern.
The surface r = constant is a sphere,
The surface θ = constant is a cone,
(two surfaces, cone and sphere, are everywhere perpendicular along their intersection, which is a circle of radius r sin θ)
The surface φ = constant is a plane passing through the θ = 0 line (or the z axis).
The projection of r on x-plane is OM=r sinθ.”The positive direction of ” θ” is from the positive z-axis, where its value is 0, towards the negative z-axis, where its value is π. So ” θ” varies from 0 to π. “However, 0≤r≤∞.

These three surfaces are mutually perpendicular to each other as it can be seen in the figure below.
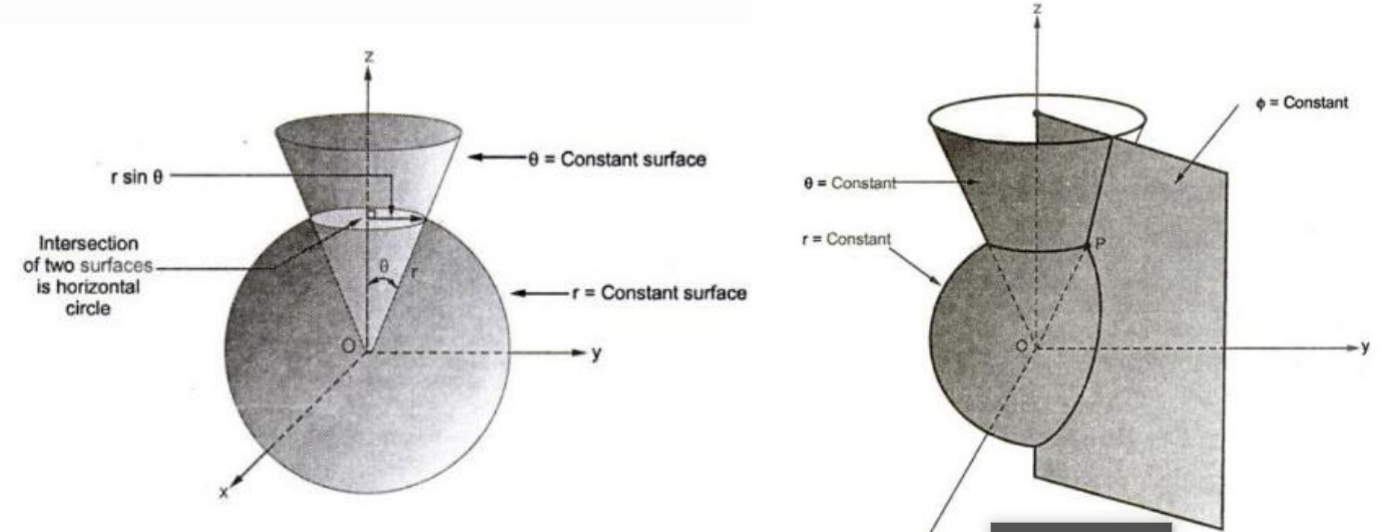
We consider any point as the intersection of three mutually perpendicular surfaces—a sphere, a cone, and a plane—each oriented in the manner just described.
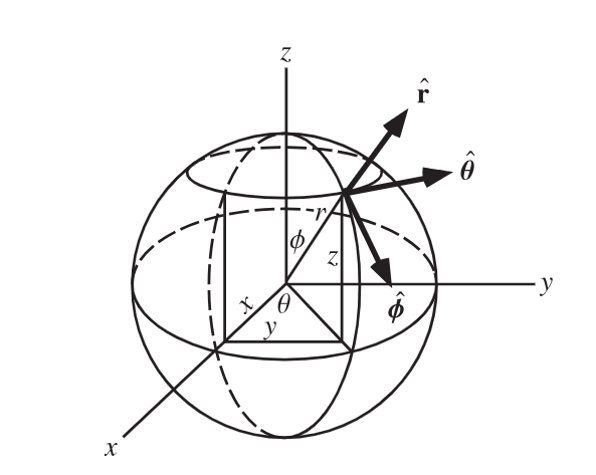
Unit Vectors in Spherical Coordinate System
The unit vector ar is directed radially outward, normal to the sphere r = constant, and lies in the cone θ = constant and the plane φ = constant.
The unit vector aθ is normal to the conical surface, lies in the plane, and is tangent to the sphere.
The third unit vector aφ is the same as in cylindrical coordinates, being normal to the plane and tangent to both the cone and the sphere.
Relation Between Spherical and Rectangular Coordinate System
The relation between spherical and rectangular coordinate systems can be found using the following formulas.
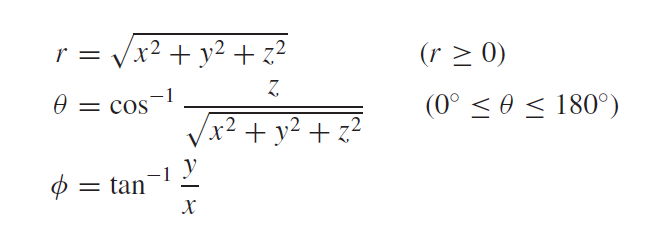
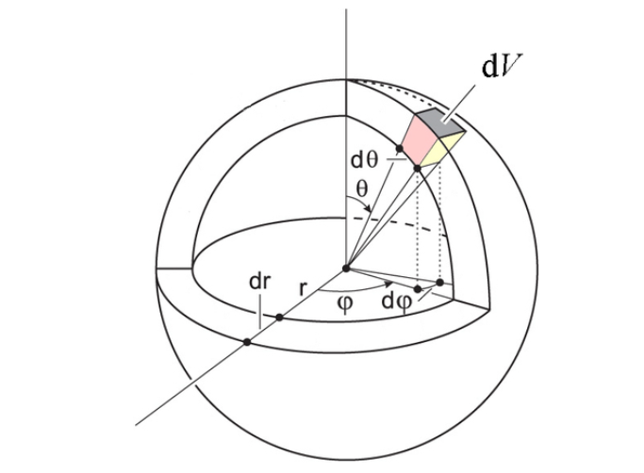
Differential Element in Spherical Coordinate System
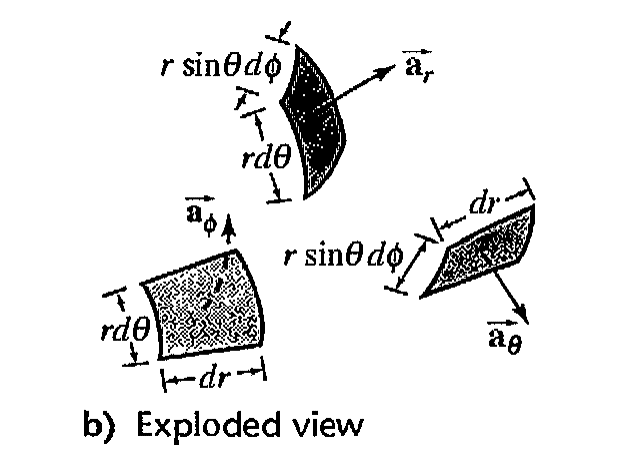
A differential volume element may be constructed in spherical coordinates by increasing r , θ, and φ by dr, dθ, and dφ, as shown in figure below:
Area of Differential Surfaces
The surfaces have areas of :
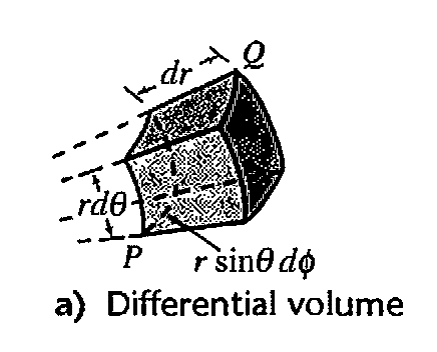
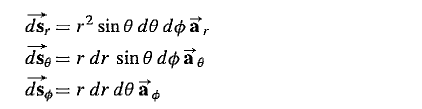
Electromagnetic Field Theory lecture 3
Video Lecture of Spherical Coordinate System
The follow lecture describes the complete detail of spherical coordinate systems.
Relation between spherical and cartesian coordinates systems
https://www.youtube.com/watch?v=zcoOkG7ppV0
Also read here
https://eevibes.com/electromagnetic-field-theory/what-is-the-cylindrical-coordinate-system/